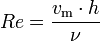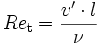Rezahl

Die Reynolds-Zahl (Formelzeichen: $R e$ ) ist eine nach dem Physiker Osborne Reynolds benannte dimensionslose Kennzahl. Sie wird in der Strömungslehre verwendet und stellt das Verhältnis von Trägheits- zu Zähigkeitskräften dar (bzw. das Verhältnis von spezifischer Impulskonvektion zu Impulsdiffusion im System). Für eine ideale Flüssigkeit ohne Viskosität ist das Verhältnis unendlich.

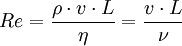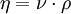
$Re = \frac{\rho \cdot v \cdot L}{\eta} = \frac{v \cdot L}{\nu}$ mit: $\eta = \nu \cdot \rho$

Die einzelnen Formelzeichen stehen für folgende Größen:

$ρ$ – charakteristische Dichte des Anwendungsfalles ( $kg\ m^{-3}$ ).
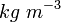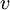$\!\ v$ – Betrag einer für den Anwendungsfall charakteristischen Strömungsgeschwindigkeit ( $m\ s^{-1}$ ),
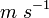$L$ – charakteristische Länge des Anwendungsfalles ( $m$ ),
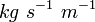$η$ – charakteristische dynamische Viskosität des Anwendungsfalles ( $kg\ s^{-1}\ m^{-1}$ ),
$ν$ – charakteristische kinematische Viskosität des Anwendungsfalles ( $m^{2}\ s^{-1}$ ),

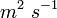Überschreitet die Reynolds-Zahl einen (problemabhängigen) kritischen Wert ( $R e krit$ ), wird eine bis dahin laminare Strömung anfällig gegen kleinste Störungen. Entsprechend ist für $R e > R e krit$ mit einem Umschlag, der so genannten Transition, von laminarer in turbulente Strömung zu rechnen.

In der Magnetohydrodynamik wird ebenfalls eine Reynolds-Zahl definiert: die magnetische Reynolds-Zahl.

Anwendungen

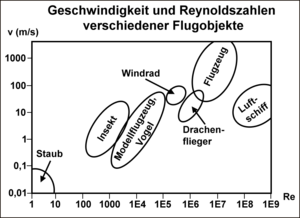
Geschwindigkeiten und Reynolds-Zahlen einiger Flugobjekte

Das Diagramm rechts vergleicht Geschwindigkeiten und zugehörige Reynolds-Zahlen einiger Flugobjekte. Beispielsweise sind die Reynolds-Zahlen von Luftschiffen höher als die von Flugzeugen. Sie fahren zwar langsamer, sind aber deutlich größer.

Die Reynolds-Zahl ist eine wichtige Größe innerhalb der Ähnlichkeitstheorie. Will man zum Beispiel ein verkleinertes Modell eines Flugzeuges in einem Windkanal untersuchen, so muss der Wert der Reynolds-Zahl von Original und Modell gleich sein, um ein ähnliches Strömungsfeld zu erhalten. Entsprechend muss bei einem um einen Faktor $f$ verkleinerten Modell das Verhältnis $\tfrac{v}{\nu}$ um den Faktor $f$ erhöht werden. Da die Maximalgeschwindigkeit begrenzt ist, senkt man in Kryo-Windkanälen zusätzlich die Viskosität der Luft durch Kühlung und erhöht dadurch gleichzeitig die Luftdichte. Auf diese Weise sind Reynolds-Zahlen bis zu 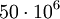$50 \cdot 10^6$ in Probenkammern von zwei Metern Durchmesser erreichbar. Dieses Vorgehen ist allerdings sehr teuer, da hier meist mit flüssigem Stickstoff der Kanal mitsamt Modell abgekühlt werden muss. Beim Abkühlen muss darauf geachtet werden, dass sich keine Vereisungen bilden. Eine weitere Erhöhung der Reynolds-Zahl kann auch durch die Erhöhung des statischen Druckes erreicht werden.

Staubkörner sind sehr klein. Wenn sie durch die Luft fallen, haben sie eine ähnliche niedrige Reynolds-Zahl wie eine Stahlkugel, die in ein Glas Honig fällt. Sie bewegt sich laminar (d. h. ohne Wirbelbildung) durch das Fluid. Ein Körper, der sich durch Wasser bewegt, hat bei gleicher Geschwindigkeit eine ca 15fach höhere Reynoldszahl, als wenn er sich durch Luft bewegt. Zwar ist die dynamische Viskosität von Wasser ca. 50mal höher als die von Luft, jedoch ist auch die Dichte um das 800fache höher, so dass am Ende eine höhere Reynoldszahl resultiert:

Substanz	rel. dynamische Viskosität	rel. Dichte	rel. Dichte/Viskosität
Wasser	1	1	1
Luft	0,02	0,0013	0,0013/0,02 = 0,065 ≈ 1/15

Mikroorganismen schwimmen bei Reynoldszahlen $10 - 5$ bis $10 - 2$ , so dass Inertialkräfte vernachlässigbar sind. Ein Beispiel: Hörten die Geißeln des Bakteriums E. coli auf zu schlagen, käme dieser Schwimmer bereits nach weniger als einem Atomdurchmesser zum Stehen.

Beispiele

Rohrströmung

Bei Rohrströmungen werden als charakteristische Größen üblicherweise der Innendurchmesser $L = d$ , der Betrag der über den Querschnitt gemittelten Geschwindigkeit $v = v m$ und die Viskosität des Fluids $ν$ verwendet.

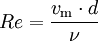$Re = \frac{v_{\rm m} \cdot d}{\nu}$ .

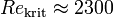Es gilt dann: $Re_{\rm krit} \approx 2300$ .

Zu beachten ist, dass die kritische Reynoldszahl $R e krit$ nicht exakt den Übergang von einer laminaren zu einer turbulenten Strömung charakterisiert. Es ist in Experimenten gelungen, laminare Rohrströmungen mit $R e > 10000$ zu erzeugen, ohne dass die Strömung turbulent geworden ist. Die kritische Reynoldszahl ist jedoch geeignet als Maß für den umgekehrten Übergang: Wenn die Strömung im Rohr verlangsamt wird, kann man bei Re<2300 von einer laminaren Strömung ausgehen.

Die kritische Reynoldszahl $R e krit$ , die den Übergang zwischen turbulenter und laminarer Strömung markiert, ist nicht nur abhängig von der Geometrie des Anwendungsfalles, sondern auch von der Wahl der charakteristischen Masse. Wird zum Beispiel der Rohrradius statt dem Durchmesser der Strömung als charakteristisches Längenmass einer Rohrströmung gewählt, halbiert sich der Zahlenwert $R e krit$ , der dasselbe aussagen soll. Da die kritische Reynoldszahl ein Wert ist, der keinen blitzartigen Umschlag, sondern einen breiten Übergangsbereich der Strömungsverhältnisse markiert, ist der üblicherweise verwendete Zahlenwert nicht 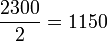$\frac{2300 }{2} = 1150$ sondern wird auf 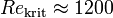$Re_{\rm krit} \approx 1200$ gerundet.

Gerinneströmung

Bei Gerinneströmungen werden als charakteristische Größen die Fließtiefe $L = h$ , der Betrag der mittleren Fließgeschwindigkeit über den durchflossenen Querschnitt $v = v m$ und die Viskosität des Fluids $ν$ verwendet.

$Re = \frac{v_{\rm m} \cdot h}{\nu}$

Beurteilung einer turbulenten Strömung

Um den Turbulenzgrad zu charakterisieren, kann die Reynolds-Zahl auch mit turbulenzbezogenen Größen gebildet werden (turbulente Reynolds-Zahl $R e t$ ). Als charakteristische Größen werden dann bspw. die Varianz der Geschwindigkeit $v = v'$ und das integrale Längenmaß L = l der Strömung verwendet. Hinzu kommt die (molekulare) Viskosität des Fluids $ν$ .

$Re_{\rm t} = \frac{v' \cdot l}{\nu}$

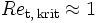Es gilt dann: $Re_{\rm t,\, krit}\approx 1$ .

Siehe auch

Quellen

Weblinks

Wikimedia Foundation.

Игры ⚽ Поможем написать реферат

Academic dictionaries and encyclopedias

Rezahl

Inhaltsverzeichnis

Anwendungen