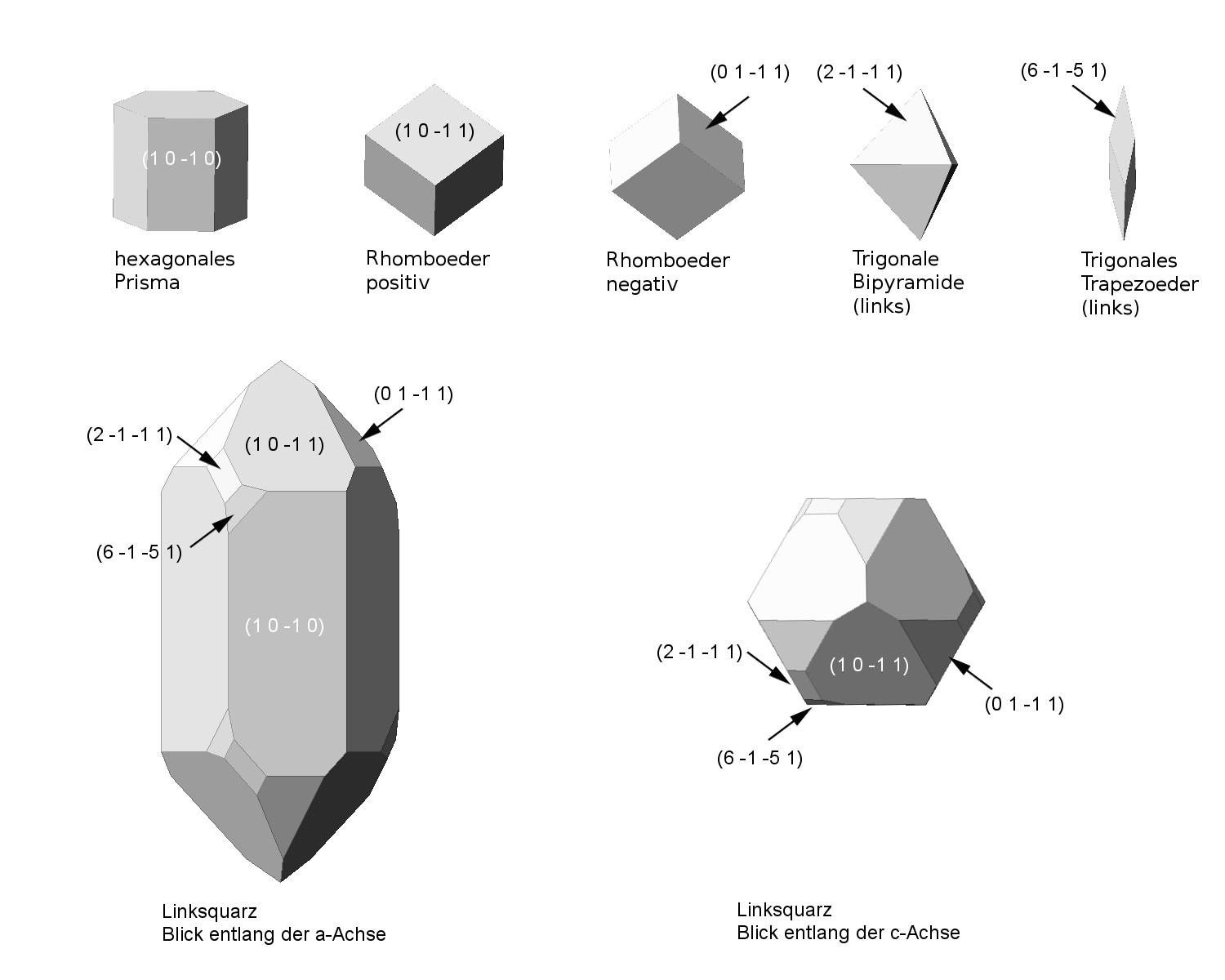
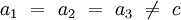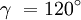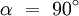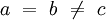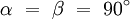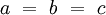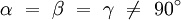- Rhomboedrisch
-
Das Trigonale Kristallsystem gehört zu den sieben Kristallsystemen in der Kristallographie. Es ist eng verwandt mit dem hexagonalen Kristallsystem, da beiden das gleiche vierachsige Achsenkreuz zugrunde liegt. Im Fall einer rhomboedrischen Zentrierung des Bravais-Gitters, spricht man auch von einem rhomboedrischen Kristallsystem (s.u.), was vor allem im englischen Sprachgebrauch üblich ist.
Inhaltsverzeichnis
Achsenkreuz des trigonalen Kristallsystems
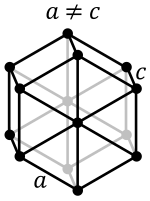
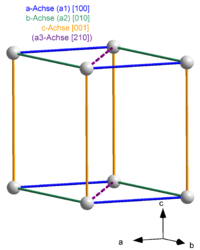 Die trigonale (hexagonale) Elementarzelle entspricht einem Drittel der links dargestellten Abbildung und enthält alle notwendigen Informationen
Die trigonale (hexagonale) Elementarzelle entspricht einem Drittel der links dargestellten Abbildung und enthält alle notwendigen InformationenDem trigonalen und hexagonalen Kristallsystem liegt folgendes Achsenkreuz zugrunde:
- Drei gleichlange Achsen a1, a2 und a3, die in einer Ebene liegen und sich in einem Winkel (γ) von jeweils 120° schneiden.
- Die vierte Achse c ist ungleich lang wie a1, a2 und a3, und steht senkrecht (α = 90°) auf der Ebene, die die drei a-Achsen aufspannen.
Die Elementarzelle eines Kristalls im trigonalen Kristallsystem lässt sich vollständig mit folgenden Gitterparametern beschreiben:
Analog zu den anderen Kristallsystemen wird für gewöhnlich die a2-Achse als b-Achse angegeben. Die a3-Achse wird bei den Gitterparametern nicht angegeben, da ihre Orientierung und damit auch ihre Winkel durch die Lage der a-, b- und c-Achse festgelegt ist.
Für das trigonale Kristallsystem, wie auch für das hexagonale Kristallsystem, wird daher folgende Definition verwendet:
Bei den Gitterparametern im trigonalen oder hexagonalen Kristallsystem wird daher nur die a- und c-Achse angegeben, da die restlichen Parameter durch die Definition festgelegt sind.
Die Unterscheidung zwischen trigonalem und hexagonalem Kristallsystem erfolgt nur durch die auftretenden Symmetrieelemente der Kristallklasse beziehungsweise Raumgruppe der Kristallstruktur. Treten nur dreizählige Symmetrieachsen (Hermann-Mauguin-Symbol „3“, das heißt Vervielfältigung eines Teilchens durch Drehung um 120°) beziehungsweise dreizählige Drehinversionsachsen (Symbol „
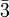 “, das heißt Vervielfältigung eines Teilchens durch Drehung um 120° und anschließende Punktspiegelung) parallel der kristallographischen c-Achse auf, spricht man von der Zugehörigkeit zum trigonalen Kristallsystem. Im hexagonalen Kristallsystem treten dagegen sechszählige Symmetrieachsen oder Drehinversionsachsen auf (Symbol „6“ beziehungsweise „
“, das heißt Vervielfältigung eines Teilchens durch Drehung um 120° und anschließende Punktspiegelung) parallel der kristallographischen c-Achse auf, spricht man von der Zugehörigkeit zum trigonalen Kristallsystem. Im hexagonalen Kristallsystem treten dagegen sechszählige Symmetrieachsen oder Drehinversionsachsen auf (Symbol „6“ beziehungsweise „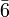 “, Vervielfältigung eines Teilchens durch Drehung um 60°, im zweiten Fall anschließende Punktspiegelung).
“, Vervielfältigung eines Teilchens durch Drehung um 60°, im zweiten Fall anschließende Punktspiegelung).Rhomboedrische Zentrierung
 Rhomboedrische Zentrierung am Beispiel von Korund
Rhomboedrische Zentrierung am Beispiel von KorundWährend im hexagonalen Kristallsystem nur eine primitive Zentrierung des Bravais-Gitters auftreten kann, kann bei trigonaler Symmetrie das Bravais-Gitter auch rhomboedrisch zentriert sein. Die Elementarzelle eines Kristalls mit rhomboedrischen zentriertem Gitter kann wie folgt beschrieben werden:
Die rhomboedrische Aufstellung kann dann angewendet werden, wenn in der primitiven trigonalen Zelle auf den Koordinaten x = 1/3, y = 2/3, z = 2/3 und x = 2/3, y = 1/3, z = 1/3 die gleichen Teilchen wie auf den Ecken auftreten, wodurch zwei weitere Gitterpunkte entstehen. Die dreizählige Symmetrieachse befindet sich in der rhomboedrischen Zelle entlang der langen Raumdiagonalen, das Volumen der rhomboedrischen Zelle beträgt ein Drittel der trigonal primitiven Zelle. Eine Elementarzelle mit rhomboedrischer Metrik kann daher immer auch als trigonal primitive Zelle beschrieben werden. Umgekehrt kann nicht jede trigonal primitive Zelle rhomboedrisch aufgestellt werden, genau dann nicht, wenn die beiden oben beschriebenen Gitterpunkte fehlen. Die rhomboedrische Zelle kann auch als entlang der Raumdiagonalen gestreckter beziehungsweise gestauchter Würfel angesehen werden, umgekehrt bildet der Würfel einen Spezialfall eines Rhomboeders mit α = β = γ = 90°.
Kristallklassen des trigonalen Kristallsystems
Kristallklasse Schönflies-Symbol Hermann-Mauguin-Symbol Beispiel trigonal-pyramidal C3 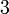
Carlinit (Tl2S) rhomboedrisch C3i 
Dioptas, Dolomit, Ilmenit trigonal-trapezoedrisch D3 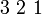 oder
oder 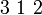
Cinnabarit, Quarz, Selen, Tellur ditrigonal-pyramidal C3v 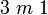 oder
oder 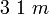
Pyrargyrit, Turmalingruppe ditrigonal-skalenoedrisch D3d 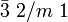 oder
oder 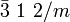
Antimon, Arsen, Bismut, Calcit, Hämatit, Korund Kristallformen des trigonalen Kristallsystems
Literatur
- W. Borchardt-Ott: Kristallographie. 6. Auflage. Springer Verlag, Berlin 2002, ISBN 3-540-43964-1
- W. Massa: Kristallstrukturbestimmung. 3. Auflage. Teubner Verlag, Stuttgart 2002, ISBN 3-519-23527-7
- M. Okrusch, S. Matthes: Mineralogie. 7. Auflage. Springer Verlag, Berlin 2005, ISBN 3-540-23812-3
Weblinks
Wikimedia Foundation.