- Rieszraum
-
Riesz-Raum berührt die Spezialgebiete
ist Spezialfall von
Ein Riesz-Raum (zu Ehren von Frigyes Riesz) ist ein Vektorraum mit einer Verbandsstruktur, die so beschaffen ist, dass sich die lineare und die Verbandsstruktur vertragen.
Inhaltsverzeichnis
Definition
Sei
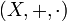 ein
ein  -Vektorraum und
-Vektorraum und 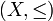 eine teilweise geordnete Menge.
eine teilweise geordnete Menge.Dann heißt
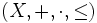 ein Riesz-Raum wenn folgende Axiome erfüllt sind:
ein Riesz-Raum wenn folgende Axiome erfüllt sind:- Für alle
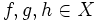 gilt:
gilt: 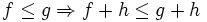 .
. - Für alle
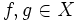 gilt:
gilt: 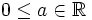 und
und 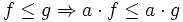 .
. 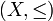 ist ein Verband.
ist ein Verband.
Anmerkungen
- 1. und 2. bedeuten
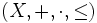 ist ein geordneter Vektorraum.
ist ein geordneter Vektorraum. - Bei der Formulierung von 2. ist zu beachten, dass
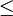 sich sowohl auf
sich sowohl auf  , als auch auf X bezieht, aus dem Zusammenhang ist meistens klar, welche Ordnungsrelation gemeint ist, so dass üblicherweise auf zusätzliche Indizes verzichtet wird.
, als auch auf X bezieht, aus dem Zusammenhang ist meistens klar, welche Ordnungsrelation gemeint ist, so dass üblicherweise auf zusätzliche Indizes verzichtet wird. - 2. lässt sich auch durch die schwächere Forderung
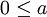 und
und 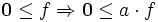 ersetzen.
ersetzen. - Bezeichnen
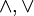 die Verbandsoperationen, so ist es Konvention, dass
die Verbandsoperationen, so ist es Konvention, dass 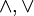 stärker binden, als
stärker binden, als 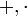 (Klammerregel).
(Klammerregel).
Erste Eigenschaften
Für
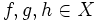 und
und 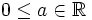 gelten folgende Rechenregeln:
gelten folgende Rechenregeln: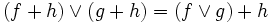 und
und 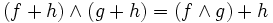
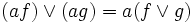 und
und 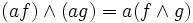
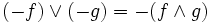 und
und 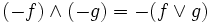
- Sei
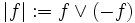 für
für 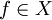 .
.
- Dann gilt
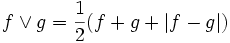 und
und 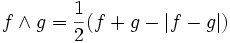 .
.
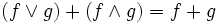 und
und 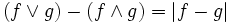
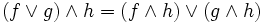 und
und 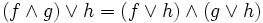
- Dies bedeutet jeder Riesz-Raum ist ein distributiver Verband.
Beispiele
- Die reellen Zahlen
 mit der üblichen Anordnung
mit der üblichen Anordnung 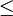 bilden einen Riesz-Raum.
bilden einen Riesz-Raum. - Der
 mit komponentenweiser Anordnung bildet einen Riesz-Raum.
mit komponentenweiser Anordnung bildet einen Riesz-Raum. - Die Menge der reellen Zahlenfolgen
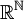 mit komponentenweiser Anordnung bildet einen Riesz-Raum.
mit komponentenweiser Anordnung bildet einen Riesz-Raum. - Die Menge der reellen Nullfolgen c0 mit komponentenweiser Anordnung bildet einen Riesz-Raum.
- Für
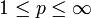 ist lp mit komponentenweiser Anordnung ein Riesz-Raum.
ist lp mit komponentenweiser Anordnung ein Riesz-Raum. - Die Menge der beschränkten reellen Folgen
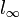 mit komponentenweiser Anordnung bildet einen Riesz-Raum.
mit komponentenweiser Anordnung bildet einen Riesz-Raum. - Die Menge der stetigen Funktionen
![\mathcal{C}[a,b]](/pictures/dewiki/52/49267b1a71300e5d3b38039ddce0bd73.png) auf einem Intervall [a,b] bildet mit punktweiser Anordnung einen Riesz-Raum.
auf einem Intervall [a,b] bildet mit punktweiser Anordnung einen Riesz-Raum. - Die Menge der stetig differenzierbaren Funktionen
![\mathcal{C}^1[a,b]](/pictures/dewiki/98/b6b5f47d5de969083489a3d7597e3a83.png) auf einem Intervall [a,b] bildet einen geordneten Vektorraum mit der punktweisen Anordnung, aber keinen Riesz-Raum.
auf einem Intervall [a,b] bildet einen geordneten Vektorraum mit der punktweisen Anordnung, aber keinen Riesz-Raum.
- Für alle
Wikimedia Foundation.
