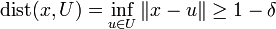Rieszsches Lemma

Das Lemma von Riesz, benannt nach dem ungarischen Mathematiker Frigyes Riesz, ist ein Satz der Funktionalanalysis über abgeschlossene Unterräume von normierten Räumen.

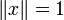Gegeben seien ein normierter Raum X, ein abgeschlossener echter Unterraum U von X und eine reelle Zahl δ > 0. Dann existiert ein Element $x \in X$ mit $\|x\| = 1$, so dass gilt:

$\mathrm{dist}(x,U)=\inf_{u\in U}\|x-u\| \ge 1-\delta$

Ist U endlichdimensional, dann kann δ = 0 gewählt werden. (Es reicht anzunehmen, dass U reflexiv ist.)

Motivation

In einem endlichdimensionalen euklidischen Raum gibt es zu jedem echten Teilraum U einen darauf senkrecht stehenden Einheitsvektor x. Der Abstand eines beliebigen Punktes u aus U zu x beträgt dann mindestens Eins, der Wert Eins wird exakt für u=0 angenommen.

In einem normierten Raum ist der Begriff des „senkrecht Stehens“ nicht definierbar. Insofern ist die Formulierung des Lemmas von Riesz eine sinnvolle Verallgemeinerung. Auch ist es nicht selbstverständlich, dass außerhalb eines Teilraumes noch Vektoren mit positivem Abstand zu diesem existieren.

Beweisskizze

Es gibt einen Punkt w außerhalb der echten Teilmenge U. Da U abgeschlossen ist, muss der Abstand von w zu U positiv sein. Sei ein 0 < δ < 1 vorgegeben (für 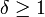$\delta \ge 1$ ist die Aussage trivial) und v ein Punkt in U mit

$\|w-v\|\le \mathrm{dist}(w,U)/(1-\delta)$.

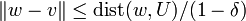Definiere 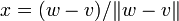$x=(w-v)/\|w-v\|$, d.h. x ist ein Vektor mit Norm 1. Für den Abstand von x zu U gilt

$\mathrm{dist}(x,U)=\frac{\mathrm{dist}(w,U)}{\|w-v\|}\ge\;1-\delta$.

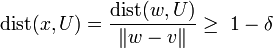Folgerungen

Aus dem Lemma von Riesz folgt, dass jeder normierte Raum, in dem die abgeschlossene Einheitskugel kompakt ist, endlich-dimensional sein muss. Auch die Umkehrung dieses Satzes ist richtig (Kompaktheitssatz von Riesz).