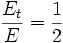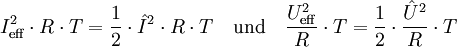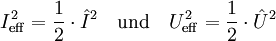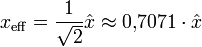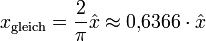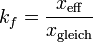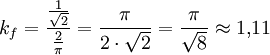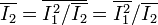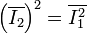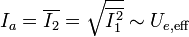- Root mean square
-
Unter dem Effektivwert (Abk: RMS englisch: root mean square) versteht man in der Elektrotechnik den quadratischen Mittelwert eines zeitlich veränderlichen Signals. Intention bei der Einführung des Begriffes ist es, den Wert derjenigen Gleichspannung zu finden, die an einem ohmschen Verbraucher in der gleichen Zeit die gleiche Energie, also dieselbe Leistung, umsetzt. Der Effektivwert hängt sowohl vom Scheitelwert (Amplitude) als auch von der Kurvenform ab.
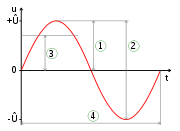 Eine sinusförmige Wechselspannung.
Eine sinusförmige Wechselspannung.
1 = Scheitelwert,
2 = Spitze-Spitze-Wert,
3 = Effektivwert,
4 = PeriodendauerInhaltsverzeichnis
Allgemeines
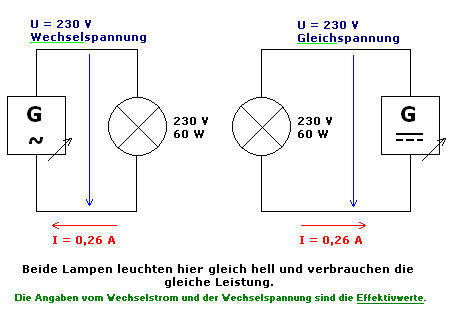
Der häufigste Fall ist die Angabe des Effektivwertes einer Wechselspannung (Effektivspannung), die man aus dem Stromnetz bzw. der Steckdose beziehen kann. Diese sinusförmige Spannung mit einer Frequenz von 50 Hz (in den USA und anderen Ländern auch 60 Hz) mit einem Maximum (Scheitelwert) von etwa 325 V erbringt an einem ohmschen Widerstand (z. B. einem Toaster) im zeitlichen Mittel die gleiche (thermische) Leistung wie eine Gleichspannung von 230 V. Die momentane Spitzenleistung zum Zeitpunkt des Scheitelwertes beträgt jedoch das Doppelte.
Der aufgenommene Strom von Geräten ist oft abweichend von der Spannung nicht gleich- oder sinusförmig, verursacht durch nichtlineare Bauelemente wie Gleichrichterdioden oder Schalttransistoren. Die Stromwärme in Verlustwiderständen ergibt sich jedoch aus seinem Effektivwert, daher muss die Dimensionierung von Leiterquerschnitten den Effektivstrom berücksichtigen.
Mit Hilfe der Effektivwerte von Strom und Spannung lassen sich bei periodischen Spannungsverläufen an ohmschen Verbrauchern die Formeln der Gleichstromtechnik für die Wechselstromtechnik verwenden, wenn die Umrechnungfaktoren der Kurvenformen bekannt sind.
Definition 1
Ist s ein reellwertiges Signal, das von der Zeit t abhängt, und T die Periodendauer des Signals, so heißt
der Effektivwert von s.
Für komplexwertige Signale s berechnet sich der Effektivwert zu
wobei s * das zu s konjugiert komplexe Signal ist.
Lässt sich der Verlauf des Signals nicht ohne weiteres beschreiben, kann man zur Berechnung des Effektivwertes folgendes Näherungsverfahren anwenden.
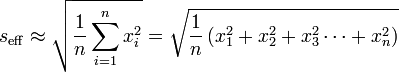 = (Wurzel aus dem Mittelwert der Quadrate)
= (Wurzel aus dem Mittelwert der Quadrate)
wobei Xi Abtast- bzw. Momentanwerte sind, die in einem immer gleichen Abstand Δt während einer Periode T von dem Signal abgelesen werden. Es gilt:
und
Wenn Δt nicht konstant ist gilt.
mit
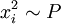 (Momentanleistung)
(Momentanleistung)Definition 2
Der Effektivwert eines Wechselstroms oder einer Wechselspannung entspricht dem Gleichstrom- oder -spannungswert, der in einem ohmschen Widerstand die gleiche Leistung (Wärme) erzeugt wie der über volle Perioden gemittelte Wechselstrom bzw. Wechselspannung.
Spezielle Signalformen
Signal Formel Effektivwert Gleichsignal 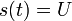
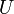
Sinussignal 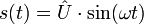
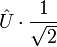
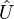 steht dabei für den Maximalwert (vgl. Abbildung oben)
steht dabei für den Maximalwert (vgl. Abbildung oben)Für Dreieck- und Rechtecksignale siehe Tabelle bei Scheitelfaktor.
Mit einer Pulsweitenmodulation kann der Effektivwert einer Spannung ohne Verlustleistung abgesenkt werden. Es wird während einer festen Periodendauer TPeriode die Spannung nur für einen Teil der Periode Tein eingeschaltet. Der Effektivwert ergibt sich dabei zu:
Beispiele für Effektivwertberechnung
Batterie/Akku
Eine Batterie oder ein Akkumulator liefert eine nahezu konstante elektrische Spannung. Bestimmte Verbraucher entnehmen jedoch oft impulsförmige Ströme. Dadurch kann die Wärmeentwicklung in der Batterie aufgrund ihres Innenwiderstandes sehr viel höher sein, als dieses bei einem Gleichstrom des gleichen arithmetischen Mittelwertes der Fall wäre, da für die Wärmeentwicklung der Effektivwert (quadratischer Mittelwert) des Stromes maßgeblich ist.
Sinusförmige Ströme und Spannungen
Der Wechselstrom der Versorgungsnetze besteht aus einer sinusförmigen Spannungsänderung mit wechselnder Polarität, deren Größe während ihres Ablaufs von Null bis zu einem Maximalwert steigt und dann wieder auf Null zurückgeht. Der Ablauf folgt periodisch den Sinuswerten der Winkel von Null bis 360 Grad und hat daher die Bezeichnung „Sinusform“.
Um die Größenordnung dieser Ströme unabhängig von Momentwerten, Spitzen- und Minimalwerten zu kennzeichnen, wird der Effektivwert angegeben. Beim sinusförmigen Industrie- und Haushalts-Wechselstrom beträgt der Effektivwert
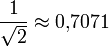 oder 70,71 % des Scheitelwertes der Spannung oder des Stromes.
oder 70,71 % des Scheitelwertes der Spannung oder des Stromes.
(Mathematische Herleitung siehe unten)
Der Scheitelfaktor (Crestfaktor) bezeichnet das Verhältnis zwischen Scheitelwert (Spitzenwert) und Effektivwert. Er ist abhängig von der Wellenform des Signales. Für harmonische (sinusförmige) Signale beträgt er 1,414. Der Scheitelfaktor kann jedoch u. a. bei Gleichrichterschaltungen sehr viel höhere Werte annehmen.
Wird bei der Angabe von Wechselspannung keine zusätzliche Angabe gemacht, so ist immer der Effektivwert gemeint. Im technischen Bereich wird für den Effektivwert häufig der englische Begriff RMS (root mean square) verwendet.
Herleitung: Effektivwert eines Sinussignals
Als Effektivwert eines elektrischen Stromes von wechselnder Größe I(t) wird derjenige Wert angegeben, der in einem (rein ohmschen) Wirkwiderstand R die gleiche Wärmemenge Et erzeugt, wie ein gleich großer Gleichstrom I0 in gleicher Zeit t.
Für den Fall des gleich bleibenden Stromes bei gleich bleibender Spannung gilt:
Damit ergibt sich die Leistung an einem von Gleichstrom durchflossenen ohmschen Widerstand zu:
Die während der Zeit t an diesem Widerstand umgesetzte Energie ergibt sich damit zu:
Es sollen sich jetzt Strom I(t) und Spannung U(t) zeitabhängig ändern. Damit gelten:
Die umgesetzte augenblickliche Leistung berechnet sich analog zu oben zu:
Die augenblickliche Leistung ist immer positiv.
Die während eines Zeitraums t an dem Widerstand umgesetzte Energie ist das Integral über die gesamte zeitabhängige Leistung. Wir wählen den Beginn der Integration willkürlich zu Null:
Jetzt setzen wir die während des Zeitraums t von Gleichstrom und vom zeitabhängigen Strom umgesetzte Energiemenge in das Verhältnis so folgt:
Für die Effektivwerte von Strom und Spannung gilt nach Definition des Effektivwertes:
Damit folgen die bekannten Formeln:
und es erklärt sich der Effektivwert als Wurzel des Mittelwerts der Quadrate...
Im Stromversorgungsnetz
Der in der Leistungsübertragung, und damit in den öffentlichen Versorgungsnetzen, wichtigste Wechselstrom bzw. -spannung ist sinusförmig, mit einer Frequenz von 60 Hertz (USA), 50 Hertz (Europa) und 16⅔ Hertz (Bahn).
Es sollen sich jetzt Strom I(t) und Spannung U(t) sinusförmig ändern. Damit gelten:
Strom und Spannung nehmen innerhalb einer Periode einen Minimal- und einen Maximalwert an, und gehen zweimal durch Null.
Die umgesetzte augenblickliche Leistung berechnet sich analog zu oben zu:
Die augenblickliche Leistung ist bei Verbrauchern immer positiv, sie nimmt während einer Periode von Strom oder Spannung zweimal Minimal- und Maximalwert an.
Die während eines Zeitraums t an dem Widerstand umgesetzte Energie ist das Integral über die gesamte zeitabhängige Leistung. Wir wählen den Beginn der Integration willkürlich zu Null
Jetzt setzen wir die während des Zeitraums t von Gleich- und Wechselstrom umgesetzte Energiemenge in das Verhältnis
Mit
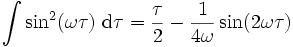 folgt:
folgt:Berücksichtigen wir nur volle Perioden, dass also gilt
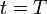 und
und 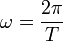 , so folgt:
, so folgt:Ein(e) sinusförmiger Wechselstrom (Wechselspannung) gleicher Amplitude setzt an einem ohmschen Widerstand pro Periode die Hälfte der Energie um wie ein(e) Gleichstrom (Gleichspannung) gleicher Amplitude in der gleichen Zeit. Daraus können wir jetzt den Effektivwert bestimmen.
nach Kürzen ergibt sich:
damit folgt:
Vergleich Effektivwert mit Gleichrichtwert
Der Effektivwert eines Wechselstromes gibt an, welcher Gleichstrom die gleiche Wärmeleistung am Widerstand erbringt wie der Wechselstrom. Der Gleichrichtwert eines Wechselstromes gibt hingegen an, welcher Gleichstrom über die Dauer einer Periode T dieselbe Ladungsmenge transportiert wie ein gleichgerichteter Wechselstrom.
Effektivwert:
Gleichrichtwert:
Ein Vergleich der beiden Größen in Blick auf die Leistung ist nicht möglich, da man die beiden Rechenschritte Quadrieren und Mitteln nicht in der Reihenfolge vertauschen darf.
Das Verhältnis zwischen Effektivwert und Gleichrichtwert bezeichnet man als Formfaktor.
Mit dem Formfaktor lässt sich die Kurvenform einer Wechselgröße beurteilen
Der Formfaktor für sinusförmige Wechselgrößen ist somit:
Messtechnische Erfassung
Falscher und echter Effektivwert
Messgeräte für Wechselspannungen wurden ursprünglich für die Anzeige des Effektivwertes sinusförmiger Spannungen ausgelegt, indem sie den Gleichrichtwert (Mittelwert des Betrages) der Spannung messen und den Formfaktor für Sinus-Spannungen durch entsprechende Justierung der Spannungsteiler einbeziehen; daher ist die Anzeige des Effektivwertes durch solche Messgeräte nur für harmonische (sinusförmige) Spannungen richtig. Da in der Elektrotechnik bzw. Elektronik die Spannungsverläufe häufig stark vom Sinusverlauf abweichen, können hiermit erheblich falsche Messwerte entstehen.
Messgeräte, die den Effektivwert tatsächlich gemäß seiner Definition bestimmen, werden zur Verdeutlichung Echteffektivwert-Messgeräte (engl. true RMS meter) genannt und mit der Bezeichnung True RMS bzw. TRMS ausgewiesen (RMS = root mean square = Wurzel aus dem Mittelwert des Quadrats). Dabei sind sie nur für einen begrenzten Frequenzbereich geeignet.
Elektromechanische Dreheisenmessgeräte arbeiten „TRMS“-bildend und zeigen daher unabhängig vom zeitlichen Verlauf den Effektivwert an. Auch sie sind nur für einen begrenzten Frequenzbereich geeignet.
Eine andere Lösung ist es, mit dem Meßstrom einen Widerstand zu erwärmen und dessen Temperatur zu messen. Durch Vergleich mit einem Gleichstrom kann diese Messanordnung auf den Effektivwert kalibriert werden. Mit dieser Messmethode können auch noch sehr hochfrequente Frequenzanteile richtig erfasst werden.
Effektivwertbildung mit elektrischem Ausgangssignal
Es gibt mehrere elektronische Schaltungen zur Effektivwertbildung. Eine davon hat sich besonders bewährt und wird von mehreren Herstellern als integrierte Schaltung angeboten. Das Eingangssignal Ue oder Ie darf Gleich- und Wechselanteile enthalten. Der Ausgangsstrom Ia ist proportional zum Effektivwert des Eingangssignals, wobei sich die dazu notwendige zeitliche Mittelung aus dem durch R2 und C2 gebildeten Tiefpass ergibt. Die Schaltung arbeitet folgendermaßen (siehe Bild):
In der Eingangsstufe wird ein Strom I1 erzeugt mit
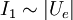 . Der kombinierte Quadrierer und Dividierer erzeugt ein
. Der kombinierte Quadrierer und Dividierer erzeugt ein 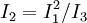 . Dieses Zwischenergebnis wird geglättet und steuert als
. Dieses Zwischenergebnis wird geglättet und steuert als 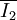 mittels Stromspiegelung zwei Stromquellen. Die eine führt das Signal
mittels Stromspiegelung zwei Stromquellen. Die eine führt das Signal 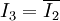 auf den Dividiereingang zurück; die andere liefert das Ausgangssignal
auf den Dividiereingang zurück; die andere liefert das Ausgangssignal 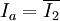 . Damit ergibt sich folgende Rechnung:
. Damit ergibt sich folgende Rechnung:Weblinks
Wikimedia Foundation.

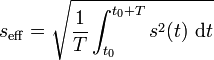
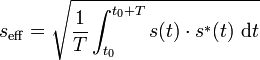
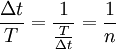
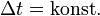
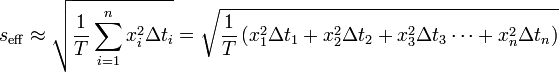
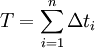
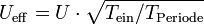

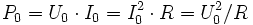
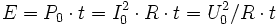
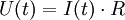
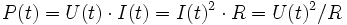
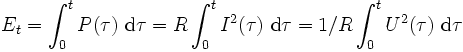
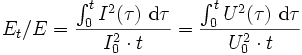
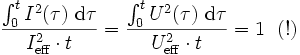
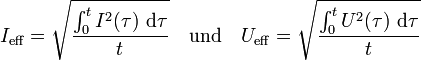
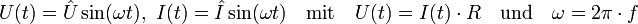
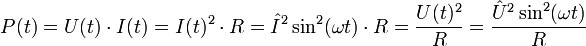
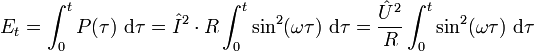
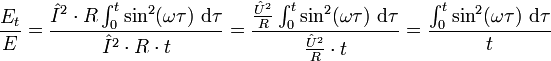
![\frac{E_{t}}{E} = \frac { \left[ \frac {\tau}{2} - \frac {1}{4\omega} \sin(2\omega \tau) \right]_{0}^{t}} {t} \,](/pictures/dewiki/56/88f7dc00a0b73383cf230f9b3bf8f0e2.png)