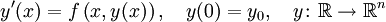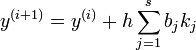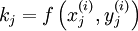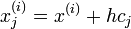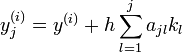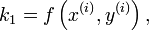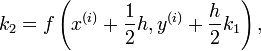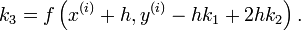Runge-Kutta

Einige Runge-Kutta-Verfahren im Vergleich.

Die s-stufigen Runge-Kutta-Verfahren (nach Carl Runge und Martin Wilhelm Kutta) sind Einschrittverfahren zur näherungsweisen Lösung von Anfangswertproblemen in der numerischen Mathematik. Wenn vom Runge-Kutta-Verfahren gesprochen wird, ist oft das populäre klassische Runge-Kutta-Verfahren gemeint. Dieses bildet jedoch nur einen Spezialfall dieser Familie von Verfahren.

Allgemeine Formulierung

Gegeben sei ein Anfangswertproblem

$y'(x) = f\left(x, y(x)\right), \quad y(0) = y_0, \quad y \colon \R \to \R^n$

mit exakter Lösung y(x). Die exakte Lösung kann im Allgemeinen nicht angegeben werden, weshalb man sich mit einer Näherung y⁽ⁱ⁾ an diskreten Stellen x⁽ⁱ⁾ begnügt. Es gibt verschiedene Methoden zur Berechnung dieser Näherung, z.B. Einschrittverfahren oder Mehrschrittverfahren.

Die s-stufigen Runge-Kutta-Verfahren sind Einschrittverfahren der Art:

$y^{(i+1)} = y^{(i)} + h \sum_{j=1}^s b_j k_j$

h bezeichnet die Schrittweite zwischen den aufeinanderfolgenden Stützstellen x⁽ⁱ⁾ und x⁽ⁱ⁺¹⁾. Die Koeffizienten b_j sind charakteristisch für das jeweilige Verfahren. Die Koeffizienten k_j bezeichnet man als Zwischenschritte. Sie werden bei jedem Berechnungsschritt neu berechnet:

$k_j = f\left(x^{(i)}_j, y^{(i)}_j \right)$

mit

$x^{(i)}_j = x^{(i)} + h c_j$

und

$y^{(i)}_j =y ^{(i)} + h \sum_{l=1}^j a_{jl} k_l$

Die c_j und a_jl sind weitere für das Verfahren charakteristische Koeffizienten. Die Anzahl der Stufen s gibt an, wie viele Funktionsaufrufe pro Schritt benötigt werden.

Im Allgemeinen ist die Rekursionsformel zur Bestimmung der Zwischenschritte implizit. Gilt aber a_jl = 0 für alle 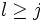$l \ge j$ so ist das Verfahren explizit.

Die Steuerung der Schrittweite h ist auch von besonderem Interesse. Man kann sich leicht vorstellen, dass die Funktion in Bereichen, in denen nur geringe Änderungen zwischen y^{(i + 1)} und y⁽ⁱ⁾ vorliegen, mit weniger Rechenschritten auskommt, als in solchen, wo schnelle Änderungen vorliegen.

Beispiel

Ein Beispiel ist das dreistufige Runge-Kutta-Verfahren: 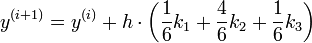$y^{(i+1)} = y^{(i)} + h \cdot \bigg( \frac{1}{6}k_1 + \frac{4}{6}k_2 + \frac{1}{6}k_3 \bigg)$ mit den Zwischenstufen

$k_1 = f\left(x^{(i)}, y^{(i)}\right),$

$k_2 = f\left(x^{(i)}+\frac{1}{2}h, y^{(i)}+\frac{h}{2}k_1\right),$

$k_3 = f\left(x^{(i)}+h, y^{(i)}-h k_1+2h k_2\right).$

Runge-Kutta-Tableau

Man kann die charakteristischen Koeffizienten c_j, b_j, a_jl übersichtlich im sogenannten Runge-Kutta-Tableau (auch Butcher-Schema, -Tableau oder engl. Butcher array genannt) anordnen. Hierbei ist die Matrix A bei einem expliziten Verfahren eine strikte untere Dreiecksmatrix.

$\begin{array}{c|c} \mathbf{c} & A\\ \hline & \mathbf{b^T} \\ \end{array} = \begin{array}{c|cccc} c_1 & a_{11} & a_{12}& \dots & a_{1s}\\ c_2 & a_{21} & a_{22}& \dots & a_{2s}\\ \vdots & \vdots & \vdots& \ddots& \vdots\\ c_s & a_{s1} & a_{s2}& \dots & a_{ss}\\ \hline & b_1 & b_2 & \dots & b_s\\ \end{array}\; , \qquad c = \begin{bmatrix} c_1 \\ \vdots \\ c_j \\ \vdots \\ c_s \end{bmatrix} \;, \quad b = \begin{bmatrix} b_1 \\ \vdots \\ b_j \\ \vdots \\ b_s \end{bmatrix} \;, \quad A = \begin{bmatrix} a_{11} & \dots & a_{1l} & \dots & a_{1s}\\ \vdots & \ddots & \vdots & \ddots & \vdots\\ a_{j1} & \dots & a_{jl} & \dots & a_{js}\\ \vdots & \ddots & \vdots & \ddots & \vdots\\ a_{s1} & \dots & a_{sl} & \dots & a_{ss}\\ \end{bmatrix} \;.$

Konsistenzordnung und Konvergenzordnung

Eine wichtige Eigenschaft zum Vergleich von Verfahren ist die Konsistenzordnung, die auf dem Begriff des lokalen Diskretisierungsfehlers τ beruht. Ein Einschrittverfahren heißt konsistent von der Ordnung p (hat Konsistenzordnung p), falls gilt: 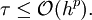$\tau \le \mathcal{O}(h^p).$ (Zur Notation, siehe Landau-Symbole)

Je nach Definition des Diskretisierungsfehlers kann allerdings auch 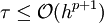$\tau \le \mathcal{O}(h^{p+1})$ gefordert sein. Beide Definitionen sind sinnvoll und haben in verschiedenen Bereichen ihre Vorteile.

Ist 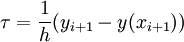$\tau=\frac{1}{h}(y_{i+1}-y(x_{i+1}))$ definiert, so muss 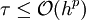$\tau \le \mathcal{O}(h^p)$ gelten. Wird hingegen τ = y_{i + 1} − y(x_{i + 1}) definiert, so muss 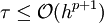$\tau \le \mathcal{O}(h^{p+1})$ gelten.

Dabei ist y_{i + 1} die numerische Lösung nach einem Schritt und y(x_{i + 1}) die exakte Lösung. Die Konsistenzordnung kann durch Taylorentwicklung von τ, oder durch Taylorentwicklung der exakten und numerischen Lösung bestimmt werden. Allgemein gilt:

Konsistenzordnung p und Stabilität $\Rightarrow$ Konvergenzordnung p

Bei Einschrittverfahren, wie den Runge-Kutta-Verfahren gilt sogar, sofern f und die Verfahrensvorschrift Lipschitz-stetig sind:

Konsistenzordnung p $\Rightarrow$ Konvergenzordnung p

Aus der Konsistenzbedingung (z.B. das Verfahren soll Ordnung 4 haben) ergeben sich Konsistenzgleichungen (engl. conditions) für die Koeffizienten des Runge-Kutta-Verfahrens. Die Gleichungen und ihre Anzahl können mit Hilfe von Taylorentwicklung oder der Theorie der Butcher-Bäume ermittelt werden. Mit zunehmender Ordnung wächst die Zahl der zu lösenden nicht-linearen Konsistenzgleichungen schnell an. Das Aufstellen der Konsistenzgleichungen ist bereits nicht einfach; kann jedoch mit Hilfe der Butcher-Bäume von Computeralgebrasystemen erledigt werden. Das Lösen ist allerdings noch schwieriger und bedarf Erfahrung und Fingerspitzengefühl, um „gute“ Koeffizienten zu erhalten.

Im allgemeinen kann ein explizites s-stufiges Runge-Kutta-Verfahren höchstens Konvergenzordnung s haben, dagegen ein implizites idealerweise Konvergenzordnung 2s.

Explizite Verfahren haben den Vorteil, dass die zu lösenden Gleichungssysteme wesentlich einfacher sind, da sie immer durch sukzessives Einsetzen lösbar sind. Daher kommen Implizite Runge-Kutta-Verfahren meist nur bei steifen Differentialgleichungen oder Differentiell-algebraischen Gleichungen zum Einsatz.

Um die Genauigkeit eines Ergebnisses zu verbessern gibt es im Grunde zwei Möglichkeiten.

1. Man kann die Schrittweite verkleinern, das heißt man erhöht die Anzahl der Diskretisierungspunkte.
2. Man kann Verfahren höherer Konvergenzordnung wählen

Welche Strategie die bessere ist, hängt von der konkreten Problemstellung ab, die Erhöhung der Konvergenzordnung ist allerdings nur bis zu einer bestimmten Grenze sinnvoll, da

1. die Anzahl der zu lösenden Bestimmungsgleichungen exponentiell mit der Ordnung des Verfahrens wächst.
2. Wegen der Butcher-Schranken die Stufenzahl s schneller wächst als die Ordnung p.

Beispiele

Das explizite Euler-Verfahren (Ordnung 1):

$\begin{array}{c|c} 0 \\ \hline & 1 \end{array}$

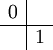
Das Heun-Verfahren (Ordnung 2):

$\begin{array}{c|cc} 0 \\ 1 & 1 \\ \hline & \frac{1}{2} & \frac{1}{2} \end{array}$

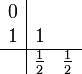
Das Runge-Kutta-Verfahren der Ordnung 2:

$\begin{array}{c|cc} 0 \\ \frac{1}{2} & \frac{1}{2} \\ \hline & 0 & 1 \end{array}$

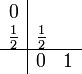
Das Runge-Kutta-Verfahren der Ordnung 3 (vgl. Simpsonregel):

$\begin{array}{c|ccc} 0 \\ \frac{1}{2} & \frac{1}{2} \\ 1 & -1 & 2 \\ \hline & \frac{1}{6} & \frac{4}{6} & \frac{1}{6} \end{array}$

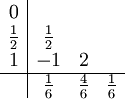
Das Heun-Verfahren 3. Ordnung:

$\begin{array}{c|ccc} 0 \\ \frac{1}{3} & \frac{1}{3} \\ \frac{2}{3} & 0 & \frac{2}{3} \\ \hline & \frac{1}{4} & 0 & \frac{3}{4} \end{array}$

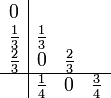
Das klassische Runge-Kutta-Verfahren (Ordnung 4):

$\begin{array}{c|cccc} 0 \\ \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & 0 & \frac{1}{2} \\ 1 & 0 & 0 & 1 \\ \hline & \frac{1}{6} & \frac{1}{3} & \frac{1}{3} & \frac{1}{6} \end{array}$

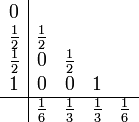
Das implizite Trapez-Verfahren der Ordnung 2:

$\begin{array}{c|cc} 0 \\ 1 & \frac{1}{2} & \frac{1}{2} \\ \hline & \frac{1}{2} & \frac{1}{2} \end{array}$

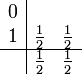
Literatur

• J. C. Butcher: The Numerical Analysis of Ordinary Differential Equations: Runge-Kutta and General Linear Methods, 1987.
• E. Fehlberg: Klassische Runge-Kutta Formeln 5. und 7. Ordnung mit Schrittweitenkontrolle. Computing, 4(2), 93-106, 1969.
• Lambert Numerical Methods for Ordinary Differential Systems, The Initial Value Problem, 1991.
• Sofroniou Symbolic Derivation of Runge-Kutta Methods, 1994.
• M. Hermann: Numerik gewöhnlicher Differentialgleichungen, Anfangs- und Randwertprobleme. München und Wien: Oldenbourg, 2004. ISBN 3-486-27606-9
• Folkmar Bornemann Runge-Kutta Methods, Trees, and Maple Selçuk J. Appl. Math. 2, pp. 3-15 (2001). Version using Mathematica: E-print arXiv:math.NA/0211049
• Peter Deuflhard, Folkmar Bornemann: Numerische Mathematik 2. ISBN 3-11-017181-3
• Ernst Hairer, Gerhard Wanner: Solving Ordinary Differential Equations 1. Nonstiff Problems ISBN 3-540-56670-8
• P. Albrecht: The Runge-Kutta Theory in a Nutshell, SIAM J. Numer. Anal.33, 1712 - 1735, 1996.