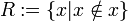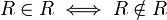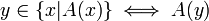Russell Paradox

Die Russellsche Antinomie ist ein von Bertrand Russell und Ernst Zermelo entdecktes Paradoxon der Naiven Mengenlehre, das Russell 1903 publizierte und daher seinen Namen trägt.

Begriff und Problematik

Russell bildete seine Antinomie mit Hilfe der „Klasse aller Klassen, die sich nicht selbst als Element enthalten“.^[1] Sie wird als Russellsche Klasse bezeichnet und formal folgendermaßen definiert:

$R :=\{x|x\notin x\}$

Oft wird die Russellsche Klasse auch als „Menge aller Mengen, die sich nicht selbst als Element enthalten“ definiert; das entspricht der damaligen Mengenlehre, die noch nicht zwischen Klassen und Mengen unterschied. Die Russellsche Antinomie ist aber im Gegensatz zu den älteren Antinomien der naiven Mengenlehre (Burali-Forti-Paradoxon und Cantorschen Antinomie) rein logischer Natur und unabhängig von Mengenaxiomen. Daher hat sie besonders stark gewirkt und schlagartig das Ende der naiven Mengenlehre herbeigeführt.

Russell leitete seine Antinomie sinngemäß so ab:^[2] Angenommen 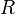$\,R$ enthält sich selbst, dann gilt aufgrund der Klasseneigenschaft, mit der 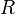$\,R$ definiert wurde, dass 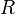$\,R$ sich nicht enthält, was der Annahme widerspricht. Angenommen es gilt das Gegenteil und 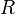$\,R$ enthält sich nicht selbst, dann erfüllt 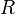$\,R$ die Klasseneigenschaft, so dass 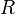$\,R$ sich doch selbst enthält entgegen der Annahme. Mathematisch drückt dies folgende widersprüchliche Äquivalenz aus:

$R \in R \iff R \notin R$

Zur Ableitung dieses Widerspruchs werden keine Axiome und Sätze der Mengenlehre benutzt, sondern außer der Definition nur Freges Abstraktionsprinzip:^[3]

$y \in \{x|A(x)\} \iff A(y)$

Geschichte und Lösungen

Es ist nicht bekannt, wann genau Russell sein Paradoxon entdeckte, vermutlich im Frühjahr 1901 bei der Arbeit an seinem Buch The Principles of Mathematics, in dem er 1903 die Antinomie publizierte. Schon 1902 teilte er die Antinomie Gottlob Frege brieflich mit.^[4] Er bezog sich auf Freges ersten Band der Grundgesetze der Arithmetik von 1893, in der Frege die Arithmetik auf ein mengentheoretisches Axiomensystem aufzubauen versuchte. Die Russellsche Antinomie zeigte, dass dieses Axiomensystem widersprüchlich war. Frege reagierte darauf im Nachwort des zweiten Bands seiner Grundgesetze der Arithmetik von 1903:

Einem wissenschaftlichen Schriftsteller kann kaum etwas Unerwünschteres begegnen, als daß ihm nach Vollendung einer Arbeit eine der Grundlagen seines Baues erschüttert wird. In diese Lage wurde ich durch einen Brief des Herrn Bertrand Russell versetzt, als der Druck dieses Bandes sich seinem Ende näherte.^[5]

Vermutlich gab Frege seine Arbeiten auf dem Gebiet der axiomatischen Logik aufgrund der Entdeckung des Paradoxons auf.

Russell löste das Paradoxon bereits 1903 durch seine Typentheorie; in ihr hat eine Klasse stets einen höheren Typ als ihre Elemente; Aussagen wie „eine Klasse enthält sich selbst“, mit der er seine Antinomie bildete, lassen sich dann gar nicht mehr formulieren.^[6] Er versuchte also, da er an Freges Abstraktionsprinzip festhielt^[7], das Problem durch eine eingeschränkte Syntax der zulässigen Klassen-Aussagen zu lösen. Die eingeschränkte Syntax erwies sich aber als kompliziert und unzulänglich zum Aufbau der Mathematik und hat sich nicht dauerhaft durchgesetzt.

Parallel zu Russell entwickelte Zermelo, der die Antinomie unabhängig von Russell fand und schon vor Russells Publikation kannte,^[8] die erste axiomatische Mengenlehre mit uneingeschränkter Syntax. Das Aussonderungsaxiom dieser Zermelo-Mengenlehre von 1907 gestattet nur noch eine eingeschränkte Klassenbildung innerhalb einer gegebenen Menge. Er zeigte durch einen indirekten Beweis mit dieser Antinomie, dass die Russellsche Klasse keine Menge ist.^[9] Sein Lösungsweg hat sich durchgesetzt. In der erweiterten Zermelo-Fraenkel-Mengenlehre (ZF), die heute als Grundlage der Mathematik dient, stellt zusätzlich das Fundierungsaxiom sicher, dass keine Menge sich selbst enthalten kann, so dass hier die Russellsche Klasse identisch mit der Allklasse ist.

Da die Russellsche Antinomie rein logischer Natur ist und nicht von Mengenaxiomen abhängt, ist schon auf der Ebene der widerspruchsfreien Prädikatenlogik erster Stufe beweisbar, dass die Russellsche Klasse als Menge nicht existent ist. Das macht folgende Argumentation einsichtig, die einen zweiten indirekten Beweis Russells^[10] aufgreift und in einen direkten Beweis umwandelt:

Aussagenlogisch gilt offenbar die Aussage 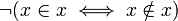$\neg (x\in x\iff x\notin x)$ für beliebige $\,x$.

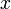Daher kann der Existenzquantor eingeführt werden und es gilt $\exists y \colon \neg (y\in x\iff y\notin y)$.

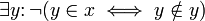Durch Einführung des Allquantors ergibt sich $\forall x \colon \exists y \colon \neg (y\in x\iff y\notin y)$.

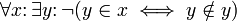Durch Umformung der Quantoren erhält man dann $\neg \exists x \colon \forall y \colon (y\in x\iff y\notin y)$.

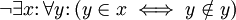Dieser Satz bedeutet in der prädikatenlogischen Sprache genau: Es gibt keine Menge aller Mengen, die sich selbst nicht als Element enthalten.

Der Satz gilt in allen modernen axiomatischen Mengenlehren, die auf der Prädikatenlogik erster Stufe aufbauen, zum Beispiel in ZF. Er gilt auch in der Neumann-Bernays-Gödel-Mengenlehre, in der aber die Russellsche Klasse als echte Klasse existiert. In der Klassenlogik von Oberschelp, die eine nachweislich widerspruchsfreie Erweiterung der Prädikatenlogik erster Stufe ist, können zudem beliebige Klassenterme zu beliebigen definierenden Aussagen gebildet werden; speziell ist dort auch die Russellsche Klasse ein korrekter Term mit beweisbarer Nichtexistenz.^[11] In diese Klassenlogik können Axiomensysteme wie die ZF-Mengenlehre eingebunden werden.

Varianten der Russellschen Antinomie

Die Grelling-Nelson-Antinomie von 1908 ist ein durch die Russellsche Antionomie inspiriertes semantisches Paradoxon.

Es gibt zahlreiche populäre Varianten der Russellschen Antinomie. Am bekanntesten ist das von Russell 1918 formulierte Barbier-Paradoxon mit einem Barbier, der genau die Männer rasiert, die sich nicht selbst rasieren. Die Frage, ob sich der Barbier selbst rasiert oder nicht, führt ebenfalls zu einem Widerspruch, der allerdings nicht dieselbe logische Brisanz hat.

Einzelnachweise

1. ↑ Bertrand Russell: The principles of Mathematics, Cambridge 1903, Kap. X, Zusammenfassung §106.
2. ↑ Bertrand Russell: The principles of Mathematics, Cambridge 1903, §101.
3. ↑ Gottlob Frege: Grundgesetze der Arithmetik, I, 1893, S. 52.
4. ↑ Russells Brief an Frege vom 16. Juni 1902. In: Gottlob Frege: Briefwechsel mit D.Hilbert, E. Husserl, B. Russell, ed. G. Gabriel, F. Kambartel, C.Thiel, Hamburg 1980, S. 59f.
5. ↑ Gottlob Frege: Grundlagen der Arithmetik, II, 1903, Anhang S. 253-261.
6. ↑ Bertrand Russell: The principles of Mathematics, Cambridge 1903, §§497-500.
7. ↑ Russell/Whitehead: Principia mathematica I, Cambridge 1910, S. 26
8. ↑ laut einem Brief von Hilbert vom 7.11.1903, in: Gottlob Frege: Briefwechsel mit D.Hilbert, E. Husserl, B. Russell, ed. G. Gabriel, F. Kambartel, C.Thiel, Hamburg 1980, S. 23f/47.
9. ↑ Ernst Zermelo: Untersuchungen über die Grundlagen der Mengenlehre, Mathematische Annalen 65 (1908), S. 261-281; dort S. 265.
10. ↑ Bertrand Russell: The principles of mathematics, Cambridge 1903, §102. Dort ist die Ableitung für eine beliebige Relation R und speziell für 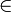$\in$ formuliert.
11. ↑ Arnold Oberschelp: Allgemeine Mengenlehre, Mannheim, Leipzig, Wien, Zürich, 1994, S. 37.

Weblinks

• A. D. Irvine: Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und Parameter 3 und nicht Parameter 2
• Kevin C. Klement: Eintrag in der Internet Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)