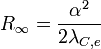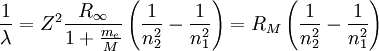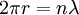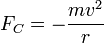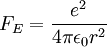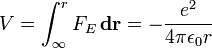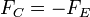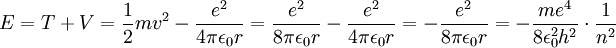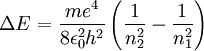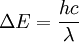- Rydbergkonstante
-
Die Rydberg-Konstante R∞ ist eine nach Johannes Rydberg benannte Naturkonstante, die bei der Berechnung der Spektrallinien von Atomen eine bedeutende Rolle spielt.
Ihr derzeit allgemein empfohlener Wert beträgt nach CODATA 2006[1][2]
- R∞ = 10 973 731,568 527 (73) m-1
Sie kann demnach auf eine relative Standardabweichung von 6,6 × 10-12 genau angegeben werden und ist damit die am genauesten messbare Naturkonstante überhaupt. Sie ergibt sich aus der Feinstrukturkonstante α und der Compton-Wellenlänge eines Elektrons, λC,e nach
Die Wellenlängen der Spektrallinien von wasserstoffähnlichen Atomen (also Ionen mit einem einzigen Elektron) können anhand der Formel
bestimmt werden. Dabei ist Z die Anzahl der Protonen im Kern (für Wasserstoff ist Z=1), M die Masse des Kerns und λ die Wellenlänge des vom Elektron emittierten Photons. Weiter bezeichnet n1 die Quantenzahl des Orbits, von dem aus das Elektron in den tiefer gelegenen Orbit n2 übergeht - also etwa vom dritten Orbit n1=3 in den zweiten n2=2.
Den Einfluss der Kernladung Z und der Kernmasse M (abhängig auch vom vorliegenden Isotop des Elements) berücksichtigt man in
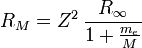 .
.
Häufig werden auch Rydberg-Frequenz R und die Rydberg-Energie Ry als Rydberg-Konstante angegeben. Diese betragen
- Rydberg-Frequenz:
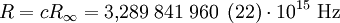
- Rydberg-Energie:
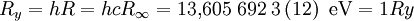
Letzteres ist gerade die Ionisierungsenergie des Wasserstoffs und wird ein Rydberg der Energie genannt.
Herleitung
Die Rydberg-Konstante lässt sich über die bohrsche Bedingung, die Zentrifugalkraft, die Coulombkraft, und die elektrische potenzielle Energie eines Elektrons im Orbit um ein Proton berechnen.
- Die bohrsche Bedingung ist
wobei r der Radius des Elektronenorbits bezeichnet.
- Für die Zentrifugalkraft gilt
- Coulombkraft zwischen Proton und Elektron
- Die potenzielle Energie im Abstand r zum Proton beträgt
Mit der Beziehung von de Broglie
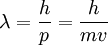 erhalten wir aus der Bohrschen Bedingung
erhalten wir aus der Bohrschen Bedingung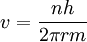 (1)
(1)
Für eine stabile Bahn gilt klassisch
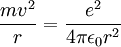 (2)
(2)
Nach Einsetzen von (1) in diese Beziehung ergibt sich für den Radius
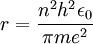 (3)
(3)
Unter den gemachten Annahmen sind dies also die einzigen erlaubten Radien für ein sich um ein Proton bewegendes Elektron.
Außerdem folgt aus (2) für die Geschwindigkeit
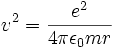 (4)
(4)
Aus (3) und (4) ergibt sich für die Gesamtenergie
Jeder Orbit besitzt demnach eine bestimmte potenzielle und kinetische Energie, sodass bei einer Änderung des Orbits von n1 nach n2 auch eine Energieänderung stattfindet. Diese Änderung ist gerade
Oder mit
als Wellenlängenänderung geschrieben
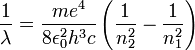 .
.
Da hier ein e2 die Ladung des Kerns repräsentiert, muss für allgemeine Atome die Kernladungszahl Z hinzugefügt werden. Damit gilt
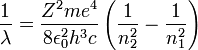 .
.
Die Rydberg-Konstante von Wasserstoff ist daher gerade
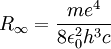 .
.
Dieses Ergebnis wurde erstmals von Niels Bohr als Folgerung seines Atommodells bestimmt.
Für den genauen Wert von R bzw. der Energieniveaus des Wasserstoffs muss die Mitbewegung des Kerns berücksichtigt werden, weshalb die Elektronenmasse durch die reduzierte Masse µ ersetzt wird.
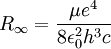 , mit
, mit 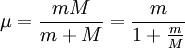
Quellen
- ↑ CODATA Internationally recommended values of the Fundamental Physical Constants 2006
- ↑ http://physics.nist.gov/cgi-bin/cuu/Value?ryd
Siehe auch
Wikimedia Foundation.