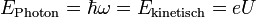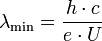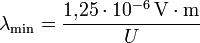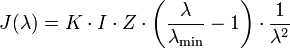Röntgenkontinuum

Erzeugung von Röntgenbremsstrahlung durch Abbremsung eines schnellen Elektrons in dem Coulombfeld eines Atomkerns (schematische Darstellung)

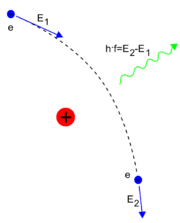
Bremsstrahlung ist die elektromagnetische Strahlung, die entsteht, wenn ein geladenes Teilchen, zum Beispiel ein Elektron, beschleunigt wird. Jede Geschwindigkeitsänderung eines geladenen Teilchens erzeugt Strahlung. Von Bremsstrahlung im engeren Sinne spricht man, wenn Teilchen in Materie gebremst werden.

Auftreten bzw. Anwendung der Bremsstrahlung

Bei Teilchenbeschleunigern (vor allem beim Synchrotron) und bei Speicherringen wird bei der Ablenkung von geladenen Teilchen durch ein Magnetfeld Bremsstrahlung frei, die in diesen Zusammenhängen Synchrotronstrahlung genannt wird.

Der Effekt der Bremsstrahlung wird in Röntgenröhren zur Erzeugung von Röntgenstrahlung verwendet. Dabei schießt man in Elektronen mit einer kinetischen Energie von einigen 10 bis 100 keV auf eine Metallplatte, die häufig aus Wolfram besteht. Ein kleiner Teil der beim Abbremsen frei werdenden Energie wird in Röntgenstrahlung mit einem kontinuierlichen Spektrum umgewandelt.

Spektralverteilung der Bremsstrahlung bei einer Röntgenröhre

Das Spektrum hat zu kurzen Wellenlängen hin eine der kinetischen Energie der Elektronen entsprechende Grenzwellenlänge, d. h. die gesamte kinetische Energie der Elektronen wird in Röntgenstrahlung umgewandelt. Diese Grenzwellenlänge hängt also nur von der durchlaufenen Beschleunigungsspannung (Anodenspannung) ab, sie ist unabhängig vom Anodenmaterial. Die Form des Spektrums hängt von der Geschwindigkeitsverteilung der Elektronen und dem verwendeten Metall ab.

Die minimale Wellenlänge tritt auf, wenn die gesamte kinetische Energie des Elektrons in ein einziges Photon umgewandelt wird:

$E_\text{Photon} = \hbar\omega = E_\text{kinetisch} = eU$

Sie beträgt

${\lambda_\mathrm{min}} = \frac{h \cdot c}{e \cdot U}$

mit

c - Lichtgeschwindigkeit

h - Plancksches Wirkungsquantum

e - Elementarladung, Elektronenladung

U - Beschleunigungsspannung, Anodenspannung der Röntgenröhre

Durch Einsetzen der Naturkonstanten ergibt sich die zugeschnittene Größengleichung

${\lambda_\mathrm{min}} = \frac{1{,}25\cdot 10^{-6}\,\mathrm{V}\cdot \mathrm{m}}{U}$  ^[1]

Auch aus dieser Gleichung sieht man, dass die untere Grenzwellenlänge λ_min nur von der Beschleunigungsspannung U abhängig ist. Bei einer Beschleunigungsspannung von 25 Kilovolt beträgt sie zum Beispiel 0,05 nm. Diese Strahlung vermag bereits dünnes Glas und Aluminium zu durchdringen. Daher muss man zum Beispiel bei Bildröhren, die etwa mit dieser Spannung arbeiten, Maßnahmen zum Strahlenschutz treffen. Man verwendet daher zum Beispiel Bleioxid-haltiges Kolbenglas.

Die kontinuierliche Intensitätsverteilung der Bremsstrahlung, wenn Elektronen in ein Material eintreten, folgt der Kramerschen Regel^[2]:

$J({\lambda}) = K \cdot I \cdot Z \cdot \left(\frac{\lambda}{\lambda_\mathrm{min}}-1\right) \cdot \frac{1}{\lambda^2}$

mit

J - Intensitätsfunktion, in Photonen pro Sekunde

K - die so genannte Kramersche Konstante

I - Elektronenstrom

Z - Ordnungszahl der Atome des Materials

Bei realen Spektren von Röntgenemissionen wird die entstehende Bremsstrahlung durch verschiedene Effekte überlagert. Hinzu kommt insbesondere die charakteristische Strahlung, die ein Emissionsspektrum der Atome des Materials darstellt, sowie dessen Absorptionsbanden, da die Bremsstrahlung unter der Materialoberfläche entsteht.

Anwendung

Die Messung der Grenzwellenlänge λ_min ist eine Möglichkeit zur Präzisionsbestimmung des planckschen Wirkungsquantums h.

Einzelnachweise

1. ↑ http://www.pctheory.uni-ulm.de/didactics/quantenchemie/html/Roentgen.html Röntgenbremsstrahlung / Universität Ulm
2. ↑ http://www.immr.tu-clausthal.de/geoch/labs/XRF/RFA/Kapitel1.html

Weblinks

• http://www.desy.de/pr-info/Roentgen-light/roentgenstrahlung/roentgenstrahlung8.html
• Spektrum der Röntgenbremsstrahlung