- S-Raum
-
Unter einem Schwartz-Raum versteht man in der Mathematik eine spezielle Klasse lokalkonvexer Vektorräume. Viele in den Anwendungen wichtige Räume, z. B. Räume differenzierbarer Funktionen, sind Schwartz-Räume. Der Raum
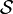 der schnell fallenden Funktionen (s.u.) wird in der Distributionstheorie manchmal als der Schwartz-Raum bezeichnet, obwohl es sich lediglich um einen Vertreter der hier zu besprechenden Raumklasse handelt. Die Bezeichnung Schwartz-Raum (nach Laurent Schwartz) geht auf Alexander Grothendieck zurück. In der Literatur ist auch die Bezeichnung S-Raum verbreitet; ein vollständiger Schwartz-Raum wird dann auch ein
der schnell fallenden Funktionen (s.u.) wird in der Distributionstheorie manchmal als der Schwartz-Raum bezeichnet, obwohl es sich lediglich um einen Vertreter der hier zu besprechenden Raumklasse handelt. Die Bezeichnung Schwartz-Raum (nach Laurent Schwartz) geht auf Alexander Grothendieck zurück. In der Literatur ist auch die Bezeichnung S-Raum verbreitet; ein vollständiger Schwartz-Raum wird dann auch ein  -Raum genannt.
-Raum genannt.Inhaltsverzeichnis
Definition
Ein lokalkonvexer Raum E heißt ein Schwartz-Raum, wenn es zu jedem normierten Raum F und jedem stetigen linearen Operator
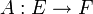 eine Nullumgebung
eine Nullumgebung 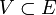 gibt, so dass das Bild A(V) präkompakt ist.
gibt, so dass das Bild A(V) präkompakt ist.Dies ist genau dann der Fall, wenn es zu jedem Banachraum F und jedem stetigen linearen Operator
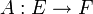 eine Nullumgebung
eine Nullumgebung 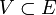 gibt, so dass
gibt, so dass 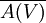 kompakt ist.
kompakt ist.Eine innere Charakterisierung lautet:
Ein lokalkonvexer Raum E ist genau dann ein Schwartz-Raum, wenn es zu jeder Nullumgebung
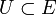 eine Nullumgebung
eine Nullumgebung 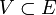 gibt, so dass man zu jedem ε > 0 endlich viele Punkte
gibt, so dass man zu jedem ε > 0 endlich viele Punkte  mit
mit  finden kann.
finden kann.Präkompakte Halbnormen
Weiter lassen sich Schwartz-Räume über die stetigen Halbnormen charakterisieren. Eine Halbnorm p auf einem lokalkonvexen Raum E heißt präkompakt, falls es eine Nullfolge (ζn)n in
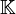 und eine gleichstetige Folge (fn)n im starken Dualraum
und eine gleichstetige Folge (fn)n im starken Dualraum 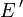 gibt, so dass für alle
gibt, so dass für alle 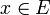 die Ungleichung
die Ungleichung  gilt. (Dabei heißt die Folge (fn)n gleichstetig, wenn es eine stetige Halbnorm q auf E gibt mit
gilt. (Dabei heißt die Folge (fn)n gleichstetig, wenn es eine stetige Halbnorm q auf E gibt mit  für alle
für alle 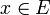 und
und 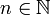 .)
.)Präkompakte Halbnormen sind stetig, denn mit obigen Bezeichnungen erhält man die Abschätzung
 . Die Umkehrung ist im Allgemeinen nicht richtig, sie stellt vielmehr eine Charakterisierung der Schwartz-Räume dar, denn es gilt:
. Die Umkehrung ist im Allgemeinen nicht richtig, sie stellt vielmehr eine Charakterisierung der Schwartz-Räume dar, denn es gilt:Ein lokalkonvexer Raum E ist genau dann ein Schwartz-Raum, wenn jede stetige Halbnorm präkompakt ist.
Beispiele
- Unter den normierten Räumen sind genau die endlich-dimensionalen Räume Schwartz-Räume.
- Jeder vollständige nukleare Raum ist ein Schwartz-Raum.
- Sei
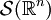 der Raum aller Funktionen
der Raum aller Funktionen 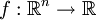 , für die alle Suprema
, für die alle Suprema 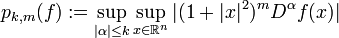 endlich sind. Dabei wurde von der Multiindex-Schreibweise Gebrauch gemacht. Der Raum
endlich sind. Dabei wurde von der Multiindex-Schreibweise Gebrauch gemacht. Der Raum 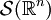 mit den Halbnormen
mit den Halbnormen 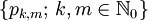 heißt Raum der schnell fallenden Funktionen. Er ist ein Schwartz-Raum und wird manchmal auch als der Schwartz-Raum bezeichnet.
heißt Raum der schnell fallenden Funktionen. Er ist ein Schwartz-Raum und wird manchmal auch als der Schwartz-Raum bezeichnet. - Jede Folge
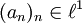 definiert durch die Festlegung
definiert durch die Festlegung  ein lineares Funktional auf dem Folgenraum
ein lineares Funktional auf dem Folgenraum 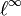 der beschränkten Folgen. Diesen Raum versehe man mit der feinsten lokalkonvexen Topologie, so dass der Dualraum bzgl. dieser Identifikation mit
der beschränkten Folgen. Diesen Raum versehe man mit der feinsten lokalkonvexen Topologie, so dass der Dualraum bzgl. dieser Identifikation mit 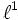 zusammenfällt. Nach dem Satz von Mackey-Arens gibt es eine solche Topologie, die Mackey-Topologie
zusammenfällt. Nach dem Satz von Mackey-Arens gibt es eine solche Topologie, die Mackey-Topologie  . Der lokalkonvexe Raum
. Der lokalkonvexe Raum 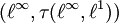 ist ein vollständiger Schwartz-Raum, der nicht nuklear ist.
ist ein vollständiger Schwartz-Raum, der nicht nuklear ist.
Eigenschaften
- Unterräume und Quotientenräume nach abgeschlossenen Unterräumen von Schwartz-Räumen sind wieder Schwartz-Räume.
- Beliebige Produkte von Schwartz-Räumen sind wieder Schwartz-Räume.
- Vollständige quasitonnelierte Schwartz-Räume sind Montel-Räume. Es gibt aber Fréchet-Montel-Räume, die keine Schwartz-Räume sind.
- Ein lokalkonvexer Raum E ist genau dann ein Schwartz-Raum, wenn es eine Menge I gibt, so dass E topologisch isomorph zu einem Unterraum von
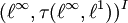 ist. In diesem Sinne ist
ist. In diesem Sinne ist 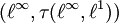 ein universeller Schwartz-Raum.
ein universeller Schwartz-Raum.
Vollständige Schwartz-Räume
Vollständige Schwartz-Räume haben besondere Eigenschaften und lassen weitere Charakterisierungen zu. Ist p eine stetige Halbnorm auf dem lokalkonvexen Raum E, so ist
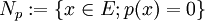 ein abgeschlossener Unterraum von E und durch
ein abgeschlossener Unterraum von E und durch 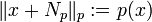 wird eine Norm auf dem Faktorraum Ep: = E / Np erklärt. Die Vervollständigung dieses normierten Raums wird mit Bp bezeichnet. Ist q eine weitere stetige Halbnorm mit
wird eine Norm auf dem Faktorraum Ep: = E / Np erklärt. Die Vervollständigung dieses normierten Raums wird mit Bp bezeichnet. Ist q eine weitere stetige Halbnorm mit 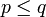 , so definiert
, so definiert 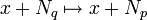 einen stetigen linearen Operator
einen stetigen linearen Operator 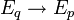 , der sich stetig zu einem linearen Operator
, der sich stetig zu einem linearen Operator 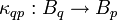 fortsetzen lässt. Die Bp heißen die lokalen Banachräume und die Operatoren κqp heißen kanonische Abbildungen von E. Mit diesen Begriffen können vollständige Schwartz-Räume wie folgt charakterisiert werden:
fortsetzen lässt. Die Bp heißen die lokalen Banachräume und die Operatoren κqp heißen kanonische Abbildungen von E. Mit diesen Begriffen können vollständige Schwartz-Räume wie folgt charakterisiert werden:Ein lokalkonvexer Raum ist genau dann ein vollständiger Schwartz-Raum, wenn es zu jeder stetigen Halbnorm p eine weitere stetige Halbnorm
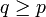 gibt, so dass die kanonische Abbildung
gibt, so dass die kanonische Abbildung 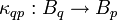 ein kompakter Operator ist.
ein kompakter Operator ist.Es genügt natürlich, sich auf ein gerichtetes System erzeugender Halbnormen zu beschränken.
In vollständigen Schwartz-Räumen gilt der Satz von Bolzano-Weierstraß, das heißt, eine Menge ist genau dann kompakt, wenn sie abgeschlossen und beschränkt ist.
Literatur
- K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume. Lecture Notes in Mathematics 56, 1968.
- H. H. Schaefer: Topological Vector Spaces. Springer, 1971.
- H. Jarchow: Locally Convex Spaces. Teubner, Stuttgart 1981.
- Yau-Chuen Wong: Introductory Theory of Topological Vector Spaces. Marcel Dekker Ltd., 1992.
- R. Meise, D. Vogt: Einführung in die Funktionalanalysis. Vieweg, 1992. ISBN 3-528-07262-8
Wikimedia Foundation.
