SO(3,R)

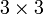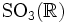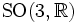Die Drehgruppe ist in der mathematischen Gruppentheorie die Gruppe, deren Elemente den Drehungen eines dreidimensionalen reellen Raumes entsprechen. Man kann diese als $3 \times 3$ Drehmatrizen realisieren. Abkürzend wird die Drehgruppe des dreidimensionalen Raumes mit SO(3) oder $\mathrm{SO}_3(\mathbb R)$ oder $\mathrm{SO}(3,\mathbb R)$ bezeichnet. Das S ist die Abkürzung für speziell und bedeutet, dass die Determinante einer jeden Matrix dieser Gruppe gleich 1 ist. Durch die Determinantenbedingung werden Spiegelungen ausgeschlossen. Das O steht für orthogonal und bedeutet, dass die Matrizen Orthogonale Matrizen sind. In einer Formel geschrieben:

A ^{− 1} = A^T.

Die 3 gibt natürlich die Dimension an und das $\mathbb R$ besagt, dass die Einträge der Matrix reelle Zahlen sind.

Die Drehgruppe ist eine Lie-Gruppe. Eine Topologie bekommt die SO(3) in kanonischer Weise als Matrixgruppe und dadurch ist auch ihre Liegruppenstruktur definiert. Die SO(3) ist eine kompakte topologische Gruppe.

Die Lie-Algebra der SO(3) ist die 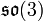$\mathfrak{so}(3)$. Sie ist eine reelle Form der Lie-Algebra sl(2,C). Letztere ergibt die auf 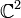$\mathbb C^2$ definierte SU(2), eine Überlagerungsgruppe vom Grad 2 zur SO(3).

Für einen beliebigen kommutativen Ring mit Eins R und eine natürliche Zahl n nennt man die Gruppe der Drehungen des Rⁿ seine spezielle orthogonale Gruppe SO(n,R).

Endliche Drehgruppen

Das Wort "Drehgruppe" wird auch dazu benutzt, um die Untergruppe der Symmetrien eines geometrischen Körpers zu bezeichnen, die aus Drehungen besteht. Diese Drehgruppe ist dann eine Untergruppe der 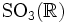$\mathrm{SO}_3(\mathbb R)$ und besteht genau aus den Drehungen, die den Körper in sich selbst überführen.

Beispielsweise ist die Symmetriegruppe des Tetraeders isomorph zur symmetrischen Gruppe auf der vierelementigen Menge der Ecken des Tetraeders, und die Untergruppe der Drehungen ist isomorph zur alternierende Gruppe A₄. Die Drehgruppe des Würfels und des Oktaeders ist isomorph zur S₄, und die Drehgruppe des Dodekaeders und des Ikosaeders ist isomorph zur A₅.