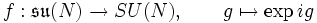- SU(2)
-
Die spezielle unitäre Gruppe der Dimension N, geschrieben SU(N), besteht aus den unitären NxN-Matrizen mit komplexen Einträgen, deren Determinante 1 beträgt.
Sie ist eine kompakte, einfache Lie-Gruppe und daher auch eine differenzierbare Mannigfaltigkeit. Ferner ist sie Untergruppe der unitären Gruppe U(N), sowie der speziellen linearen Gruppe
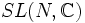 . Das Zentrum von SU(N) ist isomorph zu
. Das Zentrum von SU(N) ist isomorph zu 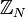 .
.Inhaltsverzeichnis
Lie-Algebra
Die zu SU(N) korrespondierende Lie-Algebra
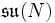 ergibt sich bei Betrachtung des Tangentialraums am Einselement der Gruppe. Sie besteht aus dem Raum aller schiefhermiteschen Matrizen mit Spur 0. Die surjektive Abbildung
ergibt sich bei Betrachtung des Tangentialraums am Einselement der Gruppe. Sie besteht aus dem Raum aller schiefhermiteschen Matrizen mit Spur 0. Die surjektive Abbildungbildet ein Element der Algebra auf die Gruppe ab.
Bedeutung in der Physik
Sie spielt eine besondere Rolle in der theoretischen Physik, da das derzeitige Standardmodell der Elementarteilchenphysik mehrere SU(N)-Symmetrien aufweist. So ist die interne Symmetriegruppe des Standardmodells durch SU(3)xSU(2)xU(1) gegeben. Darüber hinaus gibt es die näherungsweise gültige SU(3)-Symmetrie zur Klassifikation von Hadronen, die aus up-, down- und strange-Quarks bestehen. Ferner ist der kompakte Anteil der speziellen orthochronen Lorentzgruppe isomorph zu SU(2)xSU(2).
Die Gruppe SU(2) ist zugleich die sog. Doppelgruppe der gewöhnlichen Drehgruppe SO(3) im dreidimensionalen Raum.
Literatur
Lehrbücher
- Joachim Hilgert, Karl-Hermann Neeb: Lie-Gruppen und Lie-Algebren, Vieweg, 1999, ISBN 3528064323
- Nicolas Bourbaki: Lie Groups and Lie Algebras, Springer, 2002, ISBN 3540426507
- Theodor Bröcker, Tammo tom Dieck: Representations of Compact Lie Groups, Springer, 1995, ISBN 3540136789
- Walter Pfeifer: The Lie Algebras su(N), Birkhäuser, 2003, ISBN 376432418X
Artikel
- Jonathan L. Rosner: An Introduction to Standard Model Physics, TASI 1987, Scanned version from KEK
- Erhard Scholz: Introducing Groups into Quantum Theory (1926 -- 1930), math.HO/0409571
Weblinks
- Definition bei mathworld.wolfram.com (englisch)
Wikimedia Foundation.