SUSY

Die Supersymmetrie (SUSY) ist eine Symmetrie der Teilchenphysik, die Bosonen und Fermionen ineinander umwandelt. Dabei werden Teilchen, die sich unter einer SUSY-Transformation ineinander umwandeln, Superpartner genannt.

Aufgrund ihres Potenzials, offene Fragen der Teilchen- und Astrophysik zu beantworten, sind supersymmetrische Theorien insbesondere in der theoretischen Physik sehr populär. Die meisten Großen Vereinheitlichten Theorien und Superstringtheorien sind supersymmetrisch. Die minimal mögliche, mit bisherigen Erkenntnissen kompatible Erweiterung des Standardmodells der Teilchenphysik (SM), das Minimale Supersymmetrische Standardmodell (MSSM), ist der meist untersuchte Kandidat für Physik jenseits des Standardmodells (BSM-Physik). Allerdings konnte trotz vielversprechender theoretischer Argumente bis heute kein experimenteller Nachweis erbracht werden, dass Supersymmetrie tatsächlich in der Natur existiert – insbesondere wurden noch keine Superpartner bekannter Teilchen beobachtet.

Wess-Zumino Modell und MSSM

Die Supersymmetrie (in der vierdimensionalen Raum-Zeit) wurde von Juri A. Golfand und seinem Studenten Evgeni Likhtman (1971 in Moskau) sowie unabhängig von D. V. Volkov und V. P. Akulov (1972 in Charkiw/Charkow, Ukraine) eingeführt, sowie im Rahmen von Stringtheorien (zunächst nur auf der zweidimensionalen String-Weltfläche) von André Neveu, John Schwarz und Pierre Ramond. Größere Aufmerksamkeit als Modell der Elementarteilchenphysik erhielt sie erst 1974 durch die unabhängige Arbeit von Julius Wess und Bruno Zumino^[1]. Dieses heute unter dem Namen Wess-Zumino-Modell bekannte Modell beschreibt zwei skalare Bosonen, die mit sich selbst und mit einem chiralen Fermion wechselwirken. Obwohl es unrealistisch ist, ist das Wess-Zumino-Modell ein wegen seiner Einfachheit beliebtes Beispiel, an dem sich wichtige Eigenschaften supersymmetrischer Feldtheorien zeigen.

Das erste mit den bisherigen experimentellen Beobachtungen verträgliche supersymmetrische Modell, das Minimale Supersymmetrische Standardmodell (MSSM), wurde 1981 von Howard Georgi und Savas Dimopoulos vorgeschlagen. Nach den Vorhersagen des MSSM liegen die Massen der bisher unbeobachteten Superpartner in dem für den 2008 in Betrieb gegangenen Teilchenbeschleuniger Large Hadron Collider (LHC) zugänglichen Bereich von 100 GeV/c² bis 1 TeV/c². Diese Massen sind im Einklang mit dem Befund, dass bis jetzt keine Superpartner beobachtet wurden, und lassen hoffen, dass am LHC Superpartner bereits bekannter Elementarteilchen nachgewiesen werden können.

Generelle Eigenschaften

Supersymmetriealgebra

Die Supersymmetrietransformationen, die Fermionen und Bosonen ineinander umwandeln, erweitern die Raumzeitsymmetrie, die Poincaré-Gruppe.

Sidney Coleman und Jeffrey Mandula hatten 1967 ^[2] unter, wie es schien, allgemein gültigen Bedingungen gezeigt, dass außer den Erzeugenden der Poincaré-Gruppe alle anderen Erzeugenden von physikalisch relevanten Symmetrien unter Poincaré-Transformationen invariant sein müssen, dass also jede größere Symmetrie eines physikalischen Modells eine Produktgruppe der Poincaré-Gruppe mit einer Gruppe sein müsse, die nichts mit der Raumzeit zu tun hat.

Nachdem aber Wess und Zumino 1974 mit ihrem Modell gezeigt hatten, dass es auch fermionische Erzeugende von Symmetrien geben kann, die sich wie Teilchen mit Spin-1/2 bei Drehungen ändern und die von Coleman und Mandula nicht bedacht worden waren, klassifizierten 1975 Rudolf Haag, Jan Łopuszański und Martin Sohnius die möglichen Symmetriealgebren mit bosonischen und fermionischen Erzeugenden.^[3].

Die einfachste supersymmetrische Erweiterung der Poincarégruppe ist im Wess-Zumino-Modell realisiert und erweitert sie um zwei Weyl-Spinoren 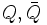$Q, \bar Q$. Die relevanten Kommutator- und Antikommutatorrelationen sind

$\{Q_{\alpha}, \bar Q_{\dot{\beta}}\} = 2({\sigma^m})_{\alpha\dot{\beta}}P_m\,, \ \ \{ Q , Q \} = \{ \bar Q ,\bar Q \} = [Q,P] = [ \bar Q, P ] = 0\,.$

Dabei bezeichnet σ^m die Pauli-Matrizen und P_m den Viererimpuls.

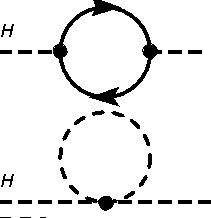
Schleifenkorrekturen durch Superpartner

Korrekturbeiträge zur Higgsmasse. Die quadratische Divergenz der Fermionenschleife im oberen Diagramm wird durch das untere Diagramm eines skalaren Superpartners kompensiert.

Die Existenz zusätzlicher Elementarteilchen liefert zusätzliche Beiträge zu den Schleifenkorrekturen für beobachtbare physikalische Parameter. Besitzen Superpartner außer dem Spin exakt gleiche Quantenzahlen, so sind die Schleifenkorrekturen identisch im Betrag, unterscheiden sich jedoch (aufgrund des unterschiedlichen Spins) im Vorzeichen. Die Korrekturen addieren sich zu Null. In gebrochenen SUSY-Modellen, insbesondere in spontan gebrochenen Modellen, addieren sich die Korrekturen nicht notwendigerweise zu Null, liefern aber oft vergleichsweise kleinere Effekte.

Die (teilweise) Kompensation der Schleifenkorrekturen durch Superpartner hat zwei interessante Effekte:

• Supersymmetrie bietet eine Möglichkeit zur Lösung des Natürlichkeitsproblems (engl. Naturalness problem oder fine-tuning problem), bei dem mit der Energieskala quadratisch divergente Schleifendiagramme zu störend großen Korrekturbeiträgen zur renormierten Masse des Higgs-Bosons führen: Zu jedem quadratisch divergenten Korrekturterm existiert ein äquivalenter Term des jeweiligen Superpartners mit entgegengesetztem Vorzeichen. Die problematischen Korrekturen addieren sich zu Null.
• Im Gegensatz zum Standardmodell ist in spontan gebrochenen (oder ungebrochenen) SUSY-Theorien der Erwartungswert der Energiedichte im feldfreien Raum endlich. Somit scheint es einfacher, die Gravitation, in der die Energiedichte Quelle für das Gravitationsfeld ist, in ein quantentheoretisches Modell einzubeziehen.

Dunkle Materie

Hauptartikel: Dunkle Materie

Um nicht in Widerspruch zu experimentellen Ergebnissen zu geraten, muss man annehmen, dass Zerfallsprozesse von Superpartnern in Standardmodellteilchen (ohne einen weiteren Superpartner als Zerfallsprodukt) stark unterdrückt oder unmöglich sind (R-Parität). Dadurch ist das leichteste supersymmetrische Partnerteilchen (LSP) praktisch stabil. Da nach aktuellen kosmologischen Modellen in Frühphasen des Universums Teilchen beliebiger Masse erzeugt werden können, stellt ein elektrisch neutrales LSP - etwa das leichteste Neutralino - einen Kandidaten als Erklärung für Dunkle Materie dar^[4].

Ausgewählte Aspekte der Supersymmetrie

MSSM: Minimales Supersymmetrisches Standardmodell

Hauptartikel: MSSM

Das MSSM ist die (im Sinne der Teilchenzahl) kleinste Möglichkeit, ein realistisches supersymmetrisches Teilchenphysikmodell aufzubauen. Das MSSM erweitert das SM um ein zusätzliches Higgs-Dublett und SUSY-Partnerteilchen für alle Teilchen des Modells, wobei kein expliziter Mechanismus angegeben wird, der begründet, warum die neuen Teilchen andere Massen besitzen als ihre Standardmodellpartner. Statt dessen werden alle supersymmetriebrechenden Terme, die renormierbar, eichinvariant und R-paritätserhaltend sind, explizit mit zunächst unbekannten Kopplungskonstanten in das Modell aufgenommen.

Vereinheitlichte Theorien

Hauptartikel: Große Vereinheitlichte Theorie

Die Existenz der neuen Teilchen ab einer Masse von 100 GeV bis 1 TeV beeinflusst das Running, d. h. die Energieabhängigkeit der Parameter („Kopplungskonstanten“), die die Stärke der drei im Standardmodell vorkommenden Wechselwirkungen charakterisieren, so dass sie sich bei extrem hohen Energien von 10¹⁶GeV einem gemeinsamen Wert nähern. Im üblichen Standardmodell treffen sie aber nur fast an einem Punkt zusammen, während supersymmetrische Theorien einen sehr viel genaueren „Vereinigungspunkt“ liefern^[5]. Dies wird manchmal als ein Hinweis auf vereinheitlichte Theorien interpretiert, also auf Theorien, in denen die drei Wechselwirkungen des Standardmodells analog der elektrischen und magnetischen Wechselwirkung nur verschiedene Effekte einer einzigen übergeordneten Wechselwirkung sind.

Supergravitation

Hauptartikel: Supergravitation

Die um die SUSY-Generatoren erweiterten Raumzeitsymmetrien sind zunächst (wie auch im Standardmodell) globale Symmetrien. Deklariert man SUSY zu einer lokalen Symmetrie, so erzwingt dies zwei neue Teilchen: Das Spin-3/2 Gravitino und das Spin-2 Graviton, von dem erwartet wird, das Wechselwirkungsteilchen der Gravitation zu sein^[6]. Daher werden lokale SUSY-Theorien auch Supergravitation (SUGRA) genannt. Supergravitation besitzt gegenüber lokaler Raumzeitsymmetrie im Standardmodell (die nicht renormierbar ist) zwei potentielle Vorteile, die insbesondere in der Anfangsphase supersymmetrischer Ansätze die Hoffnung nährten, dass SUSY einen möglichen Mechanismus für eine Theorie der Quantengravitation liefert:

• Nach der Relativitätstheorie ist die totale Energiedichte des Raumes ein Quellterm für Gravitation. Im Standardmodell der Teilchenphysik ist der Erwartungswert der Energiedichte jedoch bereits im Vakuum unendlich. In supersymmetrischen Theorien ist die Vakuumenergiedichte endlich (im Fall der ungebrochenen Supersymmetrie sogar exakt Null).
• Der unterschiedliche Spin von Graviton und Gravitino könnte dazu führen, dass sich nichtrenormierbare Terme kompensieren und die Theorie renormierbar wird.

Bis heute ist es – mit potentieller Ausnahme von Superstringansätzen, die jedoch über einfache Supersymmetrie hinausgehen – nicht gelungen, eine widerspruchsfreie Theorie der Supergravitation aufzustellen. SUGRA könnte allerdings eine effektive Theorie unterhalb der Planck-Skala sein: SUGRA ist ein möglicher Mechanismus für spontane Supersymmetriebrechung. In manchen Modellen ist der Nachweis des Gravitinos an zukünftigen Beschleunigerexperimenten wie dem LHC denkbar^[7].

Weiterführende Informationen

Siehe auch

• Hierarchieproblem

Literatur

• Ian J. Aitchison: Supersymmetry in particle physics - an elementary introduction. Cambridge Univ. Pr., Cambridge 2007, ISBN 978-0-521-88023-7
• Sergio Ferrara, Rudolf M.Mössbauer: Searching for the superworld. World Scientific, Singapore 2007, ISBN 978-981-270-018-6
• Michael Dine: Supersymmetry and string theory - beyond the standard model. Cambridge Univ. Press, Cambridge 2007, ISBN 0-521-85841-0
• John Terning: Modern supersymmetry - dynamics and duality. Clarendon Press, Oxford 2007, ISBN 978-0-19-856763-9
• Jonathan A. Bagger: Supersymmetry, supergravity and supercolliders. World Scientific, Singapore 1999, ISBN 981-02-3816-9
• Luisa Cifarelli (et al.): Properties of SUSY particles. World Scientific, Singapore 1993, ISBN 981-02-1424-3

Weblinks

• A Supersymmetry Primer by S.P. Martin. (Sehr beliebte englischsprachige Quelle zum Thema. Ausgehend von bekannter Quantenfeldtheorie wird über das Wess-Zumino Modell das MSSM motiviert und begründet. Phänomenologische Aspekte des MSSM und mögliche Erweiterungen werden kurz behandelt)

Einzelnachweise

1. ↑ J. Wess, B. Zumino: Supergauge transformations in four dimensions. in: Nuclear physics. B. Amsterdam 70.1974, 39-50. ISSN 0550-3213
2. ↑ Sidney Coleman, Jeffrey Mandula: All possible symmetries of the S-matrix., Physical Review, Bd.159, 1967, S. 1251-1256. ISSN 0031-899X
3. ↑ Haag, Lopuszanki, Sohnius: All possible generators of supersymmetries of the S-matrix. in: Nuclear physics. B. Amsterdam 88.1975, 257. ISSN 0550-3213
4. ↑ Siehe z.B. D. Hooper, T. Plehn: Supersymmetric Dark Matter - How light can the LSP be? in: Physics letters. B. Amsterdam 562.2003, 18-27. ISSN 0031-9163
5. ↑ U. Amaldi, W. de Boer, H. Fürstenau, Comparison of Grand Unified Theories with electroweak and strong coupling constants measured at LEP, Physics Letters Bd. 260, 1991, S.447
6. ↑ Takeo Moroi: Effects of the Gravitino on the Inflationary Universe.
7. ↑ Nanopoulos u. a.: Light-Gravitino Production at Hadron Colliders. in: Physical review. D. Melville 57.1998, 373-382. ISSN 0556-2821