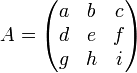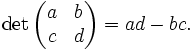Sarrusregel

In der linearen Algebra ist die Regel von Sarrus (oder sarrussche Regel) ein Schema, mit dem die Determinante einer 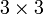$3\times3$-Matrix leicht von Hand berechnet werden kann. Sie ist benannt nach dem französischen Mathematiker Pierre Frederic Sarrus. Es handelt sich um einen Spezialfall der Leibniz-Formel.

Für die $3\times3$-Matrix

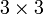$A = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}$

besteht die Determinante aus 6 Summanden von je 3 Faktoren, die leicht mit dem folgenden Schema ermittelt werden können.

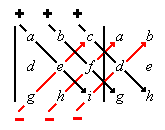
Dabei schreibt man die ersten beiden Spalten der Matrix rechts neben die Matrix und bildet Produkte von je 3 Zahlen, die durch die schrägen Linien verbunden sind. Dann werden die nach unten verlaufenden Produkte addiert und davon die nach oben verlaufenden Produkte subtrahiert. Man erhält auf diese Weise die Determinante von A:

det(A) = aei + bfg + cdh − gec − hfa − idb.

Für 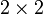$2\times2$-Matrizen gilt die ähnlich aussehende Regel

$\det \begin{pmatrix} a & b \\ c & d \end{pmatrix} = ad - bc.$

Für größere Determinanten kann man kein so einfaches Schema angeben, da die Anzahl der Summanden schnell wächst: Bereits für eine 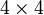$4\times4$-Matrix erhielte man mit der Sarrus-Regel nur 8 der 24 Summanden. Hier wendet man häufig den Laplaceschen Entwicklungssatz an, da die Komplexität der Leibniz-Formel zu schnell wächst.

Literatur

• Gerd Fischer: Analytische Geometrie. 4-te Auflage, Vieweg 1985, ISBN 3-528-37235-4, S.145

Weblinks

• Regel von Sarrus (engl.) auf Planetmath
• Regel von Sarrus