Satz von Löwenheim und Skolem

Das Löwenheim-Skolem-Theorem besagt, dass eine Menge von Aussagen der Prädikatenlogik erster Stufe, die in einem Modell mit einer überabzählbar unendlich großen Domäne erfüllt ist, immer auch in einem Modell mit einer abzählbar unendlich großen Domäne erfüllt ist.

Erläuterung und Konsequenzen

Einige wichtige Begriffe des Satzes seien kurz erläutert: Ein Modell repräsentiert (in einer mathematisch beschreibbaren Form) bestimmte Umstände, die bestehen, wenn bestimmte Aussagen wahr sind. Man sagt dann, dass das Modell die Aussagen erfüllt. Die Domäne (auch Individuenbereich oder Träger genannt) enthält diejenigen Individuen, deren Existenz in dem Modell vorausgesetzt ist. Eine Menge heißt abzählbar unendlich, wenn sie so groß ist wie die Menge der natürlichen Zahlen. Eine überabzählbar unendliche Menge ist größer als die Menge der natürlichen Zahlen. Dabei ist eine Menge A mindestens so groß wie eine Menge B, wenn es eine injektive Funktion von B nach A gibt.

Ein im Vergleich zu dem Satz von Löwenheim-Skolem leicht zu beweisendes Resultat der Modelltheorie besagt, wenn eine Menge von Aussagen durch ein bestimmtes unendliches Modell erfüllt ist, so ist sie immer auch durch ein Modell mit einer größeren Domäne erfüllt. Zusammen mit dem Satz von Löwenheim-Skolem ergibt sich, dass eine Aussagenmenge, die überhaupt ein unendliches Modell hat, immer auch ein Modell mit einer abzählbar unendlich großen Domäne hat. Aus dem Satz folgt u.a., dass mittels Prädikatenlogik erster Stufe keine unendlichen Strukturen (insbesondere die natürlichen Zahlen) in bis zur Isomorphie eindeutiger Weise beschrieben werden können.

Geschichte

Der Satz wird zuerst von Leopold Löwenheim im Jahr 1915 bewiesen. Historisch gesehen handelt es sich wohl um das erste nicht-triviale Resultat der Modelltheorie. Aus Löwenheims Beweis folgen eine ganze Reihe interessanter Konsequenzen, die zum Teil von ihm selbst nicht gesehen worden sind. So zeigt Löwenheim ebenfalls:

• dass der einstellige Prädikatenkalkül erster Stufe entscheidbar ist,
• dass der Prädikatenkalkül erster Stufe auf den zweistelligen Prädikatenkalkül erster Stufe reduzierbar ist
• dass es erfüllbare Aussagen des Prädikatenkalküls zweiter Stufe gibt, die kein abzählbares Modell haben.

1920 verallgemeinert Albert Thoralf Skolem Löwenheims Resultat. Zum einen zeigt er, dass die Menge von Aussagen selbst abzählbar unendlich groß sein darf (während Löwenheim sein Theorem nur für einzelne Aussagen bewiesen hatte) zum anderen beweist er, dass eine überabzählbare Domäne sich immer unter Bewahrung der Erfüllungsrelation auf eine abzählbare Subdomäne einschränken lässt. (Für letzteres muss jedoch das Auswahlaxiom vorausgesetzt werden.) Skolem macht bei seinem Beweis Gebrauch von der berühmten Skolemform.

Der Satz wird in modernen Darstellungen der Modelltheorie meist als Korollar aus dem Vollständigkeitssatz der Prädikatenlogik präsentiert. Zu Zeiten Löwenheims und Skolems war die Vollständigkeit noch nicht bewiesen, so dass sie auf diesem Resultat nicht aufbauen konnten. Umgekehrt gilt, dass zumindest Skolems Beweis leicht in einen Vollständigkeitsbeweis hätte umgeformt werden können.

Das Skolem-Paradoxon

Nimmt man an, dass die Zermelo-Fraenkel-Mengenlehre widerspruchsfrei ist, so hat jedes endliche axiomatische System aus der Zermelo-Fraenkel-Mengenlehre ein abzählbares Modell. Dies folgt aus dem Löwenheim-Skolem-Theorem und wurde weiter oben schon erläutert. Jedoch kann in der Zermelo-Fraenkel-Mengenlehre ein endliches axiomatisches System Ψ angegeben werden, sodass die Existenz einer überabzählbaren Menge folgt.

Der Widerspruch löst sich jedoch dann auf, wenn man sich klar macht, was Abzählbarkeit auf ein Modell bezogen bedeutet. Sei M ein System von Ψ. Ist weiter 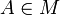$A \in M$ eine Menge, die im Modell von M überabzählbar ist, so bedeutet dies, dass es in diesem Modell keine Surjektion 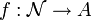$f : \mathcal{N} \rightarrow A$ gibt. Die Menge 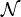$\mathcal{N}$ bezeichnet die zu dem Modell M relativierte Menge der natürlichen Zahlen. Jedoch bedeutet dies nicht, dass die Menge M selbst überabzählbar ist. Nach dem Gödelschen Unvollständigkeitssatz vermag kein Axiomensystem der Mengenlehre das inhaltliche Operieren mit Mengen adäquat zu beschreiben, d.h. es hat stets Modelle, die von den eigentlichen intendierten Mengen wesentlich verschieden sind.

Skolem selbst hat das Resultat als paradox betrachtet, daher rührt der Ausdruck „Skolem'sches Paradoxon“.

Hilary Putnams modelltheoretisches Argument

Das Löwenheim-Skolem-Theorem wurde von dem Philosophen und Logiker Hilary Putnam auf repräsentationale Systeme angewandt, um zu zeigen: die Wahrheitsbelegung in allen möglichen Welten fixiert die Referenz sprachlicher Ausdrücke nicht. ^[1]

Weblinks

• Timothy Bays: „Skolem's Paradox“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
• Geschichte der Logik von 1900 bis 1935 (Online-Version als PDF; 652 KB; englisch)

Quellenangaben

1. ↑ Reason Truth and History. Cambridge: Cambridge University Press 1981. Realism and Reason. Cambridge: Cambridge University Press 1983.