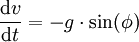- Schulerperiode
-
Als Schuler-Periode bezeichnet man die Schwingungsdauer von etwa 84,4 Minuten. Die Untersuchungen gehen zurück auf Maximilian Schuler, der den Einfluss der Schlingerbewegungen eines Schiffes auf einen Kreiselkompass zu minimieren suchte.
Beispiel für ihr Auftreten sind:
- Schwingungsdauer eines Pendels mit der Länge des Erdradius 6.370 km
- Umlaufzeit eines Satelliten um die Erde auf Meereshöhe
- Gesamtzeit, die ein Stein benötigen würde, bis er zum Startpunkt zurückkommt, falls er durch einen die Erde durchschneidenden, luftleeren Tunnel fällt. Wenn die Tunnelachse nicht identisch mit der Rotationsachse der Erde ist, treten Seitenkräfte auf (Corioliskraft), die beispielsweise durch Schienen aufgenommen werden müssen.
Anwendung und Herleitung
Ein Pendel, wie es zum Beispiel bei einem Kreiselkompass verwendet wird, legt die Lotrichtung fest. Beschleunigungen entlang der Pendelachse sind ohne Einfluss. Bewegungen senkrecht dazu versetzen es in heftige Schwingungen, die eine Bestimmung des Lots unmöglich machen. Ein Sonderfall ist ein Pendel mit der Länge des Erdradius von 6.370 km. Es bleibt in Ruhe, wenn es entlang der Erdoberfläche bewegt wird. In der Praxis konstruiert man das System so, dass die Eigenschwingfrequenz mit der Schuler-Periode zusammenfällt.
Die Schuler-Periode beobachtet man auch bei einem fest auf der Erde montierten inertialen Navigationssystem (INS). Eine Drehung der Erde um den Winkel φ dreht auch das INS auf der Erdoberfläche und übt ein Drehmoment aus. Die auf die gekippte Achse des INS ausgeübte Beschleunigung dv/dt (v: Geschwindigkeit; g: Erdbeschleunigung) beträgt:
bzw. für kleine Winkeländerungen:
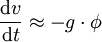 .
.
Die Winkelgeschwindigkeit
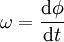 der Erde beträgt (R: Radius):
der Erde beträgt (R: Radius):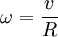 .
.
Daraus folgt gemäß der Schwingungsgleichung die Schwingungsdauer T:
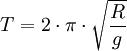 .
.
Siehe auch
Weblinks
- Anwendungen (englisch)
Wikimedia Foundation.