- Schur-Normalform
-
In der Linearen Algebra, einem Teilgebiet der Mathematik, ist die Schur-Zerlegung (oder auch Schursche Normalform genannt) eine wichtige Matrix-Zerlegung, genauer ein Trigonalisierungsverfahren.
Sie ist benannt nach dem Mathematiker Issai Schur.
Inhaltsverzeichnis
Definition
A sei eine quadratische Matrix mit Einträgen aus
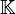 (also
(also 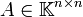 , wobei
, wobei 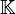 entweder für
entweder für  oder für
oder für  steht). Zerfällt das charakteristische Polynom von A über
steht). Zerfällt das charakteristische Polynom von A über 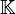 in Linearfaktoren, so existiert eine unitäre Matrix
in Linearfaktoren, so existiert eine unitäre Matrix 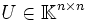 , sodass
, sodass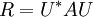 (U * ist die zu U adjungierte Matrix)
(U * ist die zu U adjungierte Matrix)
eine obere Dreiecksmatrix ist.
Bemerkungen
- Da R eine obere Dreiecksmatrix ist, kann sie als Summe einer Diagonalmatrix D und einer strikten oberen Dreiecksmatrix N dargestellt werden (
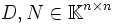 ):
):
- R = D + N
- Es gilt dann:
- D ist eindeutig bis auf die Reihenfolge der Diagonalelemente und wird als der Diagonalanteil der Schur-Zerlegung bezeichnet.
- N ist nilpotent, im Allgemeinen nur bezüglich ihrer Frobeniusnorm eindeutig und wird der nilpotente Anteil der Schur-Zerlegung genannt.
- Die Frobeniusnorm von N ist genau dann 0, wenn A normal ist.
- Wegen der Ähnlichkeit der Ausgangsmatrix A und der oberen Dreiecksmatrix R sitzen in der Diagonale von R die Eigenwerte von A.
- Ist A eine normale Matrix, dann ist R sogar eine Diagonalmatrix und die Spaltenvektoren von U sind die Eigenvektoren von A. Die Schur-Zerlegung von A wird dann als Spektralzerlegung von A bezeichnet.
- Wenn A positiv definit ist, dann ist die Schur-Zerlegung von A dasselbe wie die Singulärwertzerlegung von A.
Konstruktion einer Schur-Zerlegung
Sei
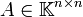 . Zunächst muss ein Eigenwert λ1 und ein entsprechender Eigenvektor v1 zu A gefunden werden. Nun werden n − 1 Vektoren w2,...,wn gewählt, so das v1,w2,...,wn eine orthonormale Basis in
. Zunächst muss ein Eigenwert λ1 und ein entsprechender Eigenvektor v1 zu A gefunden werden. Nun werden n − 1 Vektoren w2,...,wn gewählt, so das v1,w2,...,wn eine orthonormale Basis in 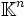 bilden. Diese Vektoren bilden die Spalten einer Matrix V1.
bilden. Diese Vektoren bilden die Spalten einer Matrix V1. 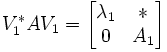 ,wobei A1 eine
,wobei A1 eine  Matrix ist.
Matrix ist.Nun wird dieser Vorgang für A1 wiederholt. Es entsteht eine unitäre Matrix V2 mit:
 , wobei A2 eine
, wobei A2 eine 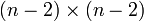 Matrix ist.
Matrix ist.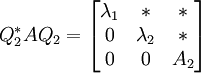 , wobei
, wobei 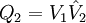 mit
mit 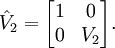
Die gesamte Prozedur wird n-mal wiederholt, bis die Matrizen
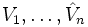 vorliegen.
vorliegen. ist eine unitäre Matrix, U eine obere Dreiecksmatrix und somit ist A = QUQ * die Schur-Zerlegung der Matrix A.
ist eine unitäre Matrix, U eine obere Dreiecksmatrix und somit ist A = QUQ * die Schur-Zerlegung der Matrix A.Beispiel
Betrache beispielsweise die Matrix
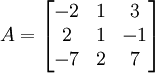 mit den Eigenwerten
mit den Eigenwerten 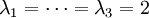 (die Matrix ist nicht diagonaliserbar, weil die Dimension des mit diesem Eigenwert assoziierten Eigenraums 2 beträgt).
(die Matrix ist nicht diagonaliserbar, weil die Dimension des mit diesem Eigenwert assoziierten Eigenraums 2 beträgt).Wir wählen als Basis für den Anfang die Standard-Basis
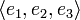 , wobei ej den j-ten Einheitsvektor bezeichnet.
, wobei ej den j-ten Einheitsvektor bezeichnet.Für A1 = A bestimmen wir einen Eigenvektor zu 2, z. B.
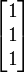 mit Darstellung
mit Darstellung  und ergänzen ihn zu einer linear unabhängigen Basis, z. B.
und ergänzen ihn zu einer linear unabhängigen Basis, z. B. 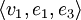 . Aus dieser neuen Basis erzeugen wir die Basistransformtion V1 = (v1 | e1 | e3) und berechnen
. Aus dieser neuen Basis erzeugen wir die Basistransformtion V1 = (v1 | e1 | e3) und berechnen  daraus lässt sich ablesen, dass
daraus lässt sich ablesen, dass 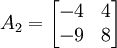 .
.Für A2 bestimmen wir einen Eigenvektor zu 2, z. B.
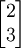 mit Darstellung
mit Darstellung 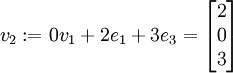 und ergänzen ihn zu einer linear unabhängigen Basis, z. B.
und ergänzen ihn zu einer linear unabhängigen Basis, z. B. 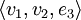 . Aus dieser neuen Basis erzeugen wir die Basistransformation V2 = (v1 | v2 | e3) und berechnen
. Aus dieser neuen Basis erzeugen wir die Basistransformation V2 = (v1 | v2 | e3) und berechnen 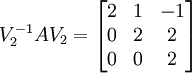 .
.Wie oben gezeigt, kann die Basis beliebig gewählt werden, allerdings wird die Sache sehr einfach und interessant, wenn die Wahl der Standardbasis durchgezogen wird (sofern möglich). Dadurch ändern sich die vorherigen Schritte wie folgt:
Für A1 = A bestimmen wir einen Eigenvektor zu 2, z. B.
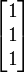 mit Darstellung
mit Darstellung 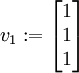 und ergänzen ihn zu einer linear unabhängigen Basis, z. B.
und ergänzen ihn zu einer linear unabhängigen Basis, z. B.  . Aus dieser neuen Basis erzeugen wir die Basistransformtion V1 = (v1 | e2 | e3) und berechnen
. Aus dieser neuen Basis erzeugen wir die Basistransformtion V1 = (v1 | e2 | e3) und berechnen 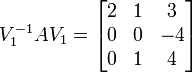 daraus lässt sich ablesen, dass
daraus lässt sich ablesen, dass 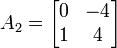 .
.Für A2 bestimmen wir einen Eigenvektor zu 2, z. B.
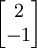 mit Darstellung
mit Darstellung  und ergänzen ihn zu einer linear unabhängigen Basis, z. B.
und ergänzen ihn zu einer linear unabhängigen Basis, z. B. 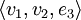 . Aus dieser neuen Basis erzeugen wir die Basistransformtion V2 = (v1 | v2 | e3) und berechnen
. Aus dieser neuen Basis erzeugen wir die Basistransformtion V2 = (v1 | v2 | e3) und berechnen 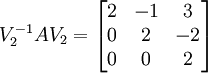 .
.Hier ist die Berechnung der Darstellung der Vektoren in der richtigen Basis sozusagen intuitiv und somit auch weniger fehleranfällig, zudem ist die finale Basistransformation hier V2 auch eine Dreiecksmatrix.
Mit dem Gram-Schmidtschen Orthogonalisierungsverfahren kann die erhaltene Basistransformationsmatrix zu einer unitären Matrix gemacht werden, wie verlangt.
Siehe auch
Weblinks
- LP - Lemma von Schur, u.a. Beweis des Lemmas, in: Numerische Mathematik I - Funktionalanalytische Grundlagen.
Wikimedia Foundation.
