- Schursches Lemma
-
Das Lemma von Schur, benannt nach Issai Schur, beschreibt die Homomorphismen zwischen irreduziblen Moduln. Es besagt, dass jeder solche Homomorphismus außer dem Nullhomomorphismus ein Isomorphismus ist.
Das Lemma von Schur in der modultheoretischen Fassung lautet (R sei ein Ring mit 1):
Es seien M, N einfache R-Linksmoduln. Dann gilt:
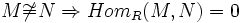
- EndR(M) ist ein Schiefkörper.
In der darstellungstheoretischen Fassung lautet das Lemma von Schur (G sei eine endliche Gruppe, K ein Körper):
Es seien
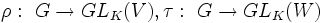 irreduzible Darstellungen von G. Dann gilt:
irreduzible Darstellungen von G. Dann gilt:- Es sei
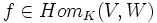 mit
mit 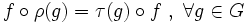 . Dann gilt: f=0 oder f ist bijektiv (und in diesem Fall sind ρ und τ äquivalent).
. Dann gilt: f=0 oder f ist bijektiv (und in diesem Fall sind ρ und τ äquivalent). - Z(ρ) ist ein Schiefkörper.
Die Aussage 2. gilt auch in der Umkehrung, so dass Z(ρ) ein Schiefkörper ist, genau dann wenn die Darstellung ρ irreduzibel ist.
Aufgrund des Zusammenhangs von Darstellungen von G über K und KG-Moduln besagen beide Fassungen das gleiche.
Wikimedia Foundation.
