Schwingers Variationsansatz

Dieser Artikel wurde aufgrund von inhaltlichen Mängeln auf der Qualitätssicherungsseite des Portals Physik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Physik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Hilf mit, die inhaltlichen Mängel dieses Artikels zu beseitigen, und beteilige dich an der Diskussion.

Schwingers Variationsansatz, nach seinem Entwickler Julian Seymour Schwinger benannt, ist ein Formalismus der Quantenfeldtheorie. In diesem Formalismus ist die Quantenwirkung ein Operator, anders als in der Pfadintegralformulierung, in der die Wirkung ein klassisches Funktional ist.

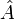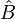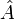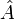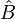Nehmen wir an, wir haben einen vollständigen Satz kommutierender (oder, für Fermionen, antikommutierender) Operatoren $\hat{A}$ und zweiten anderen Satz $\hat{B}$. Sei |A> Eigenzustand von $\hat{A}$ mit Eigenwert A und entsprechend für |B>. Es gibt eine Unbestimmtheit in der Phase, aber darauf kann in der Quantenwirkung S_AB, zugeordnet zu $\hat{A}$ und $\hat{B}$, geachtet werden.

Nehmen wir an, wir haben nicht nur ein Modell der Quantenmechanik oder Quantenfeldtheorie, sondern derer eine ganze Familie, die sich leicht unterscheiden. Damit sind |A> und |B> "unterschiedlich" für jedes Modell innerhalb der Familie. Die Quantenwirkung S_AB variiert ebenfalls leicht. Diese Variation sei durch einen Parameter quantifiziert. Schwinger's Variationsprinzip besagt nun

δ < A | B > = i < A | δS_AB | B > ,

wobei die Ableitung δ als Ableitung nach dem Parameter aufzufassen ist.

Literatur

• Beschreibung von Schwingers Arbeiten im historischen Kontext