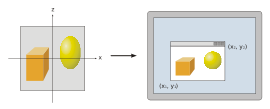
Screenmapping

Eine Computergrafik-Pipeline, auch Rendering-Pipeline oder einfach Grafikpipeline, ist eine Modellvorstellung in der Computergrafik, die beschreibt, welche Schritte ein Grafiksystem zum Rendern, also zur Darstellung einer 3D-Szene auf einem Bildschirm, durchführen muss. Da diese Schritte sowohl von der Soft- und Hardware als auch von den gewünschten Darstellungseigenschaften abhängen, gibt es keine allgemein gültige Grafikpipeline. Zur Ansteuerung von Grafikpipelines werden üblicherweise Grafik-APIs wie Direct3D oder OpenGL verwendet, die die zugrundeliegende Hardware abstrahieren und dem Programmierer viele Aufgaben abnehmen.

Das Modell der Grafikpipeline findet üblicherweise beim Echtzeitrendern Anwendung. Oft sind hier die meisten Schritte der Pipeline in Hardware implementiert, was besondere Optimierungen ermöglicht. Die Bezeichnung „Pipeline“ wird in einem ähnlichen Sinn wie die Pipeline bei Prozessoren verwendet: die einzelnen Schritte der Pipeline laufen zwar parallel ab, sind jedoch solange blockiert, bis der langsamste Schritt beendet wurde. Auf Techniken wie Raytracing, die vor allem in der realistischen Bildsynthese verwendet werden, ist das Grafikpipeline-Modell nicht anwendbar.

Aufbau

Eine Grafikpipeline lässt sich in drei große Schritte aufteilen: Anwendung, Geometrie und Rasterung.^[1]

Anwendung

Der Anwendungsschritt wird von der Software ausgeführt, er lässt sich daher nicht in pipelineartig ausgeführte Einzelschritte aufteilen. Es ist jedoch möglich, ihn auf Mehrkernprozessoren oder Mehrprozessorsystemen zu parallelisieren. Im Anwendungsschritt werden Änderungen an der Szene vorgenommen, wie sie zum Beispiel aufgrund der Benutzerinteraktion mittels Eingabegeräten oder bei einer Animation nötig sind. Die neue Szene mit allen ihren Primitiven – meist Dreiecke, Linien und Punkte – wird dann an den nächsten Schritt der Pipeline weitergeleitet.

Beispiele für Aufgaben, die typischerweise vom Anwendungsschritt übernommen werden, sind Kollisionserkennung, Animation, Morphing und Beschleunigungstechniken mittels räumlicher Unterteilungsschemas.

Geometrie

Der Geometrieschritt, der für den Großteil der Operationen mit Polygonen und deren Eckpunkten (Vertices) verantwortlich ist, lässt sich in folgende fünf Aufgaben unterteilen. Es hängt von der jeweiligen Implementierung ab, wie diese Aufgaben als tatsächliche, parallel ausgeführte Pipeline-Schritte organisiert werden.

Modell- und Kameratransformation

Links: Position und Richtung des virtuellen Betrachters, wie er vom Anwender definiert wurde. Rechts: Platzierung der Objekte nach der Kameratransformation. Der hellgraue Bereich ist das Sichtvolumen.

Die in der Szene angegebenen Objekte sind aus Gründen der einfacheren Modellierung oftmals in ihrem eigenen Objektkoordinatensystem (auch Modellkoordinatensystem oder lokales Koordinatensystem) angegeben. Um diesen Objekten Koordinaten im Weltkoordinatensystem oder globalen Koordinatensystem der gesamten Szene zuzuweisen, werden die Objektkoordinaten mittels Translation, Rotation oder Skalierung transformiert. Dies geschieht durch Multiplikationen der entsprechenden Transformationsmatrizen. Außerdem können aus einem Objekt mehrere unterschiedlich transformierte Kopien gebildet werden, etwa ein Wald aus einem Baum; diese Technik wird Instancing genannt.

Neben den Objekten definiert die Szene auch eine virtuelle Kamera oder einen Betrachter, der die Position und Blickrichtung angibt, aus der die Szene gerendert werden soll. Um die spätere Projektion und das Clipping zu vereinfachen, wird die Kamera und die Szene so transformiert, dass sich die Kamera am Ursprung befindet, mit Blickrichtung entlang der z-Achse. Das resultierende Koordinatensystem wird Kamera-Koordinatensystem genannt und die Transformation Kameratransformation.

Aus Effizienzgründen werden die Modell- und die Kameratransformation üblicherweise in eine Transformationsmatrix zusammengefasst, sodass die Weltkoordinaten übergangen werden. Außerdem sind weitere, aufwändigere Transformationen wie Vertex Blending möglich. Frei programmierbare Vertex-Shader, die die Geometrie verändern, können ebenfalls ausgeführt werden.

Beleuchtung

Oft enthält eine Szene an verschiedenen Positionen platzierte Lichtquellen, um die Beleuchtung der Objekte realistischer erscheinen zu lassen. In diesem Fall wird für jeden Vertex anhand der Lichtquellen und den zum entsprechenden Dreieck gehörenden Materialeigenschaften sowie ihrer Textur eine Farbe berechnet. Im späteren Rasterungsschritt werden die Eckpunktfarben eines Dreiecks über dessen Fläche interpoliert.

Projektion

Der Projektionsschritt transformiert das Sichtvolumen in einen Würfel mit den Eckpuntkoordinaten (–1, –1, –1) und (1, 1, 1); gelegentlich werden auch andere Zielvolumen verwendet. Dieser Schritt wird Projektion genannt, obwohl er ein Volumen in ein anderes Volumen transformiert, da die resultierenden z-Koordinaten nicht im Bild gespeichert werden, sondern lediglich beim Z-Buffering im späteren Rasterungsschritt Anwendung finden. Bei einer perspektivischen Abbildung wird eine Zentralprojektion verwendet. Um die Anzahl der dargestellten Objekte zu begrenzen, werden zwei zusätzliche Clipping Planes verwendet; das Sichtvolumen ist hier also ein Pyramidenstumpf (Frustum). Die seltener verwendete Parallelprojektion kann als Spezialfall der Zentralprojektion betrachtet werden. Die Transformation des Frustums in einen Würfel geschieht mittels 4×4-Matrizen (homogene Matrizen). Die so transformierten Punkte liegen in Clipping-Koordinaten vor.

Clipping von Primitiven gegen den Würfel. Das blaue Dreieck wird verworfen, während das orangene Dreieck geclippt wird, wobei zwei neue Vertices erzeugt werden.

Clipping

Nur die Primitive, die sich innerhalb des nun würfelförmigen Sichtvolumens befinden, müssen auch tatsächlich gerastert werden. Primitiven, die sich vollständig außerhalb des Sichtvolumens befinden, werden verworfen; dies wird Frustum Culling genannt. Weitere Culling-Verfahren wie Backface Culling, die die Zahl der zu berücksichtigenden Primitiven reduzieren, können theoretisch in einem beliebigen Schritt der Grafikpipeline ausgeführt werden. Primitven, die sich nur teilweise im Innern des Würfels befinden, müssen gegen den Würfel geclippt werden. Der Vorteil des vorherigen Projektionsschrittes liegt darin, dass das Clipping stets gegen den gleichen Würfel stattfindet. Nur die – eventuell geclippten – Primitiven, die sich innerhalb des Sichtvolumens befinden, werden an den nächsten Schritt weitergeleitet.

Window-Viewport-Transformation

Window-Viewport-Transformation

Um das Bild an einem beliebigen Zielbereich (Viewport) des Bildschirms auszugeben, muss eine weitere Transformation, die Window-Viewport-Transformation, angewandt werden. Dabei handelt es sich um eine Verschiebung, gefolgt von einer Skalierung. Die resultierenden Koordinaten sind die Gerätekoordinaten des Ausgabegeräts. Die z-Koordinaten bleiben von dieser Transformation unberührt.

Rasterung

Im Rasterungsschritt werden alle Primitiven gerastert, also die zu ihnen gehörenden Pixel eingefärbt. Dazu ist es nötig, bei überlappenden Polygonen das jeweils sichtbare, also näher am Betrachter liegende, zu ermitteln. Für diese sogenannte Verdeckungsberechnung wird üblicherweise ein Z-Buffer verwendet. Die Farbe eines Pixels hängt von der Beleuchtung, Textur und anderen Materialeigenschaften des sichtbaren Primitivs ab und wird oft anhand der Dreieckseckpunkte interpoliert. Pixel-Shader sind ebenfalls möglich.

Damit der Anwender nicht die allmähliche Rasterung der Primitiven sieht, findet Doppelpufferung statt. Die Rasterung erfolgt dabei in einem besonderen Speicherbereich. Sobald das Bild komplett gerastert wurde, wird es auf einmal in den sichtbaren Bereich des Bildspeichers kopiert.

Literatur

• Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. AK Peters, Natick, Mass. 2002, ISBN 1-56881-182-9
• Michael Bender, Manfred Brill: Computergrafik: ein anwendungsorientiertes Lehrbuch. Hanser, München 2006, ISBN 3-446-40434-1

Einzelnachweise

1. ↑ Tomas Akenine-Möller, Eric Haines: Real-Time Rendering, S. 11