- Semiendliche von-Neumann-Algebra
-
Die hier vorgestellte Typklassifikation teilt die in der Mathematik untersuchten von-Neumann-Algebren in Klassen ein, die man Typ nennt. Diese auf Francis J. Murray und John von Neumann zurückgehende Klassifizierung beruht auf einer Analyse der Struktur der in einer von-Neumann-Algebra enthaltenen Orthogonalprojektionen. Während beliebige von-Neumann-Algebren Bestandteile unterschiedlicher Typen haben können, ist ein Faktor immer von genau einem Typ. Daher spielen diese Begriffsbildungen bei der Untersuchung der Faktoren eine wichtige Rolle.
Inhaltsverzeichnis
Motivation
Die Grundidee besteht darin, Projektionen einer von-Neumann-Algebra
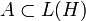 auf einem Hilbertraum H der Größe nach zu vergleichen. Ist
auf einem Hilbertraum H der Größe nach zu vergleichen. Ist 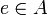 eine solche Projektion (mit Projektion ist hier immer eine Orthogonalprojektion gemeint), so gehört dazu der projizierte Raum e(H) und umgekehrt gibt es zu jedem abgeschlossenen Unterraum in H genau eine Projektion auf diesen Unterraum. Es liegt daher nahe, die Mengen e(H) zum Größenvergleich heranzuziehen. Gilt
eine solche Projektion (mit Projektion ist hier immer eine Orthogonalprojektion gemeint), so gehört dazu der projizierte Raum e(H) und umgekehrt gibt es zu jedem abgeschlossenen Unterraum in H genau eine Projektion auf diesen Unterraum. Es liegt daher nahe, die Mengen e(H) zum Größenvergleich heranzuziehen. Gilt 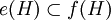 für zwei Projektionen e und f, so wird man f als die größere bezeichnen wollen. Wie bei allgemeinen Mengen kann es vorkommen, dass zwei Projektionen auf diese Weise nicht direkt miteinander vergleichbar sind, da zwischen den projizierten Räumen keine Inklusionsbeziehung besteht. Bei zwei Mengen kann man Vergleichbarkeit dadurch herstellen, dass man eine der Mengen bijektiv auf eine Teilmenge der anderen abbildet. Verfolgt man diese Analogie zwischen Mengen und Projektionen weiter, und diese Sichtweise erweist sich als sehr fruchtbar, so kommt man zwanglos zur folgenden Begriffsbildung:
für zwei Projektionen e und f, so wird man f als die größere bezeichnen wollen. Wie bei allgemeinen Mengen kann es vorkommen, dass zwei Projektionen auf diese Weise nicht direkt miteinander vergleichbar sind, da zwischen den projizierten Räumen keine Inklusionsbeziehung besteht. Bei zwei Mengen kann man Vergleichbarkeit dadurch herstellen, dass man eine der Mengen bijektiv auf eine Teilmenge der anderen abbildet. Verfolgt man diese Analogie zwischen Mengen und Projektionen weiter, und diese Sichtweise erweist sich als sehr fruchtbar, so kommt man zwanglos zur folgenden Begriffsbildung:Definition: Zwei Projektionen
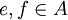 heißen äquivalent, in Zeichen
heißen äquivalent, in Zeichen 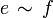 , wenn es ein
, wenn es ein 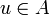 mit e = u * u und f = uu * gibt, ein solches u ist dann eine partielle Isometrie. Man sagt, e sei schwächer als f, in Zeichen
mit e = u * u und f = uu * gibt, ein solches u ist dann eine partielle Isometrie. Man sagt, e sei schwächer als f, in Zeichen 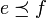 , falls es eine Projektion
, falls es eine Projektion 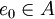 gibt mit
gibt mit 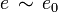 und
und 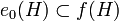 .
.Äquivalenz und Vergleichbarkeit hängen von der von-Neumann-Algeba A ab, denn es wird verlangt, dass die partielle Isometrie obiger Definition ebenfalls in A liegt. In einer kommutativen von-Neumann-Algebra
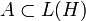 sind äquivalente Projektionen gleich (denn aus e = u * u und f = uu * folgt wegen der Kommutativität e = f), in der größeren von-Neumann-Algebra L(H) ist das nicht der Fall.
sind äquivalente Projektionen gleich (denn aus e = u * u und f = uu * folgt wegen der Kommutativität e = f), in der größeren von-Neumann-Algebra L(H) ist das nicht der Fall.Man kann zeigen, dass
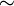 eine Äquivalenzrelation ist und
eine Äquivalenzrelation ist und 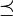 eine partielle Ordnung auf der Menge der Äquivalenzklassen induziert. Insbesondere gilt also
eine partielle Ordnung auf der Menge der Äquivalenzklassen induziert. Insbesondere gilt also 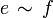 , falls
, falls 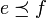 und
und 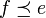 , was der schwierigere Teil des Beweises ist.
, was der schwierigere Teil des Beweises ist.Projektionen in von-Neumann-Algebren
Projektionen in einer von-Neumann-Algebra können eine Reihe von Eigenschaften haben:
- Eine Projektion heißt zentral, wenn sie im Zentrum
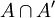 von A liegt. Hier bezeichnet A' die Kommutante von A.
von A liegt. Hier bezeichnet A' die Kommutante von A. - Eine von 0 verschiedene Projektion
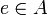 heißt minimal, wenn für jede Projektion
heißt minimal, wenn für jede Projektion 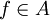 mit
mit 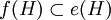 entweder f = 0 oder f = e gilt.
entweder f = 0 oder f = e gilt. - Eine Projektion
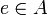 heißt endlich, wenn für jede Projektion
heißt endlich, wenn für jede Projektion 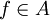 mit
mit 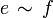 und
und 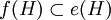 bereits
bereits 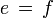 folgt. Man beachte die Analogie zur Mengenlehre: Eine Menge ist genau dann endlich, wenn sie nicht zu einer echten Teilmenge gleichmächtig ist. Minimale Projektionen sind endlich und diese entsprechen in der Analogie zur Mengenlehre den einelementigen Mengen.
folgt. Man beachte die Analogie zur Mengenlehre: Eine Menge ist genau dann endlich, wenn sie nicht zu einer echten Teilmenge gleichmächtig ist. Minimale Projektionen sind endlich und diese entsprechen in der Analogie zur Mengenlehre den einelementigen Mengen. - Nicht-endliche Projektionen heißen unendlich. Eine Projektion
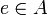 heißt echt unendlich, wenn für jede zentrale Projektion
heißt echt unendlich, wenn für jede zentrale Projektion 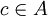 entweder ce = 0 oder ce unendlich ist.
entweder ce = 0 oder ce unendlich ist. - Eine Projektion
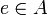 heißt rein unendlich, wenn für jede endliche Projektion
heißt rein unendlich, wenn für jede endliche Projektion 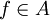 mit
mit 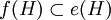 bereits f = 0 folgt. Rein unendliche Projektionen sind echt unendlich.
bereits f = 0 folgt. Rein unendliche Projektionen sind echt unendlich. - Eine Projektion
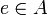 heißt abelsch, falls eAe eine abelsche von-Neumann-Algebra auf e(H) ist. Dazu beachte man, dass mit eAe üblicher Weise die Algebra aller Operatoren
heißt abelsch, falls eAe eine abelsche von-Neumann-Algebra auf e(H) ist. Dazu beachte man, dass mit eAe üblicher Weise die Algebra aller Operatoren 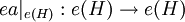 ,
, 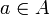 , bezeichnet wird, was stets wieder eine von-Neumann-Algebra ist. Abelsche Projektionen sind endlich.
, bezeichnet wird, was stets wieder eine von-Neumann-Algebra ist. Abelsche Projektionen sind endlich. - Zu jeder Projektion
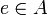 gibt es eine kleinste zentrale Projektion
gibt es eine kleinste zentrale Projektion 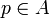 mit e = ep, das heißt für jede andere zentrale Projektion
mit e = ep, das heißt für jede andere zentrale Projektion 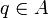 mit e = eq gilt
mit e = eq gilt 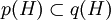 . Diese Projektion p heißt zentraler Träger von e und wird mit Ce bezeichnet.
. Diese Projektion p heißt zentraler Träger von e und wird mit Ce bezeichnet.
Entsprechend heißt eine von-Neumann-Algebra endlich, unendlich, echt unendlich, bzw. rein unendlich, wenn diese Eigenschaften auf das Einselement
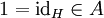 zutreffen. Dieselbe Beziehung gilt offenbar für die Eigenschaft abelsch, das heißt eine von-Neumann-Algebra ist genau dann abelsch (das heißt kommutativ), wenn
zutreffen. Dieselbe Beziehung gilt offenbar für die Eigenschaft abelsch, das heißt eine von-Neumann-Algebra ist genau dann abelsch (das heißt kommutativ), wenn 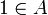 eine abelsche Projektion ist.
eine abelsche Projektion ist.Vergleichbarkeitssatz
Zwei beliebige Projektionen müssen nicht vergleichbar sein. Man kann die von-Neumann-Algebra aber in eine direkte Summe von drei von-Neumann-Algebren zerlegen, so dass in jedem Summanden Vergleichbarkeit vorliegt. Es gilt der folgende Satz:
Vergleichbarkeitssatz: Es seien
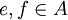 Projektionen in der von-Neumann-Algebra A. Dann gibt es eindeutig bestimmte, paarweise orthogonale, zentrale Projektionen
Projektionen in der von-Neumann-Algebra A. Dann gibt es eindeutig bestimmte, paarweise orthogonale, zentrale Projektionen 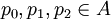 mit p0 + p1 + p2 = 1, so dass folgendes gilt:
mit p0 + p1 + p2 = 1, so dass folgendes gilt: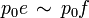 .
.- Ist
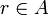 eine zentrale Projektion mit
eine zentrale Projektion mit 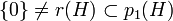 , so gilt
, so gilt 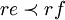 .
. - Ist
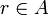 eine zentrale Projektion mit
eine zentrale Projektion mit 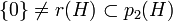 , so gilt
, so gilt 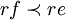 .
.
Dabei steht
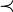 abkürzend für "
abkürzend für "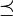 , und
, und 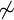 " und zwei Projektionen heißen orthogonal (zueinander), wenn ihr Produkt 0 ist.
" und zwei Projektionen heißen orthogonal (zueinander), wenn ihr Produkt 0 ist.Typ I, Typ II, Typ III
- Eine von-Neumann-Algebra A heißt vom Typ I (lies: Typ eins), wenn es eine abelsche Projektion
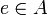 mit Ce = 1 gibt.
mit Ce = 1 gibt. - A heißt genauer vom Typ In, wobei
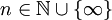 , falls A vom Typ I ist und
, falls A vom Typ I ist und 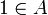 die Summe von n paarweise äquivalenten abelschen Projektionen ist.
die Summe von n paarweise äquivalenten abelschen Projektionen ist. - Eine von-Neumann-Algebra
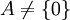 heißt vom Typ II, wenn sie keine von 0 verschiedenen abelschen Projektionen besitzt, aber eine endliche Projektion
heißt vom Typ II, wenn sie keine von 0 verschiedenen abelschen Projektionen besitzt, aber eine endliche Projektion 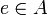 mit Ce = 1.
mit Ce = 1. - Eine von Neumann-Algebra A vom Typ II heißt vom Typ II1, wenn
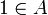 eine endliche Projektion ist.
eine endliche Projektion ist. - Eine von-Neumann-Algebra A vom Typ II heißt vom Typ II∞, wenn
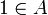 eine echt unendliche Projektion ist.
eine echt unendliche Projektion ist. - Eine von-Neumann-Algebra
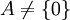 heißt vom Typ III, wenn sie keine von 0 verschiedenen endlichen Projektionen besitzt.
heißt vom Typ III, wenn sie keine von 0 verschiedenen endlichen Projektionen besitzt.
Die Bedingungen für obige Typ-Einteilung sind so angelegt, dass eine von-Neumann-Algebra höchstens von einem Typ sein kann, es gibt aber von-Neumann-Algebren, die von keinem Typ im obigen Sinne sind. Der folgende Satz zeigt, dass man jede von-Neumann-Algebra eindeutig in eine direkte Summe zerlegen kann, so dass alle Summanden einen Typ haben:
Satz von der Typzerlegung: Sei A eine von-Neumann-Algebra. Dann gibt es eindeutig bestimmte, paarweise orthogonale, zentrale Projektionen
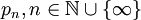 ,
, 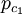 ,
, 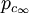 und
und 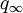 mit Summe 1, so dass gilt:
mit Summe 1, so dass gilt: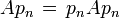 ist vom Typ In oder 0.
ist vom Typ In oder 0.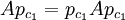 ist vom Typ II1 oder 0.
ist vom Typ II1 oder 0.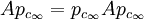 ist vom Typ II∞ oder 0.
ist vom Typ II∞ oder 0.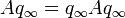 ist vom Typ III oder 0.
ist vom Typ III oder 0.
Es ist
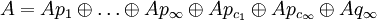 eine direkte Summe von von-Neumann-Algebren.
eine direkte Summe von von-Neumann-Algebren.Viele dieser Projektionen können natürlich 0 sein, A hat dann keinen entsprechenden Typ-Anteil.
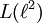 ist eine von-Neumann-Algebra vom Typ I∞. Von-Neumann-Algebren A vom Typ I werden manchmal diskret genannt, da sie eine direkte Summe
ist eine von-Neumann-Algebra vom Typ I∞. Von-Neumann-Algebren A vom Typ I werden manchmal diskret genannt, da sie eine direkte Summe 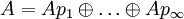 sind; der Summationsindex durchläuft dabei eine diskrete Menge. Beispiele für von-Neumann-Algebren vom Typ II oder III sind aufwändiger, sie können unter anderem durch geeignete Gruppenkonstruktionen gewonnen werden.
sind; der Summationsindex durchläuft dabei eine diskrete Menge. Beispiele für von-Neumann-Algebren vom Typ II oder III sind aufwändiger, sie können unter anderem durch geeignete Gruppenkonstruktionen gewonnen werden.Von-Neumann-Algebren vom Typ II heißen auch stetig. Daher wurden in obigem Satz die Bezeichnungen
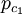 und
und 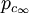 gewählt (c steht für continuous). Bei manchen Autoren gelten auch Typ III Algebren als stetig. Typ III Algebren sind rein unendlich.
gewählt (c steht für continuous). Bei manchen Autoren gelten auch Typ III Algebren als stetig. Typ III Algebren sind rein unendlich.Eine von-Neumann-Algebra ohne Typ III Anteil (das heißt
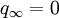 in obigem Satz) heißt semiendlich.
in obigem Satz) heißt semiendlich.Faktoren, Dimensionsfunktion
Da ein Faktor außer 0 und 1 keine weiteren zentralen Projektionen enthält, hat ein Faktor immer genau einen wohlbestimmten Typ. Typ III Faktoren lassen sich weiter klassifizieren; zu jedem
![\lambda\in [0,1]](/pictures/dewiki/97/ada29722c713d4d8a571d9a4ce353ae6.png) kann man nach der auf Alain Connes zurückgehenden Connes-Klassifikation Typ IIIλ Faktoren definieren, auf die hier nicht weiter eingegangen wird. Zu jedem Typ gibt es Faktoren, sogar auf separablen Hilberträumen.
kann man nach der auf Alain Connes zurückgehenden Connes-Klassifikation Typ IIIλ Faktoren definieren, auf die hier nicht weiter eingegangen wird. Zu jedem Typ gibt es Faktoren, sogar auf separablen Hilberträumen.Aus dem Vergleichbarkeitssatz folgt sofort, dass in einem Faktor je zwei Projektionen bzgl.
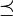 vergleichbar sind. Die minimalen Projektionen fallen mit den abelschen Projektionen zusammen. Betrachtet man nur Faktoren A auf separablen Hilberträumen und ist
vergleichbar sind. Die minimalen Projektionen fallen mit den abelschen Projektionen zusammen. Betrachtet man nur Faktoren A auf separablen Hilberträumen und ist 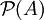 die Menge der Projektionen in A, so kann man die Typen über die Ordnungsstruktur von
die Menge der Projektionen in A, so kann man die Typen über die Ordnungsstruktur von 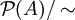 beschreiben. Es gilt folgender Satz:
beschreiben. Es gilt folgender Satz:Satz (Dimensionsfunktion): Ist A ein Faktor auf einem separablen Hilbertraum, so gibt es eine Funktion
![D:{\mathcal P}(A) \rightarrow [0,\infty]](/pictures/dewiki/57/933e1f7270e56fa5fdee05d235617402.png) mit folgenden Eigenschaften:
mit folgenden Eigenschaften:- Für
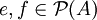 gilt
gilt 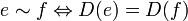
- Für
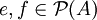 gilt
gilt 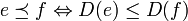
- Für zwei zueinander orthogonale Projektionen
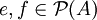 gilt
gilt 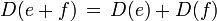 .
. - Für
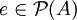 gilt: e endlich
gilt: e endlich 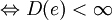 .
.
Die Funktion D ist bis auf einen konstanten Faktor eindeutig bestimmt und heißt Dimensionsfunktion. Das Bild
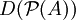 ist bis auf einen Skalierungsfaktor eine der folgenden Mengen:
ist bis auf einen Skalierungsfaktor eine der folgenden Mengen: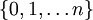 für ein
für ein 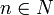 ; A ist dann vom Typ In.
; A ist dann vom Typ In.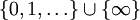 ; A ist dann vom Typ I∞.
; A ist dann vom Typ I∞.![[0,\,1]](/pictures/dewiki/51/3c677f273d5640cb290c4e4ac717fbc7.png) ; A ist dann vom Typ II1.
; A ist dann vom Typ II1.![[0,\infty]](/pictures/dewiki/51/315e0047ccbfa87354192dac2fe986fb.png) ; A ist dann vom Typ II∞.
; A ist dann vom Typ II∞.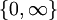 ; A ist dann vom Typ III.
; A ist dann vom Typ III.
Für den Typ I∞ Faktor
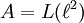 erhält man bei der angegebenen Skalierung
erhält man bei der angegebenen Skalierung 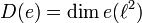 für alle
für alle 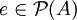 . Das erklärt den Namen Dimensionsfunktion.
. Das erklärt den Namen Dimensionsfunktion.Man beachte, dass D eine ordnungstreue Bijektion
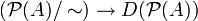 induziert. Der Typ eines Faktors ist daher nach obigem Satz durch die Ordnungsstruktur von
induziert. Der Typ eines Faktors ist daher nach obigem Satz durch die Ordnungsstruktur von 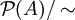 festgelegt.
festgelegt.Quellen
- R.V. Kadison, J. R. Ringrose: Fundamentals of the Theory of Operator Algebras II, Academic Press Inc. 1986
- V. S. Sunder: An Invitation to Von Neumann Algebras (1987), ISBN 0387963561
- Eine Projektion heißt zentral, wenn sie im Zentrum
Wikimedia Foundation.
