Shannons Entwicklungssatz

Der Entwicklungssatz von Claude Shannon ist ein Satz über Boolesche Funktionen, der die Shannon-Zerlegung verwendet. Er lautet wie folgt:

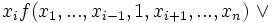
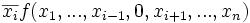
y = f(x1,...,xi,...,xn)	=	$x_{i}f(x_1,...,x_{i-1},1,x_{i+1},...,x_n)\ \vee$
		$\overline {x_i}f(x_1,...,x_{i-1},0,x_{i+1},...,x_n)$

Diese Formel sieht zunächst etwas kompliziert aus. Die Aussage betrifft eine n-stellige Boolesche Funktion f und dabei insbesondere deren Parameter x_i. Man sagt auch, die Funktion f wird durch Anwendung des Satzes "nach x_i entwickelt". Wiederholt man die Anwendung des Satzes für eine beliebige Funktion f auf alle ihre n Parameter, so gelangt man zu einer Darstellung der Funktion, welche ausschließlich die Operatoren ∧, ∨ und ¬ verwendet.

Mit anderen Worten: Die rekursive Anwendung des Entwicklungssatzes von Shannon liefert einen Beweis, dass sich ausnahmslos jede Boolesche Funktion mittels der Operatoren ∧, ∨ und ¬ ausdrücken lässt. Darüber hinaus kann der Entwicklungssatz etwa zur Herleitung klammerfreier Ausdrücke verwendet werden.

Beispiel

Gegeben sei die Boolesche Funktion $y = f(x_{1},x_{2},x_{3}) = x_{1}x_{2}\overline {x_{3}} \vee \overline {x_{1}}x_{2} \vee \overline {x_{2}}x_{3}$.

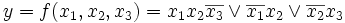Diese soll zunächst nach x₁, dann nach x₂ und schließlich nach x₃ entwickelt werden:

y	$= x_{1}[x_{2}\overline {x_{3}} \vee \overline {x_{2}}x_{3}] \vee \overline {x_{1}}[x_{2} \vee \overline {x_{2}}x_{3}]$ (Entwicklung nach x1)
	$= x_{1}[x_{2}(\overline {x_{3}}) \vee \overline {x_{2}}(x_{3})] \vee \overline {x_{1}}[x_{2}(1) \vee \overline {x_{2}}(x_{3})]$ (Entwicklung nach x2)
	$= x_{1}[x_{2}(\overline {x_{3}}) \vee \overline {x_{2}}(x_{3})] \vee \overline {x_{1}}[x_{2}(x_{3} \vee \overline {x_{3}}) \vee \overline {x_{2}}(x_{3})]$ (Entwicklung nach x3)
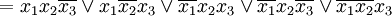	$= x_{1}x_{2}\overline {x_{3}} \vee x_{1}\overline {x_{2}}x_{3} \vee \overline{x_{1}}x_{2}x_{3} \vee \overline {x_{1}}x_{2}\overline {x_{3}} \vee \overline {x_{1}}\overline{x_{2}}x_{3}\$ (Anwendung des Distributivgesetzes)

Siehe auch

• Shannon-Zerlegung