Shift-Operator

Shiftoperatoren werden im mathematischen Teilgebiet der Funktionalanalysis betrachtet. Beim unilateralen Shiftoperator (s.u.) handelt es sich um einen konkreten nicht-normalen Operator auf einem Hilbertraum. Dieser Operator hat viele Eigenschaften, zu denen es keine endlich-dimensionale Entsprechung gibt.

Definition

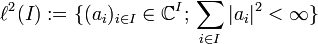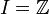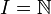Ein unendlich-dimensionaler separabler Hilbertraum ist nach dem Satz von Fischer-Riesz isometrisch isomorph zu $\ell^2(I) := \{(a_i)_{i\in I} \in {\mathbb C}^I; \,\sum_{i\in I}|a_i|^2 < \infty\}$, wobei I eine abzählbar unendliche Menge ist, z.B. $I={\mathbb Z}$ oder $I={\mathbb N}$. Der Operator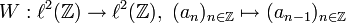

$W:\ell^2({\mathbb Z}) \rightarrow \ell^2({\mathbb Z}), \,\, (a_n)_{n\in{\mathbb Z}} \mapsto (a_{n-1})_{n\in{\mathbb Z}}$

heißt bilateraler Shiftoperator.

$S:\ell^2({\mathbb N}) \rightarrow \ell^2({\mathbb N}), \,\, (a_n)_{n\in{\mathbb N}} \mapsto (0,a_1,a_2,\ldots)$

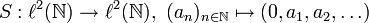
heißt unilateraler Shiftoperator. Die Bezeichnung Shiftoperator rührt daher, dass diese Operatoren die Folgenglieder um eine Indexposition verschieben. Beim bilateralen Shiftoperator sind Indizes auf beiden Seiten der Null betroffen, positive wie negative, beim unilateralen Shiftoperator nur die Indizes einer Seite, nämlich nur die positiven. In der mathematischen Literatur steht Shiftoperator, ohne weiteren Zusatz, in der Regel für den unilateralen Shiftoperator. Oft lässt man auch den Wortbestandteil Operator fort und spricht einfach vom Shift.

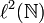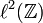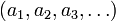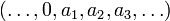Fasst man $\ell^2({\mathbb N})$ als Unterraum von $\ell^2({\mathbb Z})$ auf, indem man $(a_1,a_2,a_3,\ldots)$ mit $(\ldots,0,a_1,a_2,a_3,\ldots)$ identifiziert, so sieht man, dass 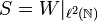$S=W|_{\ell^2({\mathbb N})}$ ist, das heißt der unilaterale Shiftoperator ist eine Einschränkung des bilateralen Shiftoperators.

Der bilaterale Shift

Der bilaterale Shift W ist ein unitärer Operator, die Umkehrung ist der adjungierte Operator

$W^*:\ell^2({\mathbb Z}) \rightarrow \ell^2({\mathbb Z}), \,\, (a_n)_{n\in{\mathbb Z}} \mapsto (a_{n+1})_{n\in{\mathbb Z}}$.

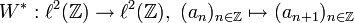Das Spektrum des bilateralen Shifts ist die gesamte Kreislinie, das heißt 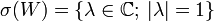$\sigma(W) = \{\lambda\in{\mathbb C};\,|\lambda|=1\}$. Kein Element des Spektrums ist ein Eigenwert.

Der unilaterale Shift

Der unilaterale Shift S ist eine Isometrie, die nicht surjektiv ist, denn das Bild ist die Menge alle Folgen aus 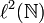$\ell^2({\mathbb N})$, deren erste Komponente 0 ist. Damit ist S ein injektiver linearer Operator, der nicht surjektiv ist; dies ist ein Phänomen, das aus der Theorie der endlich-dimensionalen Räume, das heißt in der linearen Algebra, nicht vorkommt.

Der adjungierte Operator ist

$S^*:\ell^2({\mathbb N}) \rightarrow \ell^2({\mathbb N}), \,\, (a_n)_{n\in{\mathbb N}} \mapsto (a_2,a_3,\ldots)$.

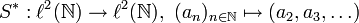Damit folgt sofort S * S = id und SS * = P_im(S), wobei letzteres für die Orthogonalprojektion auf das Bild von S steht. Insbesondere ist S nicht normal. Man kann sogar zeigen, dass der Shiftoperator von jedem unitären Operator genau den maximal möglichen Normabstand 2 hat.

Das Spektum des Shiftoperators

Das Spektrum von S ist die volle Kreisscheibe: 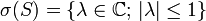$\sigma(S)= \{\lambda\in{\mathbb C};\,|\lambda|\le 1\}$. Keiner der Spektralpunkte ist ein Eigenwert. Die Spektralpunkte λ mit | λ | = 1 sind aber sogenannte approximative Eigenwerte, das heißt es gibt eine Folge (x_n)_n von Vektoren mit Norm 1, so dass 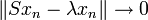$\|Sx_n-\lambda x_n\|\to 0$. Für die inneren Spektralpunkte λ mit | λ | < 1 gilt das nicht.

Das Spektrum des adjungierten Operators S ^* ist ebenfalls die volle Kreisscheibe und der Kreisrand besteht ebenfalls aus lauter approximativen Eigenwerten, die keine echten Eigenwerte sind. Die inneren Spektralpunkte λ mit | λ | < 1 sind sämtlich Eigenwerte von S ^* . Die zugehörigen Eigenräume sind alle eindimensional, der Eigenraum zu λ wird von 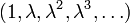$(1,\lambda,\lambda^2,\lambda^3,\ldots)$ erzeugt.

Der Shiftoperator als Fredholm-Operator

Der Shiftoperator S ist ein Fredholm-Operator mit ind(S) = dim(ker(S)) − codim(im(S)) = − 1. Daher ist das Bild π(S) in der Calkin-Algebra unitär, was man aber auch ohne den Begriff des Fredholm-Operators den Formeln S * S = id und SS * = P_im(S) entnimmt. Das Spektrum von π(S) ist die Kreislinie.

Wold-Zerlegung

Ein stetiger linearer Operator T auf einem Hilbertraum H ist unitär äquivalent zum Shiftoperator, wenn es einen unitären Operator 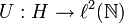$U:H\rightarrow \ell^2({\mathbb N})$ gibt mit T = U ^* SU. Ist T irgendein Operator auf H, so heißt ein Unterraum 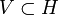$V\subset H$ invariant (bzgl. T), falls 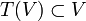$T(V)\subset V$. Mit diesen Begriffen kann man nun alle Isometrien auf einem Hilbertraum beschreiben. Eine Isometrie ist im Wesentlichen eine direkte Summe aus einem unitären Operator und einigen Shiftoperatoren, genauer:

• Ist T eine Isometrie auf einem Hilbertraum H, so zerfällt H in eine direkte Summe 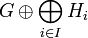$G \oplus \bigoplus_{i\in I}H_i$ invarianter Unterräume, so dass T | _G unitär ist und jeder Operator 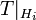$T|_{H_i}$ unitär äquivalent zum Shiftoperator ist.

Dabei kann G = {0} sein, das heißt der unitäre Anteil der Isometrie verschwindet, aber auch G = H und somit 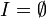$I=\emptyset$, dann ist die Isometrie unitär. Diese Darstellung einer Isometrie nennt man auch ihre Wold-Zerlegung oder Wold-von Neumann-Zerlegung (nach Herman Wold und John von Neumann).

Der Shiftoperator auf H²

Sei 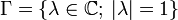$\Gamma = \{\lambda \in {\mathbb C};\,|\lambda|=1\}$ die Kreislinie und μ das auf 1 normierte Lebesgue-Maß auf Γ, das heißt das Bildmaß des Lebesgue-Maßes auf dem Einheitsintervall [0,1] unter der Abbildung 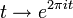$t\to e^{2\pi it}$. H², der sogenannte Hardy-Raum, ist definiert als der von den Funktionen 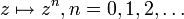$z\mapsto z^n, n=0,1,2,\ldots$ erzeugte Unterraum im Hilbertraum L²(Γ,μ).

Man kann zeigen, dass die Multiplikation mit der Funktion 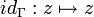$id_\Gamma:z\mapsto z$ einen stetigen, linearen Operator auf H² definiert. Da die Funktionen 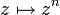$z\mapsto z^n$ eine Orthogonalbasis des Hardy-Raums bilden, ist dieser Operator unitär äquivalent zum Shiftoperator, und man bezeichnet ihn auch einfach als Shiftoperator. In dieser speziellen Darstellung des Shiftoperators erscheint der Shiftoperator als ein Multiplikationsoperator.

Quellen

Paul Halmos: A Hilbert Space Problem Book, Springer-Verlag, ISBN 0387906851