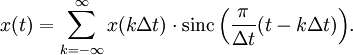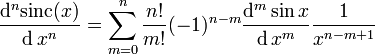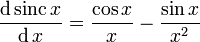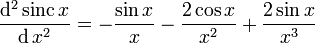- Si-Funktion
-
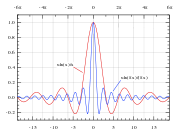
Der Sinus cardinalis, auch sinc-Funktion, Kardinalsinus oder Spaltfunktion ist eine mathematische Funktion welche nicht normiert als
definiert wird. In der Informationstheorie und der digitalen Signalverarbeitung, einen wichtigen Anwendungsgebiet der sinc-Funktion, findet hingegen meist die normierte Form:
Anwendung. Neben sinc ist insbesondere in deutschsprachiger Fachliteratur auch die Abkürzung si gebräuchlich, welche nicht mit dem Integralsinus Si(x), der Stammfunktion der sinc-Funktion, zu verwechseln ist.
Inhaltsverzeichnis
Allgemeines
An der hebbaren Singularität bei x=0 wird die Funktion durch den Grenzwert sinc(0)=1 fortgesetzt, der sich aus der Regel von L'Hospital ergibt; manchmal wird die Definitionsgleichung auch mit Fallunterscheidung geschrieben.
Softwarepakete wie Matlab verwenden die normierte sinc-Funktion welche sich auch als Produkt oder mit Hilfe der Gammafunktion Γ ausdrücken lässt als:
Die Taylorreihe der sinc-Funktion lässt sich unmittelbar aus der sin-Funktion ableiten zu:
Darstellung als Fouriertransformierte der Rechteckfunktion
Die sinc-Funktion ist die Fouriertransformierte der Rechteckfunktion
denn es gilt
![\mathcal F(\chi_{[-\tau/2,\tau/2]})(\omega)
= \frac1{\sqrt{2\pi}}\int \limits_{-\tau/2}^{\tau/2} e^{-\mathrm{i} \omega t}\, \mathrm dt
= \frac1{\sqrt{2\pi}}\,\tau \,\mathrm{sinc} \left( \frac{\omega \tau}{2} \right)](/pictures/dewiki/57/98813e69a5ff8e6044ef9916eebc35e2.png) .
.
Aus den Eigenschaften der Fourier-Transformation folgt, dass die sinc-Funktion analytisch und damit beliebig oft stetig differenzierbar ist. Aus der Plancherel-Identität der Fourier-Transformation folgt weiter, dass sie orthogonal zu Verschiebungen ihrer selbst um ganzzahlige Vielfache von π ist, es gilt
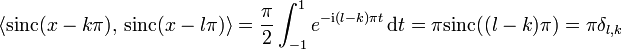 ,
,
wobei δl,k das Kronecker-Delta bezeichnet.
Mit einer passenden Normierung bilden diese Verschiebungen der sinc-Funktion also ein Orthonormalsystem im Funktionenraum
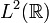 . Die Projektion auf den von den sinc(x - kπ) aufgespannten Unterraum ergibt sich als
. Die Projektion auf den von den sinc(x - kπ) aufgespannten Unterraum ergibt sich als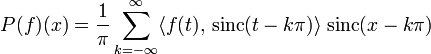 .
.
Aufgrund der Interpolationseigenschaft gilt
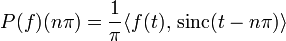 , also
, also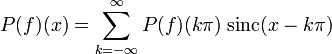 .
.
Funktionen aus diesem Unterraum sind also durch ihre Werte an den Stellen
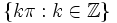 eindeutig bestimmt.
eindeutig bestimmt.Die Rechteckfunktion als Fouriertransformierte der sinc-Funktion hat beschränkten Träger, ist daher samt der Linearkombinationen ihrer Verschiebungen bandbeschränkt. Umgekehrt ist jede bandbeschränkte als eine solche Linearkombination darstellbar, und daher durch die Funktionswerte an den genannten Stützstellen eindeutig bestimmt. Das ist die Aussage des WKS-Abtasttheorems.
Aufbaufunktion zur Signalrekonstruktion
Die sinc-Funktion hat insbesondere in der Signalverarbeitung eine große Bedeutung. Sie tritt in der sogenannten Samplingreihe (oder Kardinalreihe, E. T. Whittaker 1915) auf, mit Hilfe derer ein kontinuierliches bandbeschränktes Signal x aus seinen Abtastwerten x(kΔt) rekonstruiert bzw. eine beliebige Stützstellenfolge zu einem kontinuierlichen Signal fortgesetzt wird:
Diese ist die Interpolationsformel geringster Schwankung, d. h. das Frequenzspektrum ist beschränkt und hat die kleinstmögliche höchste (Kreis-)Frequenz
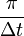 bzw. Frequenz
bzw. Frequenz 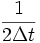 . Hat das Ausgangssignal Anteile höherer Frequenzen, so ist die Folge dieser Abtastwerte zu grobmaschig, die hochfrequenten Anteile werden in zusätzliche niederfrequente Anteile umgesetzt, d. h. es tritt Aliasing (Fehlzuordnung der Frequenzanteile) auf.
. Hat das Ausgangssignal Anteile höherer Frequenzen, so ist die Folge dieser Abtastwerte zu grobmaschig, die hochfrequenten Anteile werden in zusätzliche niederfrequente Anteile umgesetzt, d. h. es tritt Aliasing (Fehlzuordnung der Frequenzanteile) auf.Beugung am Spalt
Bei der Beugung von Wellen an einem Spalt bilden die Amplituden ein Beugungsmuster, das sich durch Fouriertransformation einer rechteckigen Öffnungsfunktion erklären lässt. Deshalb wird der Kardinalsinus auch als Spaltfunktion bezeichnet. Die bei der Beugung von Licht vom Auge wahrgenommene Helligkeitsverteilung ist allerdings das Quadrat der Wellenamplitude; sie folgt daher der quadrierten Funktion
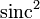 .
.Ableitungen
Die n-te Ableitung von
lässt sich für alle x ≠ 0 analytisch bestimmen zu:
Die daraus gebildeten ersten zwei Ableitungen lauten:
Nullstellen
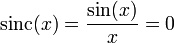 gilt für
gilt für 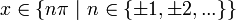
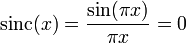 gilt für
gilt für 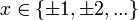
Maxima
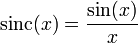 hat Maxima bei
hat Maxima bei 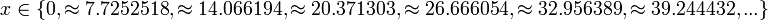
Minima
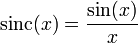 hat Minima bei
hat Minima bei 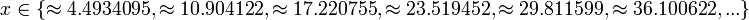
Siehe auch
Weblinks
Wikimedia Foundation.

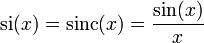
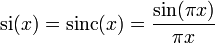
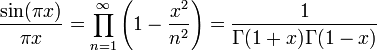
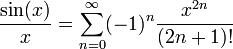
![\mathrm{rect} \left(\frac{t}{\tau} \right) =\chi_{[-\tau/2,\tau/2]}(t)
:= \begin{cases}1 & |t|\le\tau/2 \\ 0 & \mathrm{sonst} \end{cases}](/pictures/dewiki/98/b5ad14b2877511916563aa757c26e8ed.png)