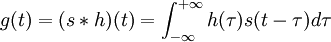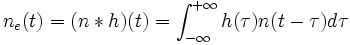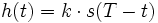Signalangepasstes Filter

Unter Optimalfilter (engl. matched filter) versteht man in der Nachrichtentechnik ein Filter, das das Signal-Rausch-Verhältnis (engl. signal to noise ratio, SNR) optimiert. In der Literatur findet man auch häufig die Bezeichnungen Signal-angepasstes Filter oder nur angepasstes Filter. Das Optimalfilter dient zur optimalen Bestimmung des Vorhandenseins (Detektion) der Amplitude oder der Lage einer bekannten Signalform in Gegenwart von weißem Rauschen (Parameterschätzung).

Problem und Aufgabenstellung

In Signalübertragungssystemen tritt immer das Problem auf, dass das zu empfangende Nutzsignal (z. B. das einzelne Datenbit einer Folge, das Echosignal eines Radarsenders) von einem mehr oder weniger großem Störsignal überlagert wird. Dadurch wird die Erkennung des Nutzsignals im Empfänger erschwert. Im „normalen“ (sog. Leistungs-)Empfänger wird das Unter- oder Überschreiten einer Amplitudenschwelle des empfangenen Signal-Rauschgemischs als „kein Signal“ oder „Signal vorhanden“ gewertet. Ist das Signal schwach, besteht immer die Gefahr, dass einzelne Nutzsignale nicht erkannt oder Störsignalspitzen fälschlich als Nutzsignale interpretiert werden.

Es stellt sich deshalb die grundsätzliche Frage nach der Dimensionierung einer optimalen Filterstruktur des Empfängers, die ein Nutzsignal im Rauschen maximal sicher erkennt, die Fehlerwahrscheinlichkeit also minimiert.

Die Abbildung zeigt ein nachrichtentechnisches System zur Übertragung einer digitalen Sendedatenfolge welche links im Bild über den AWGN Channel übertragen werden soll. Der AWGN Channel stellt abstrakt einen mit weißem Rauschen gestörten Übertragungskanal dar, beispielsweise eine stark gestörte Funkstrecke. Am Empfänger kommt dann das vor dem Matched-Filter dargestellte stark mit Rauschen überlagerte Empfangsignal an. Darin ist die ursprüngliche Sendesignalfolge nicht mehr erkennbar, es käme bei direkter Auswertung dieses Signals zu massiven Fehlern.

Das stark gestörte Empfangssignal wird daher dem Matched-Filter zugeführt, welcher in seiner Impulsantwort optimal an die links dargestellte Sendeimpulseform angepasst ist. Durch diese Anpassung ist es möglich, dass am Ausgang des Filters ein Signal gewonnen werden kann, welches schon der ursprünglichen Sendesignalfolge etwas besser entspricht. Durch eine dem Filter rechts außen nachgeschaltene Abtaststufe und Requantisierung kann daraus eindeutig und mit minimaler Bitfehlerwahrscheinlichkeit die ursprüngliche Bitfolge des Senders am Empfänger rekonstruiert werden.

Mathematische Grundlagen

Die folgenden Betrachtungen gehen davon aus, dass die Struktur des ausgesendeten Signals beim Empfänger bekannt ist. Es ist dabei wichtig, dass diese Annahme nicht bedeutet, dass die übermittelte Nachricht bekannt ist – die Kenntnis der Zeitfunktion eines Datenbits sagt ja noch nichts aus über die in einer Bitfolge übermittelten Information!

Das zu erwartende zeitlich begrenzte Nutzsignal (in dem genannten Sinne etwa eines einzelnen Bits oder des Echosignals eines Radarsystems) sei s. Es sei überlagert von einem weißen Rauschsignal n mit einer spektralen Leistungsdichte N₀. Die gesuchte optimale Filterstruktur sei durch ihre Antwortfunktion h auf einen Dirac-Impuls gekennzeichnet. Das Ausgangssignal eines solchen Filters zum Zeitpunkt t ist dann

(1) $\!\,y(t)=([s+n]*h)(t)=(s*h)(t)+(n*h)(t)=g(t)+n_e(t)$,

wobei g die Antwort des Filters auf das Nutzsignal s und n_e die Antwort des Filters auf das Störsignal n darstellen, die jeweils durch die Faltungsoperation mit der Impulsantwort h des Filters entstehen:

$g(t)=(s*h)(t)=\int_{-\infty}^{+\infty}h(\tau)s(t-\tau)d\tau$

$n_e(t)=(n*h)(t)=\int_{-\infty}^{+\infty}h(\tau)n(t-\tau)d\tau$

Der erste Term g(t) in (1) beschreibt offenbar den Nutzsignalanteil zum Zeitpunkt t, der zweite Term n_e(t) den Störsignalanteil zum Zeitpunkt t. Als Kriterium für die Sicherheit der Nutzsignalerkennung sei das Verhältnis der Momentanleistungen von Nutz- und Störsignalanteil zu einer Zeit T vorausgesetzt; zu diesem Zeitpunkt soll das Filterausgangssignal abgetastet und die Entscheidung über ein etwa vorhandenes Nutzsignal getroffen werden. Je größer der Nutzsignalanteil gegenüber dem Störsignalanteil am Filterausgang ist, desto größer wird offenbar die Erkennungswahrscheinlichkeit sein.

Die Leistung des Nutzsignalanteils zum Zeitpunkt T ist S = g²(T). Für die Störleistung gilt mit dem Parsevalschen Theorem

(2) $N=N_0\int_{-\infty}^{+\infty} h^2(t)dt$

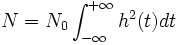
Das Verhältnis S / N wird also

(3) $\frac{S}{N}= \frac{[\int_{-\infty}^{+\infty}h(\tau)s(T-\tau)d\tau]^2}{N_0\int_{-\infty}^{+\infty}h^2(t)dt}$

Die Energie E des zeitbegrenzten Nutzsignals ist gegen eine Zeitverschiebung invariant; es kann also geschrieben werden

(4) $E=\int_{-\infty}^{+\infty} s^2(t)dt=\int_{-\infty}^{+\infty} s^2(T-\tau)d\tau$

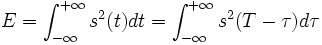
Wird (3) mit (4) erweitert, ergibt sich ein Ausdruck

(5) $\frac{S}{N}=\frac{E}{N_0}\frac{[\int_{-\infty}^{+\infty} h(\tau)s(T-\tau)d\tau]^2}{\int_{-\infty}^{+\infty} h^2(\tau)d\tau \int_{-\infty}^{+\infty} s^2(T-\tau)d\tau}$

Der rechte Teil des Bruchs kann als Quadrat des Korrelationsfaktors ρ zwischen der Antwortfunktion h(t) des gesuchten Filters und der Signalfunktion s(t) interpretiert werden ($-1\leq\rho\leq +1$):

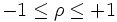(6) $\frac{S}{N}=\frac{E}{N_0}(\rho_{hs})^2$

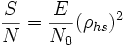
Ergebnis

Das Verhältnis 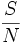$\frac{S}{N}$ (genannt Signal-Rausch-Verhältnis oder Signal-Geräusch-Abstand) wird dann maximal, wenn 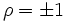$\rho=\pm 1$ ist, wenn also gilt

$h(t)=k\cdot s(T-t)$

(k - beliebige Konstante). Daraus folgt die wesentliche Aussage: Um eine maximale Erkennungssicherheit des Nutzsignals im Rauschen zu erhalten, muss die gesuchte Impulsantwort h(t) des optimalen Filters gleich der zeitgespiegelten („rückwärts laufenden“) Nutzsignalfunktion s(t) sein (angepasstes Filter).

Im rauschfreien Fall würde an dieses Filter als Antwort auf das Nutzsignal der Dauer T dessen Autokorrelationsfunktion erscheinen, und zum Zeitpunkt T (also gerade dann, wenn die gesamte Energie des Signals in das Filter eingelaufen ist) dessen Maximalwert abgetastet werden.

Im Fall der Anwendung des Optimalfilters wird also (im Gegensatz zum oben erwähnten Leistungsempfang!) im Empfänger nicht die Signalform selbst ausgewertet – was ja auch überflüssig ist, da sie als bekannt vorausgesetzt wurde – sondern dessen Autokorrelationsfunktion (deshalb auch die Bezeichnung als Korrelationsfilter).

Diese Tatsache lässt eine weitere Realisierung des Optimalempfangs zu: Im Empfänger kann auch der vollständige Vorgang der Korrelation realisiert werden, d.h. eine Multiplikation des ankommenden Signal-Störgemischs mit der am Ort des Empfängers ja bekannten Nutzsignalfunktion und anschließende Integration und Abtastung. Das empfiehlt sich jedoch nur dann, wenn der Erwartungszeitpunkt des Nutzsignals bekannt ist.

• Eine zweite wesentliche Erkenntnis aus der Optimalfilterbedingung ist die zunächst erstaunliche Tatsache, dass allein die Energie des ankommenden (und damit auch des gesendeten) Nutzsignals den Wert S / N und damit die Erkennungsicherheit bestimmt (allerdings eben nur, wenn auch tatsächlich ein Optimalfilter eingesetzt wird). Zeitverlauf, Frequenzspektrum, Signalbandbreite oder andere Parameter können ohne Verletzung der Optimalbedingung nach Notwendigkeit des Übertragungsystems frei gewählt werden.

Auf Grund dieser Aussage ist es z. B. möglich, anstelle eines immer leistungsbegrenzten schmalen Einzelimpulses in einem Radarsystem einen viel breiteren (und deshalb energiereicheren) strukturierten Sendeimpuls zu verwenden, sofern nur dessen Autokorrelationsfunktion ein einziges schmales Maximum und schnell abklingende Werte jenseits τ = 0 aufweist.

Eine erste Veröffentlichung zur Analyse angepasster Filter, hier bereits angewendet auf Radarsignale, stammt von Dwight O. North 1943. ^[1]

Literatur

• Jens-Rainer Ohm, Hans Dieter Lüke: Signalübertragung: Grundlagen der digitalen und analogen Nachrichtenübertragungssysteme. 10. Auflage. Springer, Berlin 2007, ISBN 3540692568. 

Einzelnachweise

1. ↑ D. O. North: Analysis of the factors which determine signal/noise discrimination in radar. In: Report PPR-6C, RCA Laboratories, Princeton, NJ. 1943. 
   Nachdruck: D. O. North: An Analysis of the factors which determine signal/noise discrimination in pulsed-carrier systems. In: Proceedings of the IEEE. 51, Nr. 7, 1963, S. 1016–1027.