Signalenergie

Definition

Der Begriff Energiesignal kommt aus der Signalverarbeitung, und bezeichnet ein Signal mit endlicher Signalenergie.

Definition für kontinuierliche Signale

Ein komplexwertiges kontinuierliches Signal s heißt genau dann Energiesignal, wenn gilt:

$\int \limits _{-\infty}^{\infty} {s(t) \cdot s^{*}(t) dt} < \infty.$

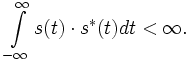
Falls s nur reelle Werte annimmt, vereinfacht sich die Gleichung zu

$\int \limits_{-\infty}^{\infty} {s^2(t) dt} < \infty.$

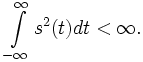
Mit der Beziehung 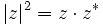$|z|^2 = z \cdot z^{*}$ gilt somit allgemein: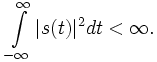

$\int \limits_{-\infty}^{\infty} {|s(t)|^2 dt} < \infty.$

Definition für diskrete Signale

Ein komplexwertiges diskretes Signal s heißt Energiesignal, wenn gilt:

$\sum_{n=-\infty}^{\infty} {s(n) \cdot s^{*}(n)} < \infty$

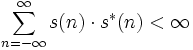
Bei rein reellwertigen diskreten Signalen s gilt entsprechend:

$\sum_{n=-\infty}^{\infty} {s^2(n)} < \infty$

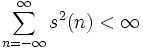
Wie üblich wurde mit s ^* die zu s konjugiert komplexe Zahl bezeichnet. Der Wert des jeweiligen Integrals bzw. der jeweiligen Summe heißt Signalenergie.

Typische Energiesignale

Typische Energiesignale sind alle Signale, die endliche Signalwerte darstellen und irgendwann an- und abgeschaltet werden. Beispielhaft zu nennen sind Ausschwingvorgänge oder einzelne, zeitlich begrenzte Pulse. Typische Nichtenergiesignale sind alle Leistungssignale. Eine besondere Stellung in der Theorie nimmt der Dirac-Impuls ein, der ebenfalls kein Energiesignal ist.

Physikalischer Hintergrund

Die Signalverarbeitung lehnt sich in den Begriffen an der Physik bzw. Elektrotechnik an. Betrachtet man als Signal beispielsweise einen Strom i, der über einen Widerstand R fließt, so berechnet sich die Momentanleistung zu 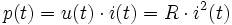$p(t)=u(t)\cdot i(t)=R \cdot i^2(t)$ und entsprechend die insgesamt umgesetzte Energie zu $E=R \cdot \int \limits_{t=-\infty}^{\infty}i^2(t) dt$.

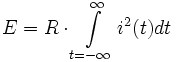Signaltheoretischer Hintergrund

Signaltheoretisch bildet die Menge der Energiesignale zusammen mit der Addition von Funktionen und der Multiplikation mit einer reellen bzw. komplexen Zahl einen Vektorraum mit unendlich vielen Basisvektoren. Als Basisvektoren kommen insbesondere Sinus- und Cosinusfunktionen in Betracht. Die Fouriertransformation ist das wesentliche Element des mit diesen Basisvektoren ausgestatteten Vektor- bzw. Signalraums.

Siehe auch

• Leistungssignal