- Silver-Pohlig-Hellman-Algorithmus
-
Der Pohlig-Hellman-Algorithmus wurde nach den Mathematikern Stephen Pohlig und Martin Hellman benannt. Gelegentlich ist dieser Algorithmus in der Literatur auch unter dem Namen Silver-Pohlig-Hellman-Algorithmus zu finden. Mit dem Pohlig-Hellman-Algorithmus kann der diskrete Logarithmus in einer zyklischen Gruppe berechnet werden.
Die Relevanz dieses Verfahrens liegt darin, dass der Rechenaufwand nicht von der Gruppenordnung, sondern vom größten Faktor der Gruppenordnung abhängt. Nachteilig ist, dass für dieses Verfahren eine Primfaktorzerlegung der Gruppenordnung bekannt sein muss. Solch eine Primfaktorzerlegung ist im allgemeinen jedoch nur sehr schwer zu bestimmen.
Inhaltsverzeichnis
Mathematischer Hintergrund
Sei G eine zyklische Gruppe der Ordnung n, wobei die Faktorisierung von n bekannt und p der größte Faktor von n sei. Der diskrete Logarithmus in der Gruppe G lässt sich dann mittels Silver-Pohlig-Hellman in
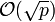 statt
statt 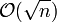 Operationen berechnen. Dies geschieht in drei Schritten:
Operationen berechnen. Dies geschieht in drei Schritten:- Reduktion des Problems von der Gruppe G in zyklische Gruppen
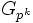 deren Ordnung pk ist, wobei pk ein Teiler von n ist (die sich später hieraus ergebende Lösung ist eindeutig nach dem Chinesischen Restsatz).
deren Ordnung pk ist, wobei pk ein Teiler von n ist (die sich später hieraus ergebende Lösung ist eindeutig nach dem Chinesischen Restsatz). - Reduktion von Gruppen mit Primzahlpotenzordnung in Gruppen mit Primordnung
- Zusammensetzen des Ergebnisses mittels des Chinesischen Restsatzes.
Der Algorithmus
Sei G die zyklische Gruppe der Ordnung n, g ein Generator von G und
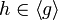 . Weiter sei
. Weiter sei 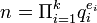 die Primfaktorzerlegung von n.
die Primfaktorzerlegung von n.Der Algorithmus ist nun in zwei Schritten angegeben. Zuerst folgt eine Version für Gruppen, deren Ordnung einer Primzahlpotenz entspricht. Dieser kann im folgenden als Unteralgorithmus im allgemeinen Pohlig-Hellman verwendet werden.
Prime-Power-Pohlig-Hellman
Die Gruppenordnung sei n = qe, wobei q eine Primzahl ist. Zur Bestimmung des diskreten Logarithmus in den Untergruppen wird der Babystep-Giantstep-Algorithmus von Shanks verwendet.
- Eingabe: g,q,e,h
- Ausgabe Der diskrete Logarithmus a: = logg(h)
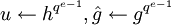
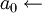 Shanks(
Shanks(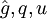 ),
), 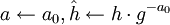
- for
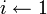 to e-1 do
to e-1 do
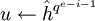
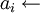 Shanks(
Shanks(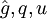 )
)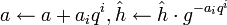
- return a
In diesem Algorithmus wird verwendet, dass der diskrete Logarithmus a = logg(h) in der folgenden Form geschrieben werden kann:
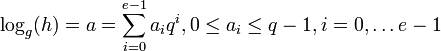 . Aufgrund der vorgenommenen Beschränkungen ist diese Darstellung eindeutig.
. Aufgrund der vorgenommenen Beschränkungen ist diese Darstellung eindeutig.Allgemeiner Pohlig-Hellman
- Eingabe:
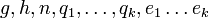
- Ausgabe Der diskrete Logarithmus a: = logg(h)
- for
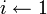 to k do
to k do
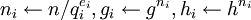
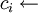 Prime-Power-Pohlig-Hellman(gi,qi,ei,hi)
Prime-Power-Pohlig-Hellman(gi,qi,ei,hi)
- Berechne für
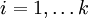 mit dem Chinesischen Restsatz
mit dem Chinesischen Restsatz 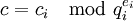 .
. - return c.
- for
Referenzen
- S. Pohlig and M. Hellman. "An Improved Algorithm for Computing Logarithms over GF(p) and its Cryptographic Significance", IEEE Trans. Information Theory 24, 1978, Seiten. 106-110.
- V. Shoup. "A Computational Introduction to Number Theory and Algebra", Cambridge University Press, 2007, http://shoup.net/ntb/, Seite 325ff.
- Reduktion des Problems von der Gruppe G in zyklische Gruppen
Wikimedia Foundation.
