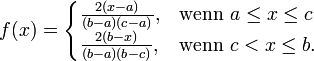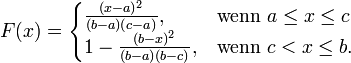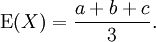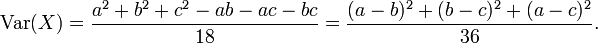Simpsonverteilung

Definition

In der Wahrscheinlichkeitstheorie und Statistik bezeichnet man als Dreiecksverteilung (oder Simpson-Verteilung) eine stetige Wahrscheinlichkeitsverteilung mit der auf dem Intervall $\left[a, b\right]$ definierten Wahrscheinlichkeitsdichtefunktion

$f(x)=\begin{cases} \frac{2(x-a)}{(b-a)(c-a)}, & \text{wenn } a \le x \le c\\ \frac{2(b-x)}{(b-a)(b-c)}, & \text{wenn } c < x \le b. \end{cases}$

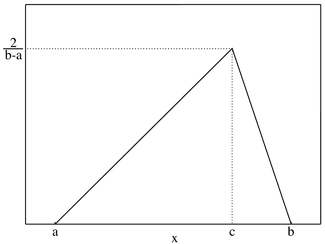
Hierbei bestimmen die Parameter a (minimaler Wert), b (maximaler Wert) und c (wahrscheinlichster Wert) die Gestalt der Dreiecksverteilung 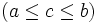$(a\leq c\leq b)$. Die Dichtefunktion sieht wie ein Dreieck aus und gibt dieser Verteilung ihren Namen. Die y-Achse zeigt die jeweilige Wahrscheinlichkeit für einen Wert $x \in \left[a, b\right]$.

Eigenschaften

Verteilungsfunktion

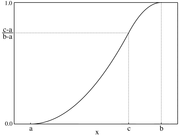
Die Verteilungsfunktion

Die Verteilungsfunktion lautet

$F(x)=\begin{cases} \frac{(x-a)^2}{(b-a)(c-a)}, & \text{wenn } a \le x \le c\\ 1-\frac{(b-x)^2}{(b-a)(b-c)}, & \text{wenn } c < x \le b. \end{cases}$

Erwartungswert

Der Erwartungswert einer dreiecksverteilten Zufallsvariable X lautet

$\operatorname E(X) = \frac{a+b+c}3.$

Varianz

Die Varianz einer dreiecksverteilten Zufallsvariable X ergibt sich zu

$\operatorname{Var}(X) = \frac{a^2+b^2+c^2-ab-ac-bc}{18} = \frac{(a-b)^2+(b-c)^2+(a-c)^2}{36}.$

Siehe auch

• Thomas Simpson

Weblinks

• Eric W. Weisstein: Triangular Distribution auf MathWorld (englisch)
• Universität Konstanz – Interaktive Animation
• Norman L. Johnson, Samuel Kotz: Non-Smooth Sailing or Triangular Distributions Revisited after Some 50 Years. The Statistician, Vol. 48, No. 2 (1999), S. 179–187

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart