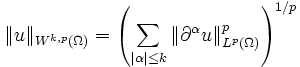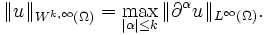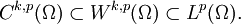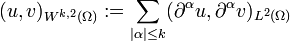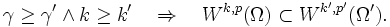- Sobolewscher Einbettungssatz
-
Ein Sobolew-Raum (nach Sergei Lwowitsch Sobolew, in englischer Umschrift Sobolev) ist in der Mathematik ein Funktionenraum von schwach differenzierbaren Funktionen, der zugleich ein Banachraum ist. Das Konzept wurde durch die systematische Theorie der Variationsrechnung zu Anfang des 20. Jahrhunderts wesentlich vorangetrieben. Diese minimiert Funktionale über Funktionen. Heute bilden Sobolew-Räume die Grundlage der Lösungstheorie partieller Differentialgleichungen.
Inhaltsverzeichnis
Sobolew-Räume ganzzahliger Ordnung
Sobolew-Raum (schwache Ableitungen)
Es seien
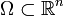 offen und
offen und 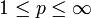 . Der Raum derjenigen reellwertigen Funktionen
. Der Raum derjenigen reellwertigen Funktionen 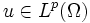 , deren gemischte partielle schwachen Ableitungen bis zur Ordnung k in Lp(Ω) liegen, ist der Sobolew-Raum Wk,p(Ω). Die Schreibweise
, deren gemischte partielle schwachen Ableitungen bis zur Ordnung k in Lp(Ω) liegen, ist der Sobolew-Raum Wk,p(Ω). Die Schreibweise 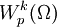 ist ebenfalls üblich.
ist ebenfalls üblich.Sobolew-Norm
Für Funktionen
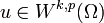 definiert man die Wk,p-Norm durch
definiert man die Wk,p-Norm durchfür
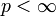 bzw.
bzw.Der Sobolew-Raum Wk,p(Ω) bzw.
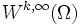 ist bzgl. der jeweiligen Norm vollständig.
ist bzgl. der jeweiligen Norm vollständig.Sobolew-Raum (Topologischer Abschluss)
Betrachten wir nun den Raum der
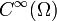 -Funktionen, deren partielle Ableitungen bis zum Grad k in Lp(Ω) liegen, und bezeichnen diesen Funktionenraum mit Ck,p(Ω). Da verschiedene Ck,p-Funktionen nie zueinander Lp-äquivalent (siehe auch Lp-Raum) sind, kann man Ck,p(Ω) in Lp(Ω) einbetten, und es gilt folgende Inklusion
-Funktionen, deren partielle Ableitungen bis zum Grad k in Lp(Ω) liegen, und bezeichnen diesen Funktionenraum mit Ck,p(Ω). Da verschiedene Ck,p-Funktionen nie zueinander Lp-äquivalent (siehe auch Lp-Raum) sind, kann man Ck,p(Ω) in Lp(Ω) einbetten, und es gilt folgende InklusionDer Raum Ck,p(Ω) ist bzgl. der Wk,p-Norm nicht vollständig. Vielmehr ist dessen Vervollständigung gerade Wk,p(Ω). Die partiellen Ableitungen bis zur Ordnung k können als stetige Operatoren auf diesen Sobolew-Raum eindeutig stetig fortgesetzt werden. Diese Fortsetzungen sind gerade die schwachen Ableitungen.
Somit erhält man eine alternative, äquivalente Definition von Sobolevräumen (Satz von Meyers-Serrin).
Eigenschaften
Banachraum / Hilbertraum
Wie bereits erwähnt, ist Wk,p(Ω) mit der Norm
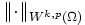 ein Banachraum. Für
ein Banachraum. Für 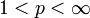 ist er sogar reflexiv.
ist er sogar reflexiv.Für p = 2 wird die Norm durch das Skalarprodukt
induziert. Wk,2(Ω) ist daher ein Hilbertraum, und man schreibt auch Hk(Ω): = Wk,2(Ω).
Einbettungssätze und Sobolewzahl
Mit den obigen Bezeichnungen bildet man die Sobolewzahl
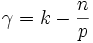 .
.
Mithilfe dieser Zahl lassen sich die Beziehungen zwischen Sobolewräumen einfach darstellen. Sei Ω beschränkt in
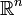 und
und 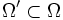 eine Teilmenge oder eine glatte Untermannigfaltigkeit der Dimension n'. Dann gilt der sobolewsche Einbettungssatz
eine Teilmenge oder eine glatte Untermannigfaltigkeit der Dimension n'. Dann gilt der sobolewsche EinbettungssatzDie Teilmengenbeziehung ist als stetige Einbettung zu verstehen. Falls
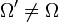 , handelt es sich dabei um den Spuroperator, der eine Verallgemeinerung der Restriktionsabbildung
, handelt es sich dabei um den Spuroperator, der eine Verallgemeinerung der Restriktionsabbildung 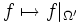 darstellt. Diese kann nicht direkt auf Sobolew-Räume angewendet werden, da wir Funktionen, die fast überall gleich sind, miteinander identifiziert hatten. Der Spuroperator ist als stetige Fortsetzung des Restriktionsoperators für die stetigen Funktionen zu verstehen. Die Einbettung ist kompakt, falls γ > γ' und k > k'.
darstellt. Diese kann nicht direkt auf Sobolew-Räume angewendet werden, da wir Funktionen, die fast überall gleich sind, miteinander identifiziert hatten. Der Spuroperator ist als stetige Fortsetzung des Restriktionsoperators für die stetigen Funktionen zu verstehen. Die Einbettung ist kompakt, falls γ > γ' und k > k'.Sobolew-Raum reellwertiger Ordnung
Oft werden auch Sobolew-Räume mit reellen Exponenten s benutzt. Diese sind über die Fourier-Transformierte der beteiligten Funktionen definiert. Für nichtnegative s ist eine L2(Ω)-Funktion ein Element von
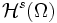 , falls gilt
, falls gilt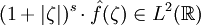 .
.
Literatur
- H.-W. Alt: Lineare Funktionalanalysis, Springer, 5. Auflage, 2006, ISBN 3540341862
- R. A. Adams, J. J. F. Fournier: Sobolev Spaces, Academic Press, 2nd edition, 2003, ISBN 0120441438
- L. C. Evans: Partial Differential Equations, American Mathematical Society, 1998, ISBN 0-8218-0772-2
- L. C. Evans, R. F. Gariepy: Measure Theory and Fine Properties of Functions, CRC, 1991, ISBN 0849371570
- V. Mazja: Sobolev Spaces, Springer, 1985, ISBN 3540135898
- W. P. Ziemer: Weakly Differentiable Functions, Springer, 1989, ISBN 0-387-97017-7
Siehe auch
Wikimedia Foundation.