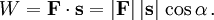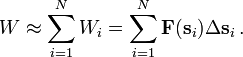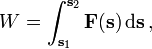- Spannarbeit
-
Physikalische Größe Name Arbeit Formelzeichen der Größe W Größen- und
Einheiten-
systemEinheit Dimension SI Joule 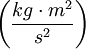
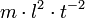
Die Arbeit W (englisch work) ist in der Physik die Energie, die durch eine Kraft längs eines Weges auf einen Körper übertragen wird. In einem konservativen Kraftfeld ist die geleistete Arbeit wegunabhängig.
Die in der Physik verwendeten Begriffe Arbeit, Energie, Kraft und Leistung haben nicht die umgangssprachliche Bedeutung.
Inhaltsverzeichnis
Definition
In der Physik ist Arbeit Kraft mal Weg: Wenn auf einen Körper auf der geraden Strecke vom Punkt A zum Punkt B eine konstante Kraft
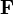 wirkt, dann verrichtet die Kraft am Körper die Arbeit
wirkt, dann verrichtet die Kraft am Körper die ArbeitDabei ist
 der Vektor von A nach B. Das Skalarprodukt der beiden Vektoren
der Vektor von A nach B. Das Skalarprodukt der beiden Vektoren 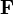 und
und  ist das Produkt ihrer Beträge
ist das Produkt ihrer Beträge  und
und  mal dem Kosinus des Winkels α, den diese einschließen.
mal dem Kosinus des Winkels α, den diese einschließen.Die Bedeutung des physikalischen Begriffs Arbeit beruht auf folgendem Sachverhalt: Bewirkt die betrachtete Kraft die Bewegung des Körpers, so erhöht sich seine kinetische Energie auf dem Weg von A nach B um die an ihm verrichtete Arbeit.
Wirkt die konstante Kraft in Richtung des zurückgelegten Weges, dann ist die Arbeit einfach das Produkt der Beträge
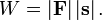
Auf dem Rückweg wird bei unveränderter Kraft die negative Arbeit verrichtet.
Steht die Kraft senkrecht auf dem Weg, wird keine physikalische Arbeit verrichtet. Der physikalische Begriff entspricht also nicht dem alltäglichen Verständnis, nach dem jeder Kofferträger für seine verrichtete Arbeit bezahlt wird.
Wenn die Kraft nicht entlang des gesamten Weges konstant ist oder der Weg nicht gerade ist, so kann man die Arbeit näherungsweise berechnen, indem man den Weg durch einen Streckenzug mit N geraden Teilstücken
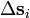 nähert, auf denen die Kraft
nähert, auf denen die Kraft 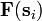 jeweils näherungsweise als konstant angenommen werden kann. Die entlang des gesamten Weges verrichtete Arbeit ergibt sich dann näherungsweise durch Aufsummierung der Arbeiten entlang der einzelnen Wegstücke zu
jeweils näherungsweise als konstant angenommen werden kann. Die entlang des gesamten Weges verrichtete Arbeit ergibt sich dann näherungsweise durch Aufsummierung der Arbeiten entlang der einzelnen Wegstücke zuUm den genauen Wert zu erhalten, wählt man die Wegstücke immer kleiner, so dass ihre Länge gegen Null und ihre Anzahl gegen unendlich geht. Der Grenzwert der Summe ist das Weg- oder Kurvenintegral
wobei
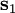 den Anfangs- und
den Anfangs- und 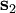 den Endpunkt des Weges bezeichnen.
den Endpunkt des Weges bezeichnen.In einem konservativen Kraftfeld ist die so berechnete Arbeit vom Weg unabhängig und hängt nur vom Anfangs- und Endpunkt ab. Daher ist die Arbeit entlang eines geschlossenen Weges (Anfangspunkt gleich Endpunkt) in einem konservativen Kraftfeld gleich Null.
Beispiele mechanischer Arbeit
- Hubarbeit: Arbeit, die an einem ruhenden Körper der Masse m verrichtet werden muss, um ihn im homogenen Schwerefeld mit Gravitationsbeschleunigung g um die Hubhöhe h zu heben
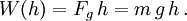
- Die Hubarbeit ist der Unterschied der potentiellen Energie an Ziel und Start.
- Beispiel:
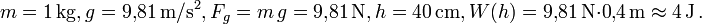
- Spannarbeit
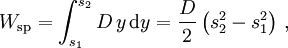
- wobei D die Federkonstante und
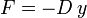 die Federkraft ist. Gegen diese Kraft muss Arbeit am angehängten Pendelkörper verrichtet werden, um ihn von Auslenkung s1 zur Auslenkung s2 (von anfänglicher Ruhe zu schließlicher Ruhe) zu bewegen. Das Koordinatensystem ist so gewählt, dass in der Ruhelage y = 0 gilt.
die Federkraft ist. Gegen diese Kraft muss Arbeit am angehängten Pendelkörper verrichtet werden, um ihn von Auslenkung s1 zur Auslenkung s2 (von anfänglicher Ruhe zu schließlicher Ruhe) zu bewegen. Das Koordinatensystem ist so gewählt, dass in der Ruhelage y = 0 gilt. - Die Spannarbeit zählt wie die Volumenarbeit zu Arbeit, die bei Verformungen verrichtet werden muss.
Siehe auch
- Energie • Potential (Physik)
- Feld (Physik) • Raumkurve
- Thermodynamik
- elektrische Arbeit
- Volumenarbeit
- Federarbeit
- Muskelarbeit
Literatur
- Bärbel Grimm u. A.: Das neue Tafelwerk - Sekundarstufe. Volk und Wissenverlag, 1995, ISBN 3-06-000726-8
- Christian Gerthsen, Dieter Meschede, Helmut Vogel (Herausgeber bis zur 20. Auflage): Physik, 23. Auflage, Springer Verlag, Berlin 2006, ISBN 3-540-25421-8, E-Book 9783540299738
Weblinks
Wikimedia Foundation.