Sprungbrettmethode

Die Zyklenmethode bzw. Stepping-Stone-Methode ist ein numerisches Verfahren, mit dem man (bei gegebener Ausgangs-Basislösung) ein Standard-Transportproblem lösen kann.

Es sind für ein Gut eine bestimmte Anzahl n Anbieter A_i (i = 1,...,n) und eine bestimmte Anzahl m Empfänger B_j (j = 1,...,m) gegeben. Im Standardfall ist die gesamte nachgefragte Menge gleich der gesamten angebotenen. Für den Transport einer Einheit x_ij zwischen A_i und B_j fallen Kosten c_ij an. Das Problem besteht darin, die von A_i nach B_j gelieferte Menge x_ij so festzulegen, dass die Gesamtransportkosten minimiert werden.

Da es sich um ein Verbesserungsverfahren handelt, wird zunächst mit einem Eröffnungsverfahren (z. B. dem Matrixminimumverfahren, dem Nord-West-Ecken-Verfahren, dem Zeilen- oder Spaltenfolge-Verfahren, der Zeilen-Spalten-Sukzession, der Vogelschen Approximationsmethode oder der Russell´schen Approximationsmethode) eine zulässige Anfangsbasislösung 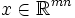$x \in \mathbb{R}^{mn}$ bestimmt. Variablen der Basislösung, die im Eröffnungsverfahren a priori gleich Null gesetzt wurden sind die Nichtbasisvariablen, die restlichen die Basisvariablen des zu Grunde liegenden Gleichungssystems. Die Stepping-Stone-Methode verringert dann iterativ durch Austausch einer Nichtbasisvariablen mit einer Basisvariablen die Gesamtkosten. Kann keine Verbesserung mehr erzielt werden ist eine Optimallösung gefunden.

Verfahren

Das Optimierungsverfahren wird iterativ durchgeführt. In jedem Schritt werden alle Nichtbasisvariablen im Hinblick auf das Kostensenkungspotential überprüft. Für jede Nichtbasisvariable x_ij wird dazu analysiert, wie sich die Gesamtkosten ändern würden, wenn eine Einheit des Gutes von A_i nach B_j transportiert werden würde. Dazu wird zu der Zelle (i,j) einer jeden Nichtbasisvariablen x_ij zusammen mit den Zellen der Basisvariablen ein elementarer Kreis bestimmt. Die Zellen z₁ bis z_k 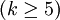$(k \geq 5)$ bilden dabei einen elementaren Kreis, wenn z₁ = z_k, zwei aufeinanderfolgende Zellen z_i und z_{i + 1} in der gleichen Zeile oder Spalte des Tableau liegen und in jeder Spalte und Zeile höchstens zwei Zellen des elementaren Kreises sind. Seien jetzt die Zellen 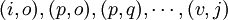$(i,o),(p,o),(p,q),\cdots , (v,j)$ der Basisvariablen, die zusammen mit der Zelle (i,j) der Nichtbasisvariablen x_ij einen elementaren Kreis beschreiben, bestimmt. Dann lassen sich die Gesamtkosten um 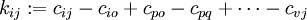$k_{ij}:=c_{ij}-c_{io}+c_{po}-c_{pq}+ \cdots -c_{vj}$ pro zusätzlicher von A_i nach B_j transportierter Einheit verbessern. Ist k_ij positiv, würde dies zu einer Erhöhung der Gesamtkosten führen, ist k_ij gleich Null, würden sich die Gesamtkosten nicht ändern. Um mit möglichst wenig Iterationen zur Optimallösung zu kommen wird deswegen die Nichtbasisvariable x_ij mit dem negativsten k_ij als neue Basisvariable aufgenommen und mit der wertmässig kleinsten Basisvariable x_ab, deren Kosten bei der Bestimmung von k_ij mit negativem Faktor einging, ersetzt. Die Nichtbasisvariable x_ij wird neue Basisvariable mit dem Wert von x_ab und x_ab wird neue Nichtbasisvariable mit Wert Null. Damit die neue Basislösung zulässig bleibt, werden die übrigen Basisvariablen des elementaren Kreises um den Wert der ursprünglichen Basisvariable x_ab erhöht bzw. (wenn die zugehörigen Kosten bei der Bestimmung von k_ij mit negativem Faktor eingingen) verringert. Alle anderen Variablen x_kl bleiben unverändert. Das Verfahren wird solange wiederholt, bis alle (in jeder Iteration neu zu bestimmenden) k_ij größer oder gleich Null sind, die Gesamtkosten also nicht mehr verringert werden können und die Lösung damit optimal ist.

Beispiel

Es liegt folgendes, tabellarisch zusammengefasstes Transportproblem vor, wobei es zwei Angebote A₁ und A₂ und drei Bedarfsanmeldungen B₁, B₂ und B₃ gibt und x_ij hier die von i nach j gelieferte Menge bezeichnet.

   |B 1  B2  B3 |
---------------------
A1 | x11 x12 x13 | 12
A2 | x21 x22 x23 | 8
---------------------
   |  4  10   6 | 20

Die Kosten c_ij, die für den Transport einer Einheit von i nach j entstehen, sind in der folgenden Tabelle aufgeführt.

 cij|B 1  B2  B3 |
---------------------
A1 |  7  4  3 | 12
A2 |  5  5  6 | 8
---------------------
   |  4 10  6 | 20

Für die praktische Durchführung werden die Transportmengen in die Tabelle eingetragen und die entsprechenden Kosten werden in jeder Zelle oben links mit aufgeführt. Es wurde hier als Anfangslösung das Nord-West-Ecken-Verfahren verwendet. Es ergibt sich also

   |B 1| B2| B3 |
---------------------
A1 |7/ |4/ |3/ |
   |  4|  8|  0| 12
---------------------
A2 |5/ |5/ |6/ | 
   |  0|  2|  6|  8
---------------------
   |  4| 10|  6| 20

und man erhält Gesamtkosten von

$4 \cdot 7 + 8 \cdot 4 + 0 \cdot 3 + 0 \cdot 5 + 2 \cdot 5 + 6 \cdot 6 = 106$.

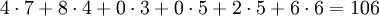Es wird nun versuchsweise der Inhalt von Zelle 13 um Eins erhöht. Man sieht, wie sich die Änderungen kreisförmig fortpflanzen.

   | B1 | B2 | B3 |
---------------------
A1 |7/  |4/  |3/  |
   |   4|-1 8|+1 0| 12
---------------------
A2 |5/  |5/  |6/  | 
   |   0|+1 2|-1 6|  8
---------------------
   |   4|  10|   6| 20

Ebenso ändern die Kosten pro Einheit:

dc₁₃ = + 3 − 4 + 5 − 6 = − 2.

Es würden also die Kosten um 2 Euro sinken, wenn A₁ eine Einheit zu B₃ transportieren würde.

Eine Analyse von Zelle 21 ergibt:

   | B1 | B2 | B3 |
---------------------
A1 |7/  |4/  |3/  |
   |-1 4|+1 8|   0| 12
---------------------
A2 |5/  |5/  |6/  | 
   |+1 0|-1 2|   6|  8
---------------------
   |   4|  10|   6| 20

Die Kosten pro Einheit ändern sich um

dc₂₁ = + 5 − 5 + 4 − 7 = − 3.

Es würden also die Kosten um 3 Euro sinken, wenn A₂ eine Einheit zu B₁transportieren würde. Man sieht, dass die letztere Änderung die Kosten mehr senkt. Es wird nun so viel wie erlaubt in Zelle 21 transferiert, wobei die Vorzeichen der Einsen angeben, ob der Betrag addiert oder subtrahiert wird.

   |B 1| B2| B3 |
---------------------
A1 |7/ |4/ |3/ |
   |  2| 10|  0| 12
---------------------
A2 |5/ |5/ |6/ | 
   |  2|  0|  6|  8
---------------------
   |  4| 10|  6| 20

Es konnten nur maximal zwei Einheiten in die Zelle 21 transferiert werden, weil sonst die Zelle 22 negativ geworden wäre. Die Zelle 21 ist jetzt Basisvariable, die Zelle 22 Nichtbasisvariable.

Es werden nun wieder alle Nichtbasisvariablen untersucht. Für die Zelle 13 ergibt sich jetzt der Kreis der Zellen 13 - 11 - 21 - 23, denn Zelle 22 ist Nichtbasisvariable und kann nicht simultan mit Zelle 13 geändert werden. Zelle 22 wird also übersprungen. Man erhält dann

dc₁₃ = 3 − 7 + 5 − 6 = − 5

und

dc₂₂ = 5 − 4 + 7 − 5 > 0.

Hier steigen die Kosten bei Änderung von Zelle 22. Es wird also Zelle 13 verändert. Es können maximal zwei Einheiten nach Zelle 13 transferiert werden und man erhält nun

   |B 1| B2| B3 |
---------------------
A1 |7/ |4/ |3/ |
   |  0| 10|  2| 12
---------------------
A2 |5/ |5/ |6/ | 
   |  4|  0|  4|  8
---------------------
   |  4| 10|  6| 20

Es werden wieder alle Nichtbasisvariablen untersucht. Für die Zelle 11 ergibt sich jetzt der Kreis der Zellen 11 - 13 - 23 - 21, denn Zelle 22 ist Nichtbasisvariable und wird übersprungen. Man erhält dann

dc₁₁ = 7 − 3 + 4 − 6 > 0.

Die Nichtbasisvariable in Zelle 22 erzeugt hingegen

dc₂₂ = 5 − 4 + 3 − 6 = − 2.

Es wird also Zelle 22 verändert. Es können maximal vier Einheiten nach Zelle 22 transferiert werden und man erhält

   |B 1| B2| B3 |
---------------------
A1 |7/ |4/ |3/ |
   |  0|  6|  6| 12
---------------------
A2 |5/ |5/ |6/ | 
   |  4|  4|  0|  8
---------------------
   |  4| 10|  6| 20

Eine neue Iteration ergibt nur noch Kostensteigerungen, also ist das Verfahren beendet. Man erhält Gesamtkosten von

$0 \cdot 7 + 6 \cdot 4 + 6 \cdot 3 + 4 \cdot 5 + 4 \cdot 5 + 0 \cdot 6 = 82$

im Gegensatz zu 106 der Startlösung.

Bemerkungen

• Ist gesamte nachgefragte Menge kleiner als die gesamte angebotene Menge, kann durch Einführen eines fiktiven Nachfragers B_{m + 1}, der das überschüssige Angebot nachfragt und Transportkosten c_{i,m + 1} = 0 für alle Anbieter A_i hat, das Transportproblem in ein Standardtransportmodell transformiert werden und damit ebenfalls mit der Stepping-Stone-Methode gelöst werden.

• Ist bei der Optimallösung eine mögliche Kostenveränderung k_ij bei Aufnahme der Variable x_ij gleich Null, bedeutet dieses, dass der Wert der zugehörige Nichtbasisvariable mit dem einer Basisvariablen ausgetauscht werden kann, ohne dass sich die Gesamtkosten ändern und die Optimallösung damit nicht eindeutig ist.

• Ein ähnliche Methode zur Verbesserung einer Anfangsbasislösung und finden der Optimallösung ist die MODI-Methode. Dabei werden die Kostenveränderungen k_ij mit geringerem Rechenaufwand (aber identischen Werten) als bei der Stepping-Stone-Methode bestimmt.

• Gibt es mehrere negative k_ij kann statt dem betragsmäß größtem auch jene zugehörige Nichtbasisvariable ausgewählt werden, die zu einer maximalen Verbesserung der Kostensumme führt oder eine zufällig davon ausgewählt werden.