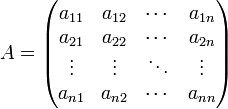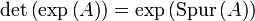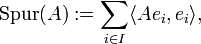- Spurfunktion
-
Die Spur (Spurfunktion, Spurabbildung) ist ein Konzept in den mathematischen Teilgebieten der Linearen Algebra, der Funktionalanalysis und wird auch in der Theorie der Körper und Körpererweiterungen verwendet.
Inhaltsverzeichnis
Die Spur in der linearen Algebra
In der linearen Algebra bezeichnet man als die Spur einer quadratischen
 -Matrix A über einem Körper K die Summe der Diagonalelemente dieser Matrix. Für die Matrix
-Matrix A über einem Körper K die Summe der Diagonalelemente dieser Matrix. Für die Matrixist also
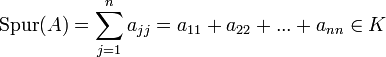 .
.
Statt
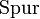 schreibt man auch spur, Sp oder sp oder vom englischen Begriff trace abgeleitet auch Trace, trace, Tr oder tr.
schreibt man auch spur, Sp oder sp oder vom englischen Begriff trace abgeleitet auch Trace, trace, Tr oder tr.Gilt
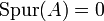 , so bezeichnet man die Matrix als spurfrei.
, so bezeichnet man die Matrix als spurfrei.Eigenschaften
- Die Spur einer reellen oder komplexen Matrix ist die Summe ihrer Eigenwerte (aller Eigenwerte mit Vielfachheit, auch der komplexen). Im charakteristischen Polynom tritt sie als zweithöchster Koeffizient auf. Sie hat also eine ähnliche Bedeutung wie die Determinante, die das Produkt aller Eigenwerte ist.
- Die Spur ist eine lineare Abbildung, das heißt, für
 -Matrizen A und B sowie
-Matrizen A und B sowie 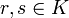 gilt
gilt
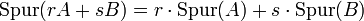 .
.
- Unter der Spur dürfen Matrizen
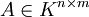 und
und 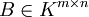 vertauscht werden, das heißt
vertauscht werden, das heißt
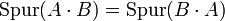 .
.
- Aus der letzten Eigenschaft folgt die Invarianz der Spur unter zyklischen Vertauschungen, also für
 -Matrizen A, B und C
-Matrizen A, B und C
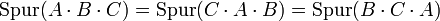 .
.
- Weiter folgt hieraus, dass die Spur invariant unter Basistransformationen ist. Für eine
 -Matrix A und eine invertierbare
-Matrix A und eine invertierbare  -Matrix B gilt
-Matrix B gilt
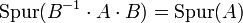 .
.
- Sind A und B
 -Matrizen, wobei A positiv definit und B nicht negativ ist, so gilt
-Matrizen, wobei A positiv definit und B nicht negativ ist, so gilt
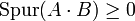 .
.
- Die Spur einer reellen oder komplexen idempotenten Matrix A ist gleich ihrem Rang:
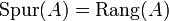 .
.
(Für Matrizen mit Einträgen aus einem anderen Körper gilt diese Identität nur modulo der Charakteristik des Körpers.)
- Für alle reellen oder komplexen
 -Matrizen A gilt
-Matrizen A gilt
- Mittels
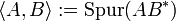 lässt sich das Hilbert-Schmidt-Skalarprodukt auf den (reellen oder komplexen)
lässt sich das Hilbert-Schmidt-Skalarprodukt auf den (reellen oder komplexen)  -Matrizen definieren, so dass wegen der Cauchy-Schwarzschen Ungleichung gilt
-Matrizen definieren, so dass wegen der Cauchy-Schwarzschen Ungleichung gilt
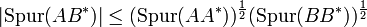 .
.
Spur eines Endomorphismus
Ist V ein endlichdimensionaler Vektorraum und
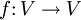 eine lineare Abbildung, also ein Endomorphismus von V, so definiert man die Spur von f als die Spur einer Darstellungsmatrix von f bezüglich einer beliebigen Basis von V. Nach den obengenannten Eigenschaften ist die Spur unabhängig von der Wahl dieser Basis.
eine lineare Abbildung, also ein Endomorphismus von V, so definiert man die Spur von f als die Spur einer Darstellungsmatrix von f bezüglich einer beliebigen Basis von V. Nach den obengenannten Eigenschaften ist die Spur unabhängig von der Wahl dieser Basis.Die Spur in der Funktionalanalysis
Das Konzept der Spur in der linearen Algebra kann auch auf unendlichdimensionale Räume ausgedehnt werden. Ist H ein Hilbertraum mit einer Orthonormalbasis
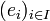 , dann definiert man für einen Operator
, dann definiert man für einen Operator 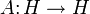 die Spur mittels
die Spur mittelsfalls die Summe existiert. Operatoren, für die dies der Fall ist (diese sind immer kompakt), nennt man Spurklasseoperatoren. Viele Eigenschaften der Spur aus der linearen Algebra übertragen sich unmittelbar auf Spurklasseoperatoren.
Die Spur in Körpererweiterungen
Ist L / K eine endliche Körpererweiterung, dann ist die Spur eine K-lineare Abbildung von L nach K. Fasst man L als K-Vektorraum auf, dann definiert man die Spur eines Elementes
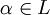 als die Spur der Darstellungsmatrix der Abbildung
als die Spur der Darstellungsmatrix der Abbildung 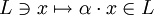 .
.
Wikimedia Foundation.