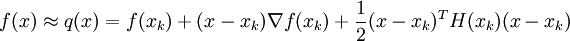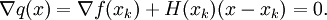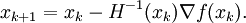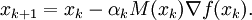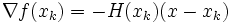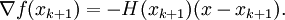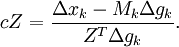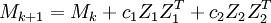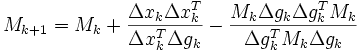Sqp

Quasi-Newton-Verfahren sind eine Klasse von numerischen Verfahren zur Lösung nichtlinearer Minimierungsprobleme. Die Verfahren basieren auf dem Newton-Verfahren, berechnen die Inverse der Hesse-Matrix jedoch nicht direkt, sondern nähern sie lediglich an, um den Rechnenaufwand pro Iteration zu verkleinern. Der erste Algorithmus wurde von W.C Davidon, einem Physiker am Argonne National Laboratory Mitte der 1950er Jahre entwickelt. Die bekanntesten Algorithmen sind Broyden-Fletcher-Goldfarb-Shanno (BFGS) und Davidon-Fletcher-Powell (DFP).

Grundlegender Algorithmus

Eine zweifach differenzierbare Funktion 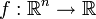$f:\mathbb{R}^n \rightarrow \mathbb{R}$ wird mit einer Taylor-Entwicklung bis zum zweiten Grad angenähert.

$f(x) \approx q(x) = f(x_k) + (x-x_k)\nabla f(x_k) + {1 \over 2} (x-x_k)^T H(x_k)(x-x_k)$

Die Ableitung der Funktion q muss für ein Minimum null ergeben. Daraus folgt :

$\nabla q(x) = \nabla f(x_k) + H(x_k)(x-x_k) = 0.$

Falls die Hesse-Matrix H(x_k) positiv definit ist, lässt sich mit dem Newton-Verfahren der Punkt x_k berechnen.

$x_{k+1} = x_k - H^{-1}(x_k) \nabla f(x_k).$

Problematisch ist hier, dass die Inverse der Hesse-Matrix berechnet und diese positiv definit sein muss. Das Quasi-Newton-Verfahren ersetzt H ^{− 1}(x_k) durch ein Skalar α und eine Matrix M_k

$x_{k+1} = x_k - \alpha_k M(x_k) \nabla f(x_k).$

Die Ableitungs-Gleichung von oben ergibt umgeformt für x_k und x_{k + 1}

$\nabla f(x_k) = - H(x_k)(x-x_k)$

$\nabla f(x_{k+1}) = - H(x_{k+1})(x-x_{k+1}).$

Daraus lässt sich Δg_k herleiten :

$\Delta g_k = \nabla f(x_{k+1}) - \nabla f(x_k)$

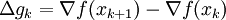
Δg_k = − H(x_{k + 1})(x − x_{k + 1}) + H(x_k)(x − x_k).

Man nimmt nun an, dass die Hesse-Funktion für x_k und x_{k + 1} in etwa dasselbe sind und folgert daraus :

$\Delta g_k \approx - H(x_{k+1})(x_k-x_{k+1})$

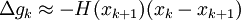
M_{k + 1}Δg_k = x_{k + 1} − x_k.

Für M_{k + 1} wählt man einen Korrekturterm der Form cZZ^T:

M_{k + 1} = M_k + cZZ^T

M_{k + 1}Δg_k = M_kΔg_k + cZZ^TΔg_k = x_{k + 1} − x_k = Δx_k.

Die Gleichung lässt sich umstellen, so dass

$cZ = {{\Delta x_k - M_k \Delta g_k} \over {Z^T \Delta g_k}}.$

Somit gilt

Z = Δx_k − M_kΔg_k

$c = {{1} \over {Z^T \Delta g_k}}.$

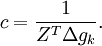
So lässt sich die Matrix M_{k + 1} eindeutig bestimmen, jedoch ist diese mit nur einem Korrekturterm nicht immer positiv definit.

Davidon-Fletcher-Powell (DFP)

Die Matrix M_{k + 1} wird mit der Matrix M_k und zwei Korrekturtermen approximiert:

$M_{k+1} = M_k + c_1 Z_1 Z_1^T + c_2 Z_2 Z_2^T$

$M_{k+1} = M_k + {{\Delta x_k \Delta x_k^T} \over {\Delta x_k^T \Delta g_k }} - {{M_k \Delta g_k \Delta g_k^T M_k} \over {\Delta g_k^T M_k \Delta g_k}}$

Eigenschaften

Falls f eine quadratische Funktion ist, dann konvergiert der Algorithmus in n Iterationen. Für alle anderen Funktionen gilt :

f(x_{k + 1}) < f(x_k).

Literatur

• William C. Davidon, Variable Metric Method for Minimization, SIOPT Volume 1 Issue 1, Pages 1-17, 1991.
• Nocedal, Jorge & Wright, Stephen J.: Numerical Optimization, Springer-Verlag, 1999 ISBN 0-387-98793-2.
• Edwin K.P.Chong and Stanislaw H.Zak: An Introduction to Optimization, 2ed, John Wiley & Sons Pte. Ltd. August 2001.
• P. Gill, W. Murray & M. Wright, "Practical Optimization", 1981