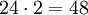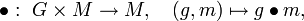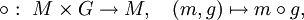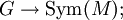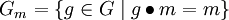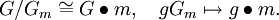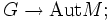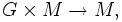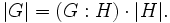- Stabilisator (Mathematik)
-
In der Mathematik tritt der Begriff der Operation (auch Wirkung oder Aktion) bei der Betrachtung von Gruppen und ihrem Zusammenspiel mit anderen Strukturen auf.
Inhaltsverzeichnis
Einführendes Beispiel: Operation der Symmetriegruppe eines Würfels auf den Raumdiagonalen
ABCDEFGH seien die Ecken eines Würfels in der üblichen Bezeichnung, d. h. ABCD und EFGH sind gegenüberliegende Flächen (siehe erstes Bild). Die Drehung des Würfels um die Achse, die die Mittelpunkte dieser beiden Flächen verbindet (zweites Bild), induziert die folgenden Vertauschung der Ecken:
Durch die Drehung werden auch die Raumdiagonalen vertauscht, nämlich
Es gibt aber auch Symmetrieabbildungen des Würfels, die die Raumdiagonalen nicht untereinander vertauschen, nämlich die Punktspiegelung am Mittelpunkt (drittes Bild): Sie entspricht
Dabei wird jede einzelne Raumdiagonale zwar gespiegelt, aber auf sich selbst abgebildet.
Man sagt: Die Gruppe der Symmetrieabbildungen des Würfels operiert auf der Menge der Raumdiagonalen.
Dieser Umstand erlaubt es, Rückschlüsse auf die Gruppe zu ziehen. Dazu stellt man fest, dass es zu jedem Paar von Raumdiagonalen eine Symmetrieabbildung gibt, die diese beiden vertauscht und die anderen beiden fest lässt, nämlich die Spiegelung an der Ebene, die die beiden anderen Raumdiagonalen enthält. Aus den allgemeinen Eigenschaften der symmetrischen Gruppe folgt damit, dass es zu jeder Permutation der Raumdiagonalen eine entsprechende Symmetrieabbildung gibt. Da es 4! = 24 dieser Permutationen gibt und genau zwei Symmetrieabbildungen, die alle Raumdiagonalen festlassen (nämlich die Identität und die oben genannte Punktspiegelung), kann man schließen, dass es insgesamt
Symmetrieabbildungen des Würfels gibt, ohne jede von ihnen einzeln zu kennen. (Für eine genauere Analyse der Gruppenstruktur siehe Oktaedergruppe.)
Definition
Eine Linksoperation (auch Linkswirkung oder Linksaktion) einer Gruppe
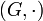 auf einer Menge M ist eine Abbildung
auf einer Menge M ist eine Abbildungdie die folgenden Eigenschaften erfüllt:
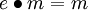 für alle
für alle 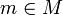 ; dabei ist
; dabei ist 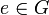 das neutrale Element.
das neutrale Element. für alle
für alle 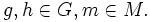
Entsprechend ist eine Rechtsoperation eine Abbildung
die die Eigenschaften
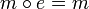 für alle
für alle 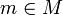
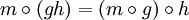 für alle
für alle 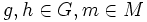
erfüllt.
Eine Gruppenoperation oder Gruppenaktion ist eine Links- oder Rechtsoperation.
(Eine Menge M, auf der eine Gruppe G operiert, wird manchmal auch G-Menge genannt.)
Eine Linksoperation kann auch definiert werden als ein Gruppenhomomorphismus
dabei ist
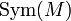 die Gruppe der bijektiven Abbildungen
die Gruppe der bijektiven Abbildungen 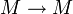 , auch als symmetrische Gruppe auf M bezeichnet. Wichtig ist dabei, dass diese Abbildungen von links wirken, d. h.
, auch als symmetrische Gruppe auf M bezeichnet. Wichtig ist dabei, dass diese Abbildungen von links wirken, d. h.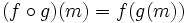 für
für 
Ist
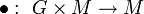 eine Linksoperation wie oben, so entspricht ihr der Homomorphismus
eine Linksoperation wie oben, so entspricht ihr der HomomorphismusBegriffe im Zusammenhang mit Gruppenoperationen
Bahn
Es sei M eine Menge mit einer G-Linksoperation.
- Für ein
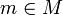 nennt man
nennt man
-
- die Bahn oder den Orbit von m. Die Bahnen bilden eine Partition von M. Die Anzahl der Elemente einer Bahn (bzw. ihre Mächtigkeit) wird auch die Länge der Bahn genannt.
- Die Bahnen sind die Äquivalenzklassen bezüglich der Äquivalenzrelation:
-
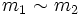 , falls es ein
, falls es ein 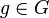 gibt, für das
gibt, für das 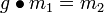 gilt.
gilt.
- Die Menge der Äquivalenzklassen wird mit
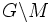 bezeichnet und Bahnenraum genannt. (Für eine Rechtsoperation ist die Notation M / G.)
bezeichnet und Bahnenraum genannt. (Für eine Rechtsoperation ist die Notation M / G.)
Stabilisator
- Für ein
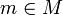 nennt man
nennt man
-
- den Stabilisator oder die Isotropiegruppe oder die Fixgruppe oder die Standuntergruppe von m. Gm ist eine Untergruppe von G. Die Operation definiert eine kanonische Bijektion zwischen den Nebenklassen des Stabilisators und der Bahn:
- Ist
 eine Teilmenge und
eine Teilmenge und 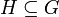 eine Untergruppe, und gilt
eine Untergruppe, und gilt
-
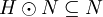 mit
mit 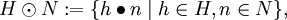
- so sagt man, dass N stabil unter H ist oder dass N von H stabilisiert wird. Es gilt dann stets sogar
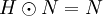 . Der Stabilisator eines Punktes
. Der Stabilisator eines Punktes 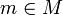 ist also die maximale Untergruppe von G, die {m} stabilisiert.
ist also die maximale Untergruppe von G, die {m} stabilisiert.
- Gibt es zu je zwei Elementen
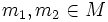 ein
ein 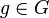 , so dass
, so dass 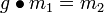 gilt, so heißt die Operation transitiv. In diesem Fall gibt es nur eine einzige Bahn.
gilt, so heißt die Operation transitiv. In diesem Fall gibt es nur eine einzige Bahn.
- Gibt es sogar zu je vier Elementen
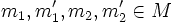 mit
mit 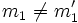 und
und 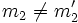 ein
ein 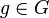 , so dass sowohl
, so dass sowohl 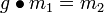 als auch
als auch 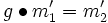 gilt, so heißt die Operation zweifach transitiv. Analog hierzu: dreifach transitiv usw.
gilt, so heißt die Operation zweifach transitiv. Analog hierzu: dreifach transitiv usw.
- Folgt aus
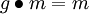 für ein
für ein 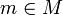 , dass g = e gilt, so heißt die Operation frei. Dies ist äquivalent dazu, dass sämtliche Stabilisatoren trivial sind, d. h. Gm = {e} für alle
, dass g = e gilt, so heißt die Operation frei. Dies ist äquivalent dazu, dass sämtliche Stabilisatoren trivial sind, d. h. Gm = {e} für alle 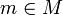 .
.
- Folgt aus
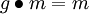 für alle
für alle 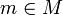 , dass g = e gilt, so heißt die Operation treu bzw. effektiv. Dies ist äquivalent dazu, dass der zugehörige Homomorphismus
, dass g = e gilt, so heißt die Operation treu bzw. effektiv. Dies ist äquivalent dazu, dass der zugehörige Homomorphismus 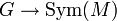 injektiv ist.
injektiv ist.
- Wenn N eine weitere Menge mit einer G-Linksoperation * ist und
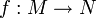 eine Abbildung, so dass für alle
eine Abbildung, so dass für alle 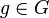 und für alle
und für alle 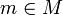 gilt
gilt
-
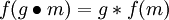 ,
,
- dann heißt f G-äquivariante Abbildung oder auch Homomorphismus von G-Mengen.
Operationen auf allgemeineren Objekten
Ist M eine abelsche Gruppe, so ist eine Linksoperation einer Gruppe G auf M ein Gruppenhomomorphismus
dabei ist
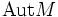 die Gruppe der Automorphismen von M als abelsche Gruppe. Äquivalent dazu kann man diese Operation auch beschreiben durch eine Abbildung
die Gruppe der Automorphismen von M als abelsche Gruppe. Äquivalent dazu kann man diese Operation auch beschreiben durch eine Abbildungdie eine Linksoperation auf M als Menge definiert und zusätzlich kompatibel zur Struktur von M ist, d. h.
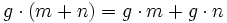 für
für 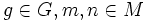
erfüllt.
Eine abelsche Gruppe mit einer G-Operation wird auch G-Modul genannt.
Ist allgemein M ein Objekt einer beliebigen Kategorie, so kann eine Operation einer (abstrakten) Gruppe G auf M definiert werden als ein Gruppenhomomorphismus
dabei ist
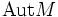 die Gruppe der Automorphismen von M im kategorientheoretischen Sinne. Die oben genannten Operationen von Gruppen auf Mengen oder abelschen Gruppen sind Spezialfälle.
die Gruppe der Automorphismen von M im kategorientheoretischen Sinne. Die oben genannten Operationen von Gruppen auf Mengen oder abelschen Gruppen sind Spezialfälle.Beispiele
Linkstranslation
(Einiges davon könnte z. B. in einen Artikel Faktorgruppe.)
Ein Beispiel einer Operation ist die Linkstranslation (Linksmultiplikation) innerhalb einer Gruppe
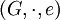 . Definiert man die Wirkung
. Definiert man die Wirkung 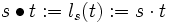 , dann operiert G auf sich selbst, denn es ist
, dann operiert G auf sich selbst, denn es ist  und
und 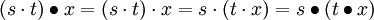 .
.T ist die Abbildung, die jedem Element s die Linkstranslation mit s,
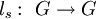 , zuordnet. Diese Zuordnung T ist injektiv, man erhält hieraus den
, zuordnet. Diese Zuordnung T ist injektiv, man erhält hieraus den- Satz von Cayley: Jede endliche Gruppe der Ordnung n ist isomorph zu einer Untergruppe der symmetrischen Gruppe Sn.
Analoges gilt auch für die Rechtstranslation
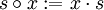 .
.Betrachtet man eine Untergruppe H von G, dann operiert auch H durch die Linkstranslation auf G. Die Bahn
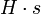 eines Elements s von G heißt Rechtsnebenklasse von s. Die Menge aller Rechtsnebenklassen bezeichnet man mit
eines Elements s von G heißt Rechtsnebenklasse von s. Die Menge aller Rechtsnebenklassen bezeichnet man mit- H\G,
ihre Mächtigkeit mit
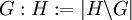 .
.
Da die Linkstranslation eine Bijektion ist, gilt | Hs | = | H | für jedes s aus G. Daraus folgt mit der Bahnengleichung (s.u.) der
- Satz von Euler-Lagrange: Für jede Untergruppe H einer endlichen Gruppe G gilt
- Insbesondere ist die Ordnung von H ein Teiler der Ordnung von G.
Betrachtet man stattdessen die Rechtstranslation von H auf G, dann nennt man die Bahn sH von s seine Linksnebenklasse. Man beachte, dass im allgemeinen nicht sH = Hs sein muss. Die Menge aller Linksnebenklassen bezeichnet man mit G / H. Man kann zeigen, dass es genauso viele Linksnebenklassen wie Rechtsnebenklassen gibt, dass also
- G:H = | G / H | .
Eine Untergruppe H von G heißt Normalteiler, wenn sH = Hs für alle s aus G gilt. Ist H ein Normalteiler von G, dann wird durch
eine wohldefinierte Verknüpfung von G/H definiert, mit der G/H eine Gruppe ist, man nennt sie die Faktorgruppe G modulo H.
Konjugation
Eine Gruppe G operiert auf sich durch die Konjugation s.t := fs(t) := s-1*t*s. Die Automorphismen fs(t) = s-1*t*s heißen innere Automorphismen, die Menge aller inneren Automorphismen bezeichnet man mit Inn(G).
Automorphismengruppe einer Körpererweiterung
Ist L/K eine Körpererweiterung, dann bezeichnet man mit Aut(L/K) die Gruppe aller Automorphismen von L, die K punktweise fest lassen. Diese Gruppe operiert auf L durch f.x := f(x). Jede Bahn besteht aus den in L liegenden Nullstellen eines Polynoms mit Koeffizienten in K, das über K irreduzibel ist. Elemente derselben Bahn nennt man hier konjugiert über K, sie haben dasselbe Minimalpolynom über K.
Andere Beispiele
Man kann die skalare Multiplikation eines Vektorraums V mit seinem Grundkörper K als Operation auffassen: x.v := x*v. Dabei ist die multiplikative Gruppe K* die Gruppe G und V die Menge M.
Eigenschaften
Operiert die Gruppe
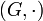 auf M, dann bilden die Bahnen eine Zerlegung von M, das heißt: Je zwei Bahnen sind disjunkt oder gleich, und jedes Element von M liegt in einer Bahn. Denn man kann die folgende Äquivalenzrelation "
auf M, dann bilden die Bahnen eine Zerlegung von M, das heißt: Je zwei Bahnen sind disjunkt oder gleich, und jedes Element von M liegt in einer Bahn. Denn man kann die folgende Äquivalenzrelation "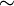 " definieren:
" definieren:- Sind x,y aus M, dann ist
 , falls ein s in G existiert, so dass
, falls ein s in G existiert, so dass 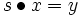 ist.
ist.
Die Äquivalenzklassen dieser Relation sind genau die Bahnen. Daraus folgt die
- Bahnengleichung: Die Mächtigkeit von M ist gleich der Summe über die Länge aller Bahnen.
Genauer gilt der Bahnensatz: Ist x aus M, dann ist die Abbildung
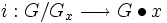 mit
mit 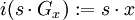 eine Bijektion.
eine Bijektion.Aus dieser Bijektion folgt für eine endliche Gruppe G die Bahnformel
 .
.
Insbesondere ist die Länge jeder Bahn ein Teiler der Ordnung von G.
Weblinks
Wikimedia Foundation.