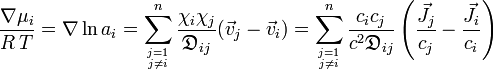Stefan-Maxwell-Diffusion

Als Maxwell-Stefan-Diffusion (auch Stefan-Maxwell-Diffusion) wird ein Modell zur Beschreibung der Diffusion in Multikomponentensystemen bezeichnet. Die Gleichungen, die diese Transportvorgänge beschreiben, wurden von James Clerk Maxwell^[1] für verdünnte Gase und Josef Stefan^[2] für Flüssigkeiten parallel und unabhängig von einander entwickelt. Die Maxwell-Stefan-Gleichung lautet^[3][4][5]:

$\frac{\nabla \mu_i}{R\,T} = \nabla \ln a_i =\sum_{j=1\atop j\neq i}^{n}{\frac{\chi_i \chi_j}{\mathfrak{D}_{ij}}(\vec v_j-\vec v_i)} =\sum_{j=1\atop j\neq i}^{n}{\frac{c_ic_j}{c^2\mathfrak{D}_{ij}}\left(\frac{\vec J_j}{c_j}-\frac{\vec J_i}{c_i}\right)}$

• ∇: Nabla-Operator
• χ: Stoffmengenanteil
• μ: chemisches Potential
• a: Aktivität
• i, j: Indizes für Komponente i und j
• n: Anzahl der Komponenten
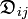• $\mathfrak{D}_{ij}$: Maxwell-Stefan-Diffusionskoeffizienten
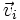• $\vec v_i$: Geschwindigkeit der Komponente i
• c_i: Stoffmengenkonzentration der Komponente i
• c: Gesamtstoffmengenkonzentration
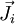• $\vec J_i$: Stofffluss der Komponente i

Die Gleichung geht vom Steady-State, also der Abwesenheit von Geschwindigkeitsgradienten aus.

Die Grundannahme der Theorie ist, dass eine Abweichung vom Gleichgewicht zwischen molekularer Reibung und thermodynamischen Interaktionen zum Diffusionsfluss führt.^[6] Die molekulare Reibung zwischen zwei Komponenten ist proportional zu ihrem Geschwindigkeitsunterschied und den Stoffmengenanteilen. Im einfachsten Fall ist der Gradient des chemischen Potentials die Antriebskraft der Diffusion. Für komplexere Systeme, wie beispielsweise elektrolytische Lösungen, und weitere Antriebskräfte, wie beispielsweise Druckgradienten, muss die Gleichung um Terme für zusätzliche Interaktionen erweitert werden.

Ein großer Nachteil der Maxwell-Stefan-Theorie ist, dass die Diffusionskoeffizienten, mit Ausnahme der Diffusion verdünnter Gase, nicht den Fickschen Diffusionskoeffizienten entsprechen und daher nicht tabelliert sind. Auch sind die Diffusionskoeffizienten nur für den binären und ternären Fall mit vertretbarem Aufwand zu ermitteln. Für Dreikomponentensysteme existieren eine Reihe von Näherungsformeln zur Vorhersage der Maxwell-Stefan-Diffusionskoeffizienten.^[6]

Ein großer Vorteil der Theorie ist, dass Systeme betrachtet werden können, in denen die „klassische“ Ficksche Diffusionstheorie versagt. So sind in der Maxwell-Stefan-Theorie beispielsweise auch negative Diffusionskoeffizienten nicht ausgeschlossen.

Es ist möglich, die Ficksche Theorie aus der Maxwell-Stefan-Theorie herzuleiten.^[4]

Literatur

• R. B. Bird, W. E. Stewart, E. N. Lightfoot: Transport Phenomena, 2nd Ed., John Wiley & Sons, Inc., 2007, ISBN 0-470-11539-4
• J. A. Wesselingh und R. Krishna. Mass transfer in Multicomponent Mixtures. Delft University Press, 2000, ISBN 90-407-2071-1.

Einzelnachweise

1. ↑ J. C. Maxwell: On the dynamical theory of gases, The Scientific Papers of J. C. Maxwell, 1965, 2, 26-78.
2. ↑ J. Stefan: Über das Gleichgewicht und Bewegung, insbesondere die Diffusion von Gemischen, Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften Wien, 2te Abteilung a, 1871, 63, 63-124.
3. ↑ E. L. Cussler: Diffusion - Mass Transfer in Fluid Systems, 2nd Ed., Cambridge University Press, 1997, ISBN 0-521-56477-8
4. ↑ ^{a b} P. J. A. M. Kerkhof, M. A. M. Geboers: Review – Analysis and extension of the theory of multicomponent fluid diffusion, Chem. Eng. Science, 2005, 60, 3129–3167
5. ↑ Y. Demirel: Diffusion, Nonequilibrium Thermodynamics, 2nd Ed., Elsevier Science B.V., Amsterdam, 2007, 319–362
6. ↑ ^{a b} S. Rehfeldt, J. Stichlmair: Measurement and calculation of multicomponent diffusion coefficients in liquids, Fluid Phase Equilibria, 2007, 256, 99–104