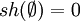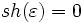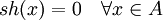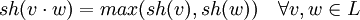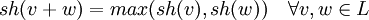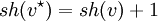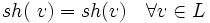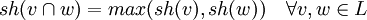Sternhöhenproblem

Die Sternhöhe ist ein Begriff aus der Theoretischen Informatik.

Definition

Die Sternhöhe sh(r) eines regulären Ausdrucks r über einem endlichen Alphabet A ist rekursiv definiert als

$sh(\emptyset) = 0$

$sh(\varepsilon) = 0$

$sh(x) = 0 \quad \forall x \in A$

$sh(v\cdot w) = max(sh(v),sh(w)) \quad\forall v,w \in L$

$sh(v+w) = max(sh(v),sh(w)) \quad\forall v,w \in L$

$sh(v^\star) = sh(v) + 1$

Darauf aufbauend ist die Sternhöhe sh(L) einer regulären Sprache L definiert als das Minimum aller Sternhöhen n für das ein regulärer Ausdruck r ∈ L mit sh(r) = n existiert.

Sternhöhenproblem

Das Sternhöhenproblem behandelt die Frage, ob es eine maximale Sternhöhe gibt, also ob ein n mit sh(L) <= n für alle regulären Sprachen L über einem festen Alphabet A existiert. Falls ein solches n nicht existiert, lässt sich dann die Sternhöhe einer regulären Sprache algorithmisch bestimmen?

Beide Fragen sind mittlerweile beantwortet. Im Jahre 1963 konnte L. C. Eggan zeigen, dass ein solches n nicht existiert, indem er für jedes n>=0 eine Sprache L_n mit sh(L) = n konstruierte. Kosaburo Hashiguchi stellte 1988 einen Algorithmus vor, mit dem sich zu einer gegebenen regulären Sprache L die Sternhöhe sh(L) bestimmen lässt.

Verallgemeinerte Sternhöhe

Die verallgemeinerte Sternhöhe gsh(r) ist analog zur Sternhöhe definiert, allerdings nicht über regulären Ausdrücken, sondern über verallgemeinerten regulären Ausdrücken. Es gilt also:

$sh(\emptyset) = 0$

$sh(\varepsilon) = 0$

$sh(x) = 0 \quad \forall x \in A$

$sh( ~ v) = sh(v) \quad \forall v \in L$

$sh(v\cdot w) = max(sh(v),sh(w)) \quad\forall v,w \in L$

$sh(v+w) = max(sh(v),sh(w)) \quad\forall v,w \in L$

$sh(v\cap w) = max(sh(v),sh(w)) \quad\forall v,w \in L$

$sh(v^\star) = sh(v) + 1$

Analog ist die verallgemeinerte Sternhöhe gsh(L) einer regulären Sprache L definiert.

Verallgemeinertes Sternhöhenproblem

Das verallgemeinerte Sternhöhenproblem ist analog zum Sternhöhenproblem definiert, aber im Gegensatz zu diesem noch unbeantwortet. Zwar gibt es reguläre Sprachen L mit gsh(L) = 1, zum Beispiel die Sprache 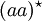$(aa)^\star$, offen ist aber noch die Frage, ob auch eine reguläre Sprache L mit gsh(L) >= 2 existiert.

Literatur

• L. C. Eggan, Transition graphs and the star-height of regular events, Michigan Math. J., 10(4): 385-397, 1963
• Kosaburo Hashiguchi, Algorithms for Determining Relative Star Height and Star Height, Inf. Comput. 78(2): 124-169, 1988
• Jean-Eric Pin, Howard Straubing and Denis Thérien, Some results on the generalized star-height problem, Information and Computation, 101(2):219-250, December 1992. http://www.liafa.jussieu.fr/~jep/Resumes/StarHeight.html