Stichbogen

Als Bogen bezeichnet man in der Architektur eine Konstruktion zum Überbrücken von Öffnungen in Mauerwerk.

Ein falscher Bogen oder Kragbogen ist die Erweiterung oder Verlängerung eines Balkens, der in der Antike als Kraggewölbe zur Konstruktion von Decken diente.

Ein echter Bogen vermeidet im Sinne einer Stützlinie Zugspannungen, die ein Stein nur unzureichend aufnehmen kann, und überträgt statt dessen Druckkräfte auf die seitlichen Lager. Er ist die zweidimensionale Variante eines echten Gewölbes. So ist das Tonnengewölbe ein sehr breiter Bogen. Echte Bögen sind bis zur Vollendung der Konstruktion nicht selbsttragend und benötigen ein Lehrgerüst.

Der Bogen ist in der Architektur an zahlreichen Bauwerken in unterschiedlichen Ausführungen zu finden. So ermöglicht der Bogen Brückenbauwerke, Tür- und Fensteröffnungen.

Bogentypen

Balken

Ein Balken, der eine Öffnung (Fenster, Tür, Tor) im Mauerwerk nach oben hin schließt, wird auf Biegung belastet: die Oberseite wird gestaucht, die Unterseite gedehnt. Während Holz hohe Zugspannungen aufnehmen kann, ist die Zugbelastung von Stein, erst recht von Mauerwerk, sehr gering. Steinbalken können nur kleine Öffnungen überbrücken. Sie wurden daher häufig durch einen zusätzlichen, darüber gemauerten Bogen entlastet (oft unsichtbar unter dem Putz liegend).

Kragbogen

Siehe Kragbogen

Schildbogen

Beim Schildbogen handelt es sich um einen Bogen über dem Obergadenfenster, welches typisch für die Basilika (frühchristlich, romanisch) ist.

Echter Bogen

Abgeschrägte Bausteine formen einen Bogen, der hohe Belastungen aufnehmen kann.

Lockeres Mauerwerk besitzt überhaupt keine Zugfestigkeit. Auch Mörtel ändert daran wenig. Seine Aufgabe ist es, die Auflage der Steine zu verbessern, nicht aber, die Steine zu verkleben. Hingegen ist die Druckfestigkeit außerordentlich hoch. Bei Zement liegt sie bei ca. 50 MN/m², ca. 10-fach höher als die Zugfestigkeit.

Balken und Kragbogen setzen Materialien voraus, die unter Zug belastbar sind. Erst eine Bogenkonstruktion nutzt die hohe Druckbelastbarkeit von mineralischen (Stein und Beton) und keramischen (Ziegel) Baustoffen.

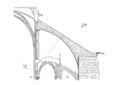
Die Steine in den beiden Bildern links sind keilförmig angeschrägt und lassen sich zu einem Bogen zusammen fügen. Nur die beiden "Pfosten" sind gegen seitliches Verschieben gesichert. Die Bogensteine selber sind nicht verklebt und können daher keine Zugkräfte aufnehmen. Die auf diese Weise lose aneinanderliegenden Steine vermögen dennoch hohe Belastungen als Druckspannungen aufzunehmen, die – im Gegensatz zu einem Kragbogen - ein Vielfaches des Eigengewichts betragen.

Elemente eines Bogens

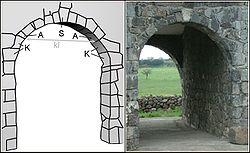
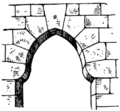
Die angeschrägten Bausteine nennt man Keilsteine. Der mittlere Stein im Bogen wird Schlussstein (S, siehe Bild rechts) genannt und ist häufig dekorativ herausgearbeitet. Von der Statik her unterscheidet er sich nicht von den anderen Steinen. Die Basis des Bogens heißt Kämpfer (K). Sie muss sorgfältig gearbeitet sein, damit die Druckkräfte an die Umgebung weitergeleitet werden können. Sie definiert die Kämpferlinie (kl). Oberhalb der Kämpferlinie beginnt der eigentliche Bogen. Die ersten Steine, die auf dem Kämpfer aufliegen, bezeichnet man als Anfänger (A). Die Bogenlaibung ist die Innenfläche des Bogens (in der Abbildung dunkelgrau schattiert), die Vorderfront die Bogenstirn. Die obere Fläche des Bogens, der Bogenrücken, trägt die nach oben aufgeschichteten Steine.

Ein sich nach unten öffnender Bogen, der die Kräfte gleichmäßig als Druckspannung aufnimmt, kann als Umkehrung einer frei hängenden Kette aufgefasst werden, in der ausschließlich Zugkräfte herrschen. Die Ideallinie eines unbelasteten Bogens ist deshalb eine Katenoide. Dennoch kommt ein Halbkreisbogen einer Brücke der Idealstruktur recht nahe, da der Bogen am Anfang und Ende wegen der Brückenrampe mehr Masse zu tragen hat als die Mitte.

Während sich die altgriechischen Stein-Monumentalbauten aus Tradition an Holzkonstruktionen orientierten, setzten die Römer durchgängig Halbrundbogen als tragende Strukturen ein (s.u.).

Bogenkonstruktionen

Im Laufe der Jahrhunderte wurden verschiedenste Arten von Bögen entwickelt, mit entsprechenden Vor- und Nachteilen.

Kragbogen

Maya-Bogen, Beispiel eines Kragbogens

Kragbogen

Das Bild zeigt einen typischen Maya-Bogen. Da echte Bögen unbekannt waren, konnten nur geringe Breiten überspannt werden, bei hohem Materialeinsatz zur Stabilisierung durch Gewicht.

Weitere Beispiele unter Kragbogen und Kraggewölbe.

Giebelbogen

Giebelbogen über einer Fensteröffnung

Der Giebelbogen, oder Dreiecksbogen, ist eine Bogenkonstruktion aus zwei schräg, in Giebelform, aneinandergelegten Steinen. Er wird insofern von zwei Geraden gebildet, erfüllt aber konstruktiv die Voraussetzungen eines Bogens. ^[1]

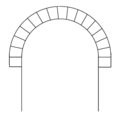
Halbkreisbogen oder Rundbogen

Alte römische Brücke.

Rundbogen

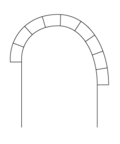
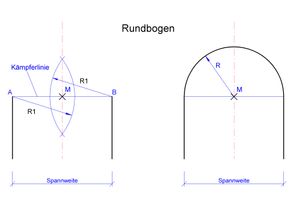
Beim Kreisbogen (auch Rundbogen) ist die Bogenlinie kreisförmig und nimmt den kompletten Halbkreis (180 Grad) ein, das bedeutet, die untersten beiden Fugen liegen horizontal. Die Höhe des Bogens (Scheitelhöhe) beträgt damit immer genau die halbe Spannweite. Der Halbkreisbogen war lange Zeit die dominierende Technik des Bogenbaus. Sie wurde von den Römern perfektioniert und vielfältig angewendet, was bis in die Zeit der Romanik wirkte.

Spitzbogen

Seitenwand mit Spitzbogen / Bolton Abbey

Spitzbögen von links nach rechts:
normaler Spitzbogen
gedrückter Spitzbogen
überhöhter Spitzbogen, bzw. Lanzettbogen

Der Spitzbogen ist ein aus zwei Kreisen konstruierter Bogen mit Spitze. Er gilt in der Architektur als ein zentrales Element der Gotik.

Erste Spitzbögen fanden sich bereits in der Burgundischen Romanik. In der gotischen Sakralarchitektur (Basilika Saint-Denis) wurden sie seit der ersten Hälfte des 12. Jahrhunderts verwendet. Von Frankreich aus verbreitete sich diese Bogenform um 1200 nach Deutschland, wurde bis in das frühe 16. Jahrhundert hinein benutzt und Jahrhunderte später, in der Neugotik, wieder aufgegriffen.

Tudorbogen

Tudorbogen an Francis Stuyvesant Peabody's Tudor Gothic mansion

Tudorbogen

Als Tudorbogen bezeichnet man in der Baukunst einen für den Tudorstil charakteristischen sehr flachen Spitzbogen. Er fand vor allem in England Verbreitung, weshalb er auch englischer Spitzbogen oder normannischer Bogen genannt wird. Er besteht aus vier Kreisbogen mit je zwei verschieden großen Radien.

Siehe auch: Haus Tudor

Segmentbogen

Segmentbogen aus Ziegel über einem Fenster

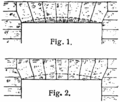
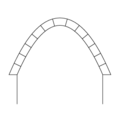
Segmentbogen

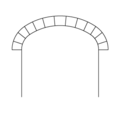
Ein Segmentbogen ist ein Kreisbogen, der keinen vollen Halbkreis beschreibt, sondern ein Kreissegment mit einem Winkel kleiner 180°. Der Segmentbogen ist damit flacher als ein Halbkreisbogen. Nachteilig ist allerdings der größere Seitenschub, den der Segmentbogen ausübt. Die flache Bauweise mit Segmentbogen ist besonders vorteilhaft für weit gespannte Bogenbrücken, bei denen der Seitenschub in das angrenzende Erdreich eingeleitet wird und die damit deutlich flacher gebaut werden können als Brücken mit Halbkreisbogen.

Korbbogen

Korbbogen an einer Durchfahrt

Korbbogen

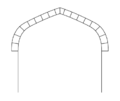
Der Korbbogen ist eine Weiterentwicklung des Segmentbogens, bei dem der Krümmungsradius im Bogenverlauf verändert wird. Die Krümmung verstärkt sich in Richtung Widerlager. Nach Anzahl der Mittelpunkte lässt sich der Bogen strecken. Bogen mit drei oder fünf Mittelpunkten sind die Regel^[2].

einhüftiger Korbbogen auch Schwanenhals

einhüftiger Korbbogen

Eine Sonderform des Korbbogens ist der einhüftige Korbbogen, auch Schwanenhals, steigender Bogen und Hüftbogen, genannt, bei dem die Kämpferpunkte in unterschiedlicher Höhe liegen. Dieser Bogentyp ist oft im Strebenwerk gotischer Kirchen zu finden. Auch für die tragende Unterkonstruktion von Treppen wird der einhüftige Korbbogen verwendet.

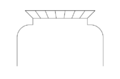
Scheitrechter Bogen

Scheitrechter Bogen als Entlastungsbogen über einem Fenstersturz. Antike Ruine in Perge.

Scheitrechter Bogen

Unechter scheitrechter Bogen (Durchgang zum Maschinenlabor der ETHZ)

Ein Scheitrechter Bogen, auch Horizontalbogen genannt, ist ein Bogen, der so ausgeführt ist, dass die überspannte Öffnung einem Balken gleicht. Konstruktiv ist es ein Segmentbogen, dessen Keilsteine so zugearbeitet sind, dass sich unten eine waagerechte Kante ergibt. Scheitrechte Bogen erlauben keine große Spannweite. Man findet sie häufig als Bogen über Fenster und Türen. Scheitrechte Bogen dienen oft als Entlastungsbogen über einen Fenstersturz aus Werkstein, auf dem nebenstehenden Foto ist dies zu erkennen. Man beachte den Zwischenraum zwischen Keilsteinen und Fenstersturz, der verhindert, dass der Fenstersturz statisch belastet wird. So hat das Bauteil ca. 1800 Jahre überlebt. Heute findet man sehr viele unechte scheitrechte Bogen an neuen Bauwerken die aber keine Bogenkonstruktionen sind sondern ihren Halt durch Verankerungen in den dahinterliegenden Stahlbetonstürzen haben. Oft sind sie leicht zu erkennen weil die Steine nicht radial angeordnet sind oder weil der mittlere Schlußstein wie auf dem Nebenstehenden Bild keine schrägen Seitenkanten aufweist oder gar verkehrt herum eingebaut wurde.

Hufeisenbogen

Hufeisenbogen

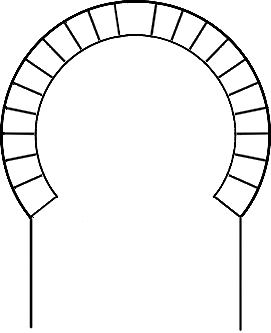
Hufeisenbogen

Hufeisenbogen haben ihren Namen von der hufeisenähnlichen Form. Die Bogenlänge beträgt zwischen 2/3 und 3/4 eines Kreisumfanges. Dieser Bogen ist in der islamischen Architektur vorherrschend und wird deshalb auch maurischer Bogen genannt. Dieser und viele andere architektonische Baustile gelangten durch die Mauren nach Europa. Allerdings verwendeten die Westgoten bereits den Hufeisenbogen in ihren Kirchenbauten bevor der Islam auf der iberischen Halbinsel Einzug hielt.

Vorhangbogen

Vorhangbogen

Der Vorhangbogen ist ein Bogen, der von konvexen Bogenlinien (auch mehreren) begrenzt wird.^[3]

Zackenbogen

Kleeblattbogen

Kleeblattbogen

Zackenbogen

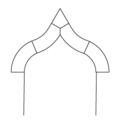
Dreipaßbogen

Der Zackenbogen ist eine gotische Bogenform, dessen Laibung aus Pässen und Nasen besteht. Die einfachste Form eines Zackenbogens ist der Kleeblattbogen oder auch Dreipassbogen. Der Kleeblattbogen setzt sich aus drei Kreisbogen zusammen, wobei der mittlere Kreisbogen größer sein kann. Es gibt auch spitze Kleeblattbogen, bei denen der mittlere Bogen ein Spitzbogen ist. Besteht ein Zackenbogen aus mehr als drei Bogen, so ist dies der eigentliche Zackenbogen, der auch Vielpassbogen oder Fächerbogen genannt wird.

Katenoide

Der Gateway Arch in St Louis ist eine Katenoide.

Die Katenoide entspricht genau dem Kräfteverlauf in einem dünnen Bogen. Ein Beispiel ist der Gateway Arch in St Louis. Der Bogenverlauf entspricht dem Durchhang einer Kette (Kettenlinie, Kettenkurve).

Parabelbogen

Parabelbogen

Parabelbogen

Aufgrund der geringen Abweichung von einer Katenoide werden Bogen manchmal auch als Parabel ausgeführt. Wenn der Bogen eine Last trägt, wie im Beispielbild links, flacht die Ideallinie ab. Sie ist weder eine Katenoide, noch eine Parabel, sondern nähert sich einem Halbkreis.

Karniesbogen

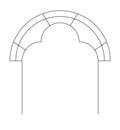
Karniesbogen

Karniesbogen

Kielbogen

Portal einer Kirche in Santa Isabel mit einem Kielbogen

Kielbogen

Ein Bogen, dessen Kante wie das Profil eines auf dem Rücken liegenden Schiffes mit Kiel aussieht, wird Kielbogen genannt. Andere Bezeichnungen dafür sind Eselsrücken – abgeleitet von der Rückenform eines Esels – und Sattelbogen

Schulterbogen

Schulterbogen über Portal

Schulterbogen

Der Schulterbogen ist eigentlich ein Kragbogen, dessen Sturzstützweite durch darunterliegende Kragsteine oder auch Konsolsteine verkürzt wurde. Andere Bezeichnungen sind daher Konsolbogen und Kragsturzbogen.

Schwibbogen

Schwibbögen in der via Botteghelle in Salerno

Der Schwibbogen ist ein Bogen, der zwei Gebäude spreizt. Der Bogen ist so übermauert, dass sich oben ein gerader Abschluss ergibt. Häufig findet sich der Schwibbogen in den engen Gassen mittelalterlicher Städte, z.B. Regensburg.

Strebebogen

Strebebogen am Straßburger Münster

Strebebogen am Notre Dame in Paris

Beim Strebebogen handelt es sich um einen asymmetrischer Bogen, der hoch aufragende Bauteile stützt. Er ist ein typisches Konstruktionsmerkmal an gotischen Basiliken als Teil des Strebewerkes.

• Überhöhter Bogen
• Umgekehrter Bogen
• Unechter Bogen

Elliptischer Bogen

Der Bogenverlauf folgt der Ellipse. Beide Brennpunkte liegen auf der Kämpferlinie^[2].

Einsatz von Bogen

• Brückenbogen: tragendes Element einer Brücke aus Stein, ist Grenzfall zu einem Tonnengewölbe.

• Chorbogen: Bogen zwischen Chor und Langhaus oder zwischen Chor und Vierung. Dieser Bogen wird auch Triumphbogen genannt.

Entlastungsbogen im Lexikon der gesamten Technik

• Entlastungsbogen: ein Bogen, der komplett im Mauerwerk liegt, um darunter liegende Teile zu entlasten und die Kräfte auf andere Bereiche zu verteilen. Sehr häufig über Fensterstürze aus Werkstein gemauert. Der verbleibende Zwischenraum zwischen Sturz und Entlastungsbogen ist nur lose vermauert.

• Gurtbogen: Stützt Tonnengewölbe oder trennt einzelne Felder eines Kreuzgewölbes ab und verbindet die tragenden Pfeiler.

• Mauerbogen: überspannt als Fenster- oder Torbogen eine Öffnung im Mauerwerk und trägt die Last des darüberliegenden Mauerwerks.

• Der Triumphbogen: ist ein monumentales Denkmal, das in Form eines freistehenden Bogens errichtet wird. Auch der Chorbogen wird Triumphbogen genannt.

Konstruktionsdetails

Folgende geometrische Konstruktionen werden für Bogen in der Praxis verwendet:

• Rundbogen

Die Kämpferlinie AB halbiert, ergibt den Punkt M, den Einsatzpunkt für das Zeichnen des Rundbogens mit R=Strecke AM bzw. BM.

Konstruktion Rundbogen

Konstruktion Stichbogen

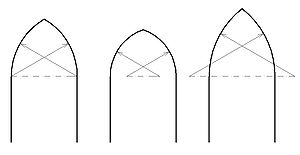
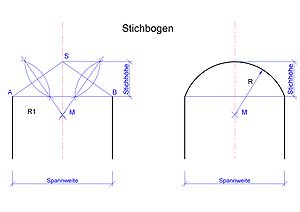
• Stichbogen

Auf der Kämpferlinie AB die Mittelsenkrechte errichten. Hierauf die Stichhöhe abtragen, ergibt den Scheitelpunkt S- Die Punkte A und B mit S verbinden. Die Mittelsenkrechten auf den Strecken AS und BS errichten. Sie schneiden sich im Punkt M. Punkt M ist der Einsatzpunkt für zum Zeichnen des Stichbogens.

• Gotischer Bogen

Mit der Spannweite um Punkt A und um Punkt B einen Kreisbogen mit Radius R=AB schlagen, ergibt den Scheitelpunkt S Die Verbindung der Punkte A, B, S ergeben ein gleichseitiges Dreieck.

Konstruktion Gotischer Bogen

Konstruktion gedrückter Gotischer Bogen

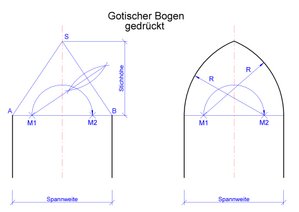
• Gotischer Bogen, gedrückt

Auf der Kämpferlinie AB eine Mittelsenkrechte errichten. Hierauf die Stichhöhe des Bogens abtragen, ergibt den Scheitelpunkt S. Die Stichhöhe muss wesentlich kleiner als die Spannweite, aber größer als die halbe Spannweite sein. Die Mittelsenkrechte auf der Strecke BS schneidet die Kämpferlinie und ergibt den Einsatzpunkt M1 zum zeichnen des Bogens mit R1. Durch Übertragen erhält man auf der anderen Seite den Einsatzpunkt M2.

• Korbbogen mit drei Einsatzpunkten
• Korbbogen mit fünf Einsatzpunkten

Gegeben ist die Strecke AB (Kämpferlinie) und die Scheitelhöhe C. Kreis um D mit dem Radius CD schlagen. Die sich ergebende Strecke A-E von D aus unter 45ø abtragen und unter Punkt D ein Quadrat mit den Punkten D_H_F_I errichten. Die Punkte F_I und F_H verlängern. Damit ergeben sich die Punkte J und K auf der Kämpferlinie. Einmal die Strecke D_F auf dem Mittellot nach unten abtragen. Es entsteht der Punkt G. Von Punkt G aus werden jeweils links und rechts ein Strahl durch den Punkt H und den Punkt I gezeichnet. Die Punkte G - H - I - J und K sind die Einstichpunkte für den Korbbogen !

Einzelnachweise

1. ↑ Absatz nach Hans Koepf, Günther Binding: Bildwörterbuch der Architektur, 4. Auflage, Stuttgart, Kröner, 2005. Die Synonymie zu Dreiecksbogen findet sich in der 4. Auflage nicht mehr, allerdings in der älteren 2. Auflage. In anderer Bedeutung wird unter Giebelbogen auch ein Ornament verstanden, so bei Günther Wasmuth (Hrsg.): Wasmuths Lexikon der Baukunst, Berlin, 1931, vgl. Giebel#Giebelschmuck
2. ↑ ^{a b} Tabellenbuch für das Bau- und Holzgewerbe, Ausgabe B, Wilhelm Friedrich, Fachbuchverlag GmbH Leipzig, 1951
3. ↑ Hans Koepf, Günther Binding: Bildwörterbuch der Architektur. Alfred Kröner, Stuttgart 1999.

Weblinks