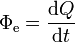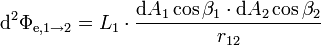- Strahlungsfluß
-
Physikalische Größe Name Strahlungsleistung Formelzeichen der Größe Φe Größen- und
Einheiten-
systemEinheit Dimension SI Watt (W) M·L2·T-3 Die Strahlungsleistung (auch Strahlungsfluss) ist die Strahlungsenergie dQ, die pro Zeiteinheit dt von elektromagnetischen Wellen transportiert wird:
Die Strahlungsleistung
Wird die Strahlungsleistung nur auf den sichtbaren Spektralbereich beschränkt, wird dieser oft als Lichtstrom (Einheit Lumen), das heißt die mit der V-Lambda-Kurve Vλ bewerteten Strahlungsleistung, bezeichnet.
Inhaltsverzeichnis
Fotometrische Grundgesetz
Um die Abhängigkeit der Strahlungsleistung
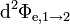 von einem Flächenelement dA1 einer Strahlerfläche A1 der Leuchtdichte L1 eines Lambert-Strahlers auf ein im Abstand r12 befindliches Flächenelement dA2 zu bestimmen, kann das sogenannte fotometrische Grundgesetz genutzt werden, das das lambertsche Kosinusgesetz und das fotometrische Entfernungsgesetz kombiniert.
von einem Flächenelement dA1 einer Strahlerfläche A1 der Leuchtdichte L1 eines Lambert-Strahlers auf ein im Abstand r12 befindliches Flächenelement dA2 zu bestimmen, kann das sogenannte fotometrische Grundgesetz genutzt werden, das das lambertsche Kosinusgesetz und das fotometrische Entfernungsgesetz kombiniert.Diese ist unter anderem abhängig von gegenseitigen Lage der beiden Flächen im Raum, dies wird durch die Winkeln β1 und β2 zwischen der Strahlrichtung und den Normalen der Flächenelemente beachtet.
Bezug zur Fotometrie
Fotometrische (also lichttechnische) Größen werden in der Regel durch das vorangestellte Wort Licht- bzw. Leucht- gekennzeichnet. Sie weisen die gleichen Formelzeichen wie die strahlungsphysikalischen Größen auf, beispielsweise Strahlungsleistung (strahlungsphysikalisch) und Lichtstrom (fotometrisch). Der Unterschied in der Kennzeichnung liegt im weglassen des Index „e“ bei fotometrischen Größen.
Der Index e bei Formelzeichen steht für eine energetische Messgröße, die eine objektive Messgröße ist; es fließen nicht die speziellen Eigenschaften der menschlichen Wahrnehmung ein (vgl. V-Lambda-Kurve). Im Gegensatz dazu wird der Index v bei Messgrößen gesetzt, bei denen die subjektiven Eigenschaften des menschlichen Auges einfließen, hier steht das v für visuell. Ein Beispiel wäre der Helligkeitsvergleich.
Siehe auch
Literatur
- F. Pedrotti, L. Pedrotti, W. Bausch, H. Schmidt: Optik für Ingenieure: Grundlagen. 2. Auflage. Springer, Berlin 2001, ISBN 3-540-67379-2.
Wikimedia Foundation.