- Streuspeicherung
-
Eine Hashfunktion oder Streuwertfunktion ist eine Funktion bzw. Abbildung, die zu einer Eingabe aus einer üblicherweise großen Quellmenge eine Ausgabe, den Hashcode, erzeugt, meist aus einer kleineren Zielmenge.
Die Hashwerte beziehungsweise Streuwerte sind meist skalare Werte aus einer Teilmenge der natürlichen Zahlen. Ein Hashwert wird auch als Fingerprint bezeichnet, da er eine nahezu eindeutige Kennzeichnung einer größeren Datenmenge darstellt, so wie ein Fingerabdruck einen Menschen nahezu eindeutig identifiziert.
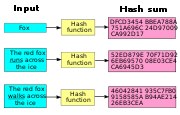 Beispiel einer Hashfunktion (hier SHA-1), links drei unterschiedliche Eingabewerte, rechts die entsprechenden Hashcodes
Beispiel einer Hashfunktion (hier SHA-1), links drei unterschiedliche Eingabewerte, rechts die entsprechenden HashcodesMit einem Hashcode werden z. B. Dokumente gekennzeichnet, um deren Authentizität beim Empfänger prüfbar zu machen, ohne den Inhalt des Dokuments selbst offenzulegen, etwa mittels der verbreiteten MD5-Funktion.
Hashfunktionen unterscheiden sich in der Definitionsmenge ihrer Eingaben, der Zielmenge der möglichen Ausgaben und im Einfluss von Mustern und Ähnlichkeiten verschiedener Eingaben auf die Ausgabe. Hashfunktionen werden in Hashtabellen, der Kryptologie und der Datenverarbeitung verwendet.
Hash-Algorithmen sind darauf optimiert, Kollisionen zu vermeiden. Eine Kollision tritt dann auf, wenn zwei verschiedenen Datenstrukturen derselbe Schlüssel zugeordnet wird. Da der Hashwert in der Praxis meist kürzer als die originale Datenstruktur ist, sind solche Kollisionen prinzipiell unvermeidlich, weshalb es Verfahren zur Kollisionserkennung geben muss. Eine gute Hashfunktion zeichnet sich dadurch aus, dass sie für die Eingaben, für die sie entworfen wurde, wenige Kollisionen erzeugt.
Der Name „Hashfunktion“ stammt vom englischen Verb to hash, das sich als „zerhacken“ übersetzen lässt. Der deutsche Name lautet Streuwertfunktion. Speziell in der Informatik verwendet man auch die Bezeichnung Hash-Algorithmus, da die Berechnung von Funktionen mittels Algorithmen durchgeführt wird.
Inhaltsverzeichnis
Anschauliche Erklärung
Bei einer Hashfunktion geht es meistens darum, zu einer Eingabe beliebiger Länge (zum Beispiel ein Text) eine kurze, möglichst eindeutige Identifikation fester Länge (den Hashwert des Textes) zu finden.
Das ist etwa dann sinnvoll, wenn man zwei große, ähnliche Dateien vergleichen will: Anstatt die 25 Seiten eines Textes durchzusehen, ob auch wirklich jeder Buchstabe gleich ist, ist anhand der kurzen Hashwerte der beiden Dokumente sofort zu sehen, ob diese (höchstwahrscheinlich) gleich oder (mit Sicherheit) verschieden sind.
Praktische Anwendung ist z. B. das Herunterladen einer Datei, zu der der Autor den Hashwert angegeben hat: Um zu prüfen, ob es Übertragungsfehler gegeben hat, braucht nicht die gesamte Datei ein zweites Mal heruntergeladen zu werden, sondern es muss nur der Hashwert gebildet und mit der Angabe des Autors verglichen werden.
Ein Beispiel für eine einfache Hashfunktion für Zahlen wäre, von der Zahl (Eingabe) die letzte Ziffer als Hashwert zu benutzen. Somit ergäbe 97 den Wert 7, 153 würde zu 3, selbst eine große Zahl wie 238.674.991 würde verkleinert zu 1. Der Wertebereich der unendlich großen Quellmenge würde also auf den Wertebereich von 0-9 abgebildet.
Weil bei einer Hashfunktion der Wertebereich meist kleiner als der der Quellmenge ist, können mehrere verschiedene Eingaben die gleiche Ausgabe erzeugen. Das leuchtet bei unserem Beispiel unmittelbar ein: 11 und 21 liefern beide 1. Das ist die Schwachstelle von Hashfunktionen und wird als Kollision bezeichnet. Durch die Wahl einer geeigneten Funktion kann die Wahrscheinlichkeit solcher Kollisionen deutlich vermindert werden, und man gewinnt für die praktische Anwendung eine hinreichende Sicherheit. Jedoch ist die Wahrscheinlichkeit für Kollisionen sehr groß, wenn schon einige Daten gespeichert wurden, vgl. auch Geburtstagsparadoxon. Man muss sich für den Fall einer Kollision somit auch immer eine Strategie der Kollisionsauflösung überlegen.
Eine weitere Schwachstelle der oben aufgeführten Beispielfunktion ist, dass nur die Änderung der letzten Stelle eine Änderung des Hashwertes ergibt; ein Zahlendreher außerhalb der letzten Ziffer oder eine fehlende Ziffer weiter vorn würde stets unentdeckt bleiben.
Anwendungen
Hashfunktionen haben verschiedene Anwendungsfelder. Dabei lassen sich drei große Gebiete unterteilen:
- Datenbanken
- Kryptologie
- Prüfsummen
Hashfunktionen in Datenbanken
Datenbankmanagementsysteme verwenden Hashfunktionen, um Daten in großen Datenbeständen mittels Hashtabellen zu suchen. In diesem Fall spricht man von einem Datenbankindex.
Kryptologie
In der Kryptologie werden kryptologische Hashfunktionen zum Signieren von Dokumenten oder zum Erzeugen von Einweg-Verschlüsselungen verwendet.
Hashwerte sind auch Bestandteil von verschiedenen Verschlüsselungsverfahren, wie beispielsweise dem Temporal Key Integrity Protocol (TKIP).
Prüfsummen
Prüfsummen werden verwendet um Änderungen an Daten zu erkennen, die entweder durch technische Störeinflüsse oder absichtliche Manipulation auftreten können.
Eine Manipulation ist feststellbar, wenn die berechnete Prüfsumme der geänderten Daten sich von der Prüfsumme der Originaldaten unterscheidet. Die Eignung verschiedener Hashfunktionen zur Prüfsummenberechnung hängt von der Kollisionswahrscheinlichkeit der berechneten Prüfsummen ab. Eine Kollisionsfreiheit ist nur möglich, wenn der Prüfsummenwertebereich größer gleich dem Wertebereich der Eingabedaten ist.
Wenn die Prüfsumme vor gezielten Manipulationen der Daten schützen soll, wird eine kryptographische Hashfunktion verwendet, welche unumkehrbar ist.
Beispiele
Hashwerte haben unter anderem bei P2P-Anwendungen aus verschiedenen Gründen eine wichtige Aufgabe. Die Hashwerte werden hier sowohl zum Suchen und Identifizieren von Dateien als auch zum Erkennen und Prüfen von getauschten Dateifragmenten verwendet. So lassen sich große Dateien zuverlässig in kleinen Segmenten austauschen.
Zur Anwendung in P2P-Netzen kommen vor allem gestufte Hashfunktionen, bei denen für kleinere Teile einer Datei der Hashwert und dann aus diesen Werten ein Gesamtwert berechnet wird. Bei den Netzwerken Gnutella G2, Shareaza und Direct Connect sind dies zum Beispiel Tiger-Tree-Hash-Funktionen.
Das Auffinden von Dateien aufgrund des Hashwertes ihres Inhaltes ist zumindest in den USA als Softwarepatent geschützt. Der Inhaber verfolgt Programme und Firmen, die auf Basis dieses Systems die Suche von Dateien ermöglichen, einschließlich Firmen, die im Auftrag von RIAA oder MPAA Anbieter von unlizenzierten Inhalten ermitteln wollen.
Bei der Programmierung von Internet-Anwendungen werden Hashfunktionen zum Erzeugen von Session-IDs genutzt, indem unter Verwendung von wechselnden Zustandswerten (wie Zeit, IP-Adresse) ein Hashwert berechnet wird.
Definition einer Hashfunktion
Eine Abbildung
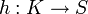 heißt Hashfunktion, wenn
heißt Hashfunktion, wenn 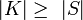 gilt. Insbesondere liefert h eine Hashtabelle der Größe | S | . S heißt auch die Menge der Schlüssel. Die Menge K repräsentiert die Daten, die gehasht werden sollen. Typischerweise wird die Menge der Schlüssel als Anfangsstück der natürlichen Zahlen gewählt:
gilt. Insbesondere liefert h eine Hashtabelle der Größe | S | . S heißt auch die Menge der Schlüssel. Die Menge K repräsentiert die Daten, die gehasht werden sollen. Typischerweise wird die Menge der Schlüssel als Anfangsstück der natürlichen Zahlen gewählt:  Diese Menge heißt dann auch Adressraum.
Diese Menge heißt dann auch Adressraum.Typischerweise wird in der Praxis immer nur eine kleine Teilmenge
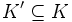 mit h abgebildet. Die Menge
mit h abgebildet. Die Menge 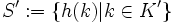 sind dann die tatsächlich genutzten Schlüssel.
sind dann die tatsächlich genutzten Schlüssel.Das Verhältnis
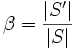 liefert uns den Belegungsfaktor.
liefert uns den Belegungsfaktor.Der Fall
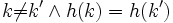 wird als Kollision bezeichnet. Eine injektive Hashfunktion heißt perfekt, u.a. weil sie keine Kollisionen erzeugt.
wird als Kollision bezeichnet. Eine injektive Hashfunktion heißt perfekt, u.a. weil sie keine Kollisionen erzeugt.Kriterien für eine gute Hashfunktion
- Geringe Wahrscheinlichkeit von Kollisionen der Hashwerte für den Eingabewertebereich bzw. möglichst Gleichverteilung der Hashwerte
- Datenreduktion – Der Speicherbedarf des Hashwertes soll deutlich kleiner sein als jener der Nachricht.
- Chaos – Ähnliche Quellelemente sollen zu völlig verschiedenen Hashwerten führen. Im Idealfall verändert das Umkippen eines Bits in der Eingabe durchschnittlich die Hälfte aller Bits im resultierenden Hashwert.
- Surjektivität – Kein Ergebniswert soll unmöglich sein, jedes Ergebnis (im definierten Wertebereich) soll tatsächlich vorkommen können.
- Effizienz – Die Funktion muss schnell berechenbar sein, ohne großen Speicherverbrauch auskommen und sollte die Quelldaten möglichst nur einmal lesen müssen.
Zusätzliche Forderungen für kryptographisch sichere Hashfunktionen
Eine kryptologische Hashfunktion sollte zumindest eine Einwegfunktion sein. Sogenannte Einweg-Hashfunktionen (One-Way-Hash Functions, OWHFs) erfüllen die Bedingung, eine Einwegfunktion zu sein, d. h. zu einem gegebenen Ausgabewert h(x) = y ist es praktisch unmöglich, einen Eingabewert x zu finden (engl. preimage resistance).
Außerdem ist eine Hashfunktion besser für die Kryptographie geeignet, wenn möglichst keine Kollisionen auftreten. Das heißt, dass für zwei verschiedene Werte x und x′ der Hashwert möglichst auch verschieden sein sollte: h(x)
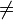 h(x′). Ist dies immer der Fall, so kann von einer kollisionsresistenten Hashfunktion (Collision Resistant Hash Function, CRHF) gesprochen werden.
h(x′). Ist dies immer der Fall, so kann von einer kollisionsresistenten Hashfunktion (Collision Resistant Hash Function, CRHF) gesprochen werden.Bekannte Hash-Berechnungsmethoden
- Divisions-Rest-Methode
- Doppel-Hashing
- Brent-Hashing
- Multiplikative Methode
- Mittquadratmethode
- Zerlegungsmethode
- Ziffernanalyse
- Quersumme
Allgemeine Hash-Algorithmen
- Adler-32
- FNV
- Hashtabelle
- Merkles Meta-Verfahren
- Modulo-Funktion
- Parität
- Prüfsumme
- Prüfziffer
- Quersumme
- Salted Hash
- Zyklische Redundanzprüfung
Hash-Algorithmen in der Kryptographie
Angriffe
Man unterscheidet Kollisionsangriffe und die wesentlich aufwändigeren Preimage-Angriffe. Bei einem Kollisionsangriff geht es darum, zwei beliebige Eingaben zu finden, die sich auf den gleichen Hashwert abbilden lassen. Bei einem Preimage-Angriff muss hingegen zu einer vorgegebenen Eingabe eine andere Eingabe mit gleichem Hashwert gefunden werden.
Literatur
- Donald E. Knuth: The Art of Computer Programming Volume 3. 2. Auflage. Addison Wesley, 1998, ISBN 0-201-89685-0, S. 513 ff..
- Cormen et. al.: Introduction to Algorithms. 2. Auflage. MIT Press, 2001, ISBN 0-262-03293-7, S. 229 ff..
Weblinks
Wikimedia Foundation.
