Subgradient method — Subgradient methods are algorithms for solving convex optimization problems. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods can be used with a non differentiable objective function. When the objective… … Wikipedia
subgradient — noun subderivative … Wiktionary
Convex optimization — Convex minimization, a subfield of optimization, studies the problem of minimizing convex functions over convex sets. Given a real vector space X together with a convex, real valued function defined on a convex subset of X, the problem is to find … Wikipedia
Subderivative — In mathematics, the concepts of subderivative, subgradient, and subdifferential arise in convex analysis, that is, in the study of convex functions, often in connection to convex optimization. Let f : I →R be a real valued convex function defined … Wikipedia
Naum Z. Shor — Naum Zuselevich Shor Born 1 January 1937(1937 01 01) Kiev, Ukraine, USSR Died 26 February 2006(2006 02 26 … Wikipedia
Mathematical optimization — For other uses, see Optimization (disambiguation). The maximum of a paraboloid (red dot) In mathematics, computational science, or management science, mathematical optimization (alternatively, optimization or mathematical programming) refers to… … Wikipedia
Ellipsoid method — The ellipsoid method is an algorithm for solving convex optimization problems. It was introduced by Naum Z. Shor, Arkady Nemirovsky, and David B. Yudin in 1972, and used by Leonid Khachiyan to prove the polynomial time solvability of linear… … Wikipedia
Newton's method — In numerical analysis, Newton s method (also known as the Newton–Raphson method), named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots (or zeroes) of a real valued function. The… … Wikipedia
Cutting-plane method — In mathematical optimization, the cutting plane method is an umbrella term for optimization methods which iteratively refine a feasible set or objective function by means of linear inequalities, termed cuts. Such procedures are popularly used to… … Wikipedia
Subdifferential — Das Subdifferential ist eine Verallgemeinerung des Gradienten. Inhaltsverzeichnis 1 Definition 2 Beispiel 3 Beschränktheit 3.1 Beweis … Deutsch Wikipedia
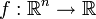 ist das Subdifferential im Punkt
ist das Subdifferential im Punkt 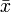 gegeben durch
gegeben durch für alle
für alle 
 heißen Subgradienten.
heißen Subgradienten. ist gegeben durch:
ist gegeben durch: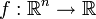 stetig und sei
stetig und sei 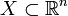 beschränkt. Dann ist die Menge
beschränkt. Dann ist die Menge  beschränkt.
beschränkt.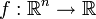 stetig und sei
stetig und sei 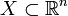 beschränkt. Setzte
beschränkt. Setzte  wobei
wobei  . Angenommen
. Angenommen  ist nicht beschränkt, dann gibt es für R: = 2ε ein
ist nicht beschränkt, dann gibt es für R: = 2ε ein  und ein
und ein  mit
mit  . Sei
. Sei  . Somit sind
. Somit sind  . Wir erhalten die Abschätzung
. Wir erhalten die Abschätzung .
.


![\partial f(\bar x)=\begin{cases}\{-1\} & \bar x<0\\
\left[-1,1\right] & \bar x=0\\ \{1\} & \bar x>0\end{cases}](/pictures/dewiki/54/631d68deb323b8894432e68f436712b1.png)