T-Konorm

Eine T-Norm, oft auch klein t-Norm, ist eine mathematische Funktion, die im Bereich mehrwertiger Logiken, insbesondere in der Fuzzy-Logik, Bedeutung erlangt hat. Der Begriff leitet sich vom Englischen triangular norm, zu Deutsch Dreiecksnorm ab, und rührt daher, dass eine T-Norm eine dreiecksähnliche Fläche in $\mathbb{R}^3$ beschreibt.

Eine T-Norm ist auf dem Einheitsintervall [0,1] definiert

$T : [0,1] \times [0,1] \rightarrow [0,1]$

und muss folgende Eigenschaften aufweisen (zur exakten Definition dieser Eigenschaften siehe die Tabelle zu T-Norm und T-Conorm am Ende dieses Artikels):

• Assoziativität: T(a, T(b, c)) = T(T(a, b), c)
• Kommutativität: T(a, b) = T(b, a)
• Monotonie: T(a, b) ≤ T(c, d), falls a ≤ c und b ≤ d
• 1 ist neutrales Element: T(a, 1) = a

Der Hintergrund bei der Entwicklung der T-Norm bestand darin, dass man für mehrwertige Logiken einen verallgemeinerten Konjunktions-Operator benötigte. Die oben genannten Eigenschaften sind gleichsam allgemeinste Eigenschaften eines solchen Operators: Assoziativität und Kommutativität sind selbstverständlich. Die Monotonie garantiert eine gewisse Regelmäßigkeit in der Struktur von Definitions- und Zielmenge. Die 1 als neutrales Element ermöglicht Konjunktionen, deren Ergebnis nur von einem Operanden abhängt.

Diese Eigenschaften werden im Zusammenhang mit Fuzzy-Mengen verwendet, um die Schnittmengen-Operation nachzubilden.

Komplementär zu T-Normen werden T-Conormen (od. auch S-Normen) verwendet. Mit Hilfe der de Morganschen Gesetze lässt sich nämlich auf der Basis einer T-Norm, welche Konjunktion bzw. Schnittmenge liefert, und einer Negation die Disjunktions- bzw. die Vereinigungsmengen-Operation ableiten.

Geläufige T-Normen und T-Conormen

$\begin{matrix} \mathrm{\top_{min}}(a, b) &=& \min \{a, b\} & \mathrm{\bot_{max}}(a, b) &=& \max \{a, b\} \\ \\ \mathrm{\top_{Luka}}(a, b) &=& \max \{0, a+b-1\} & \mathrm{\bot_{Luka}}(a, b) &=& \min \{a+b, 1\} \\ \\ \mathrm{\top_{prod}}(a, b) &=& a \cdot b & \mathrm{\bot_{sum}}(a, b) &=& a+b- a \cdot b \\ \\ \mathrm{\top_{-1}}(a, b) &=& \left\{\begin{matrix}a, & \mbox{falls }b=1 \\ b, & \mbox{falls }a=1 \\ 0, & \mbox{sonst}\end{matrix} \right. & \mathrm{\bot_{-1}}(a, b) &=& \left\{\begin{matrix}a, & \mbox{falls }b=0 \\ b, & \mbox{falls }a=0 \\ 1, & \mbox{sonst}\end{matrix}\right. \end{matrix}$

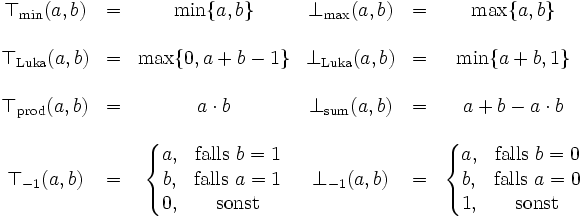
Die angegebenen T-Conormen sind jeweils bezüglich der Standardnegation N(x)=1-x zur entsprechenden T-Norm dual, also über die de Morganschen Gesetze verknüpft. Mit anderen involutiven Negationen ergeben sich im Allgemeinen auch andere T-Conormen.

Die erstgenannte wird wegen ihrer Einfachheit und ihrer unten genannten Eigenschaften am häufigsten eingesetzt. Die 3. T-Norm, sowie deren T-Conorm kommen aus der Wahrscheinlichkeitrechnung. Weiterhin gelten folgende Zusammenhänge:

$\begin{matrix} \mathrm{\top_{-1}}(a, b) & \le & \top(a, b) & \le & \mathrm{\top_{min}}(a, b) \\ \mathrm{\bot_{max}}(a, b) & \le & \bot(a, b) & \le & \mathrm{\bot_{-1}}(a, b) \end{matrix}$
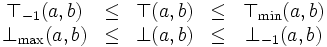
D.h. dass die drastische T-Norm (T_-1) die kleinste und die Minimum-T-Norm die größte ist. Umgekehrtes gilt für die T-Conorm. T(a, b) bzw. ⊥(a, b) steht hierbei für jede beliebige T-Norm bzw. T-Conorm.

Zusammenhänge zwischen T-Norm und T-Conorm

Aufgrund der schon erwähnten De Morganschen Gesetze ergeben sich folgende Zusammenhänge:

1-⊥(a,b) = T(1-a, 1-b)

1-T(a,b) = ⊥(1-a, 1-b)

Folgende Bedingungen werden verlangt, damit eine Funktion als T-Norm bzw. T-Conorm gilt:

	T-Norm	T-Conorm
Nullelement:	T(0,a) = T(a,0) = 0	⊥(a,1) = ⊥(1,a) = 1
Neutrales Element:	T(a,1) = T(1,a) = a	⊥(0,a) = ⊥(a,0) = a
Assoziativität:	T(a,T(b,c)) = T(T(a,b),c)	⊥(a,⊥(b,c)) = ⊥(⊥(a,b),c)
Kommutativität:	T(a,b) = T(b,a)	⊥(a,b) = ⊥(b,a)
Monotonie:	a ≤ b ⇒ T(a,c) ≤ T(b,c)	a ≤ b ⇒ ⊥(a,c) ≤ ⊥(b,c)