- Telegrafengleichung
-
Dieser Artikel befasst sich mit der Telegraphengleichung der Elektrodynamik. Die (speziellere) Telegraphengleichung der Elektronik wird unter Telegraphengleichung (Elektronik) behandelt. 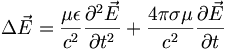
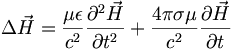 .
.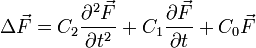 .
.- Adolf J. Schwab: Begriffswelt der Feldtheorie, Springer Verlag, ISBN 3-540-42018-5
Die Telegraphengleichung ist eine allgemeine Form der Wellengleichung. Sie wurde wahrscheinlich zum ersten Mal von William Thomson, 1. Baron Kelvin bei der Berechnung der Fortpflanzung von Telegraphiesignalen auf Seekabeln aufgestellt.
Mit den Materialgleichungen kann man die Maxwellgleichungen in ladungsfreien Raumgebieten umschreiben zu
und
Im Fall eines Isolators ist σ = 0 und die Maxwellgleichungen reduzieren sich zur (vektoriellen) Wellengleichung.
Jede dieser Gleichungen ist eine spezielle Form der Telegraphengleichung. Diese ist eine partielle Differentialgleichung (wenn C2 > 0 hyperbolisch, bei < 0 elliptisch und = 0 parabolisch) und lautet in der allgemeinen Form
In dieser Form ist sie eine Gleichung, die viele andere lineare partielle Differenzialgleichungen der Physik als Spezialfälle enthält (Wellengleichung, Diffusionsgleichung, Helmholtz-Gleichung, Potenzialgleichung) und entsprechend ist sie auch allgemein behandelbar.
Inhaltsverzeichnis |
Telegraphengleichung mit a,b>0; c=0
Die Gleichungen sind allgemein vom Typ:
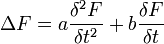
Ersetzt man beispielsweise F durch E oder H und wählt a=εμ sowie b=σμ erhält man die Wellengleichung für ein verlustbehaftetes Dielektrikum.
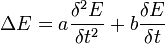
bzw.
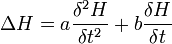
Telegraphengleichung mit a>0; b=0; c=0
Die Gleichungen sind allgemein vom Typ:
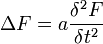
Und tragen oberbegrifflich den Namen Wellengleichung. Ersetzt man beispielsweise F durch E oder H und wählt a=εμ, erhält man die Wellengleichungen elektromagnetischer Wellen im verlustfreien Raum.
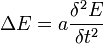
bzw.
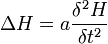
Ersetzt man F durch u oder durch i, so erhält man die Wellengleichung für die Ausbreitung von Spannungs- und Stromwellen längs verlustfreier Leitungen:
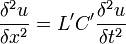
bzw.
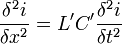
Ersetzt man F durch die Auslenkung L von Masseteilchen und a durch den Kehrwert der Wellenausbreitungsgeschwindigkeit v, erhält man die Wellengleichung mechanischer Wellen:
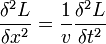
Telegraphengleichung mit a=0; b>0; c=0
Die Gleichungen sind allgemein vom Typ:
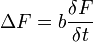
und tragen oberbegrifflich den Namen Wärmeleitungsgleichung oder Diffusionsgleichung. Ersetzt man F durch E, H oder JL und wählt b=σμ, erhält man die Gleichungen für das Strömungsfeld in Leitern mit Stromverdrängung:
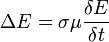
bzw.
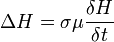
bzw.
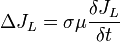
Ersetzt man F durch die Temperatur T und b durch Cρ/λ (C spezifische Wärme, ρ Dichte, λ Wärmeleitfähigkeit), so erhält man die partiellen Differentialgleichungen für räumlich-zeitliche Temperaturverteilungen:
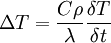
Quelle
Wikimedia Foundation.
