Temporal Logic of Actions

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Die Temporale Logik der Aktionen (TLA) ist eine Weiterentwicklung der Temporalen Logik (engl. temporal logic) und der Logik der Aktionen (engl. logic of actions). Sie wurde von Leslie Lamport entwickelt.

Die Temporale Logik der Aktionen gehört zur Aussagenlogik (engl. propositional logic) und wird in der Informatik zur Spezifikation, Argumentation und Verfikation von Systemen (z. B. Programmen) verwendet. Eine Spezifikation in TLA ist eine logische Formel, die alle möglichen und korrekten Verhalten eines Systems beschreibt. Anhand dieser logischen Formel können Systeme auf unerwünschte und gewünschte Eigenschaften geprüft werden.

Symbole

Es gelten die Symbole der booleschen Algebra und weitere Symbole

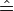
$\hat =$	gleich per Definition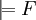
$\models F$	F ist gültig
$\Box$	immer
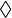
$\Diamond$	endlich, schließlich
$\circ$	zum nächsten Zeitpunkt
[A]	Aktion ( Stotterschritt )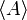
$\langle A \rangle$	Aktion

Syntax und Semantik

$\langle Formel \rangle$	$\hat =$	$\langle Formel \rangle \land \langle Formel \rangle$ $\vert$ $\langle Formel \rangle \lor \langle Formel \rangle$ $\vert$ $\neg \langle Formel \rangle$ $\vert$ $\Box \langle Formel \rangle$ $\vert$ $\Diamond \langle Formel \rangle$ $\vert$ $\langle Pr\ddot adikat \rangle$ $\vert$ $\Box {\lbrack \langle Aktion \rangle \rbrack}_{\langle Zustandsfunktion \rangle}$
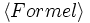
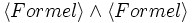
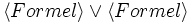
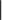
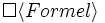
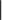
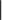
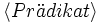
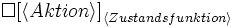
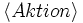
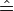
$\langle Aktion \rangle$	$\hat =$	boolescher Ausdruck aus Konstanten, Variablen und gestrichenen (engl. primed) Variablen. Eine Aktion stellt dabei eine Relation zwischen zwei Zuständen dar, wobei gestrichene Variablen sich auf den neuen Zustand beziehen. Ein Paar von Zuständen die eine Aktion A erfüllen wird A step genannt.
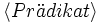
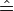
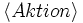$\langle Pr\ddot adikat \rangle$	$\hat =$	$\langle Aktion \rangle$ ohne gestrichenen Variablen  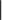 $\vert$  Enabled(Aktion)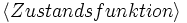
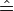
$\langle Zustandsfunktion \rangle$	$\hat =$	nichtboolescher Ausdruck aus Konstanten, Variablen zur Beschreibung eines Zustandes
Verhalten	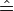$\hat =$	unendliche Sequenz von Zuständen

Im folgenden sind z,u Zustände, f Zustandsfunktionen, A Aktionen, F,G Formeln, p Prädikate, v Variablen und σ Verhalten.

Sei f eine Zustandsfunktion oder ein Prädikat, f' ist dann der Ausdruck f, in dem alle Variablen durch gestrichene Variablen ersetzt wurden.

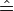
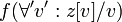
z[f]	$\hat =$	$f( \forall 'v' : z\lbrack v \rbrack /v )$
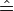
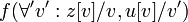
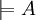
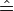
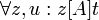
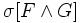
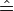
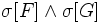
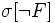
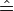
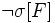
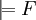
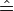
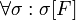
s[f]u	$\hat =$	$f( \forall 'v' : z\lbrack v \rbrack / v, u\lbrack v \rbrack /v' )$
$\models A$	$\hat =$	$\forall z,u : z \lbrack A \rbrack t$
$\sigma \lbrack F \land G \rbrack$	$\hat =$	$\sigma \lbrack F \rbrack \land \sigma \lbrack G \rbrack$
$\sigma \lbrack \neg F \rbrack$	$\hat =$	$\neg \sigma \lbrack F \rbrack$
$\models F$	$\hat =$	$\forall \sigma : \sigma \lbrack F \rbrack$
[A]f	$\hat =$	$A \lor ( f' = f )$
${\langle A \rangle}_f$	$\hat =$	$A \land ( f' \neq f )$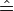

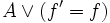
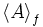
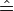
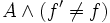
[A]_f ist ein Stotterschritt der den Wert der Variablen unverändert lässt (engl. stuttering step).

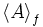${\langle A \rangle}_f$ ist ein Schritt der die Zustandsfunktion verändert.

Für jede Aktion A ist ein Prädikat Enabled A definiert. Es ist in einen Zustand nur dann true , wenn es möglich ist von diesem Zustand aus einen A step auszuführen. d.h. Enabled A ist im Zustand z true , falls ein Zustand u existiert, so dass 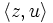$\langle z,u \rangle$ ein A step ist. In einem Verhalten ist ein Prädikat nur dann true wenn es in dem ersten Zustand true ist.

Verhaltenseigenschaften

Eine Sicherheitseigenschaft garantiert, dass unerwünschte Zustände niemals erreicht werden.

Eine Lebendigkeitseigenschaft garantiert, dass erwünschte Zustände erreicht werden.

In einem nebenläufigen System unterscheidet man zwischen schwacher und starker Fairness. Schwache Fairness (engl. weak fairness, justice) bedeutet, dass eine Aktion unendlich oft ausgeführt werden muss, wenn die Ausführung dieser ab einem bestimmten Zeitpunkt immer möglich ist. Anders: Wird eine Aktion nur endlich oft ausgeführt, so ist diese in einem Verhalten unendlich oft nicht ausführbar. Sie sichert zu, dass die Aktion schließlich ausgeführt wird oder, dass dessen Ausführung unmöglich wird – wenn auch nur für eine bestimmte Zeitspanne.

Starke Fairness (engl. strong fairness, compassion) bedeutet, dass eine Aktion unendlich oft ausgeführt werden muss, wenn die Ausführung dieser unendlich oft möglich ist. Anders: Wird eine Aktion nur endlich oft ausgeführt, so ist diese in einem Verhalten nur endlich oft ausführbar. Es versichert, dass die Aktion schließlich ausgeführt wird oder, dass dessen Ausführung schließlich für immer unmöglich wird.

Ist ein Verhalten stark Fair bezüglicher einer Aktion, so ist es auch schwach fair für diese Aktion.

Darstellung und Beispiel

var x=0, y=0

doParallel({x:=x+1},{y:=y+1})

Oben stehendes Program in Pseudocode soll in paralleler Verarbeitung (nichtdeterministisch) entweder zu x oder y 1 addieren.

Um eine TLA - Spezifikation angeben zu können, müssen erst die Zustandsfunktionen und Aktionen definiert werden.

In diesem Beispiel reicht ein Zustand, der gleichzeitig der Anfangszustand ist.

$Init_\phi = (x=0) \land (y=0)$

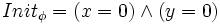
Die parallel ablaufenden Additionen können in zwei Aktionen M₁,M₂ beschrieben werden.

$M_1 \hat = (x'=x+1) \land (y'=y),$
$M_2 \hat = (y'=y+1) \land (x'=x),$
$M = M_1 \lor M_2$

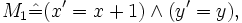
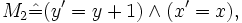
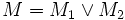
Zum Schluss werden noch Fairnessbedingungen spezifiziert. SF als starke Fairness und WF als schwache Fairness.

$SF_{\langle x,y \rangle} (M_1)$
$SF_{\langle x,y \rangle} (M_2)$

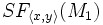
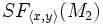
Aus diesen drei Bestandteilen erhalten wir folgende TLA-Formel:

$Init_\phi = (x=0) \land (y=0)$
$M_1 \hat = (x'=x+1) \land (y'=y) M_2 \hat = (y'=y+1) \land (x'=x)$
$M = M_1 \lor M_2$
$\phi \hat = Init_\phi \land \Box {\lbrack M \rbrack}_{\langle x,y \rangle} \land SF_{\langle x,y \rangle} (M_1) \land SF_{\langle x,y \rangle} (M_2)$

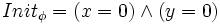
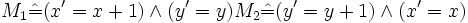
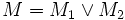
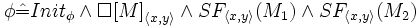
Siehe auch

• Formale Systeme
• Formale Semantik
• Formale Sprache
• Mobile Temporale Logik der Aktionen

Weblinks

• Temporal logic guide ( englisch )
• TLA – The Temporal Logic of Actions von Leslie Lamport ( englisch )