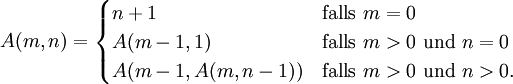Terminierender Algorithmus

Terminiertheit (auch: Terminierung, Termination) ist ein Begriff aus der Berechenbarkeitstheorie, einem Teilgebiet der theoretischen Informatik. Man sagt, ein Algorithmus terminiert (hält) für die Eingabe a, wenn er für die Eingabe a nach endlich vielen Arbeitsschritten zu einem Ende kommt, so dass die Berechnung in endlicher Zeit abgeschlossen wird. Man sagt, der Algorithmus terminiert (überall) oder ist terminierend, wenn er für jede Eingabe terminiert. Dabei wird keine für alle Eingaben gemeinsam gültige Obergrenze für die Anzahl der ausgeführten Arbeitsschritte gefordert.

Beispielsweise wächst die Anzahl zur Berechnung der Ackermannfunktion notwendigen Arbeitsschritte unbeschränkt für wachsende Eingabeparameter. Gleichwohl kann man zeigen, dass der entsprechende rekursive Algorithmus

$A(m, n) = \begin{cases} n+1 & \mbox{falls } m = 0 \\ A(m-1, 1) & \mbox{falls } m > 0 \mbox{ und } n = 0 \\ A(m-1, A(m, n-1)) & \mbox{falls } m > 0 \mbox{ und } n > 0. \end{cases}$

für alle Eingabewertpaare (m,n) terminiert.

Eine wichtige Aufgabe der Verifikation eines Computerprogramms (dem Beweis der Korrektheit) ist es, zu zeigen, dass das vorliegende Programm für gewisse Eingaben terminiert. Die Unentscheidbarkeit des Halteproblems besagt, dass es keinen Algorithmus gibt, der zu einem Paar (Programm, Eingabe) immer zutreffend sagen kann, ob das Programm für die Eingabe terminiert. Auch die Frage, ob ein Programm überall terminiert, ist unentscheidbar, das heißt nicht durch einen Algorithmus beantwortbar (Unentscheidbarkeit des Gleichmäßigen Halteproblems, engl. uniform halting problem).

Dass ein Algorithmus für eine Eingabe a unendlich lange rechnet, also für a nicht terminiert, weist man dadurch nach, dass man die unendliche Berechnung für a angibt. Oft ergibt sich dabei ein leicht zu erkennendes Muster, sodass man diese Berechnung endlich darstellen kann.

Für viele praktische Algorithmen ist deren Terminierung einfach zu zeigen (Terminierungsbeweis). Es gibt aber auch Probleme wie zum Beispiel das Collatz-Problem, die man als Fragen nach Terminierung verstehen kann, und für die bis jetzt keine Antwort gefunden wurde.

Siehe auch

• Determinismus (Algorithmus)
• Determiniertheit (Algorithmus)