Teststärke

Power (englisch für Kraft, Macht, Energie) oder Teststärke beschreibt in der Statistik die Aussagekraft eines statistischen Tests oder auch einer medizinischen Studie.

Die Teststärke gibt an, mit welcher Wahrscheinlichkeit ein Signifikanztest zugunsten einer spezifischen Alternativhypothese H₁ (z. B. „Es gibt einen Unterschied“) entscheidet, falls diese richtig ist. (Die abzulehnende Hypothese wird H₀, die Nullhypothese genannt.)

Die Teststärke hat den Wert 1-β, wobei β die Wahrscheinlichkeit bezeichnet, einen Fehler 2. Art zu begehen.

Entscheidungstabelle

	Wahrer Sachverhalt: H0 (Es gibt keinen Unterschied)	Wahrer Sachverhalt: H1 (Es gibt einen Unterschied)
durch einen statistischen Test fällt eine Entscheidung für: H0	richtige Entscheidung (Spezifität)	Fehler 2. Art Wahrscheinlichkeit: β
durch einen statistischen Test fällt eine Entscheidung für: H1	Fehler 1. Art Wahrscheinlichkeit: α	richtige Entscheidung Wahrscheinlichkeit: 1-β ("Power", Sensitivität)

Wahl des β-Fehler-Niveaus

Für Wirksamkeitsstudien medizinischer Behandlungen schlägt Cohen (1969) für β einen 4-mal so hohen Wert vor wie für das Signifikanzniveau α. Wenn α = 5% ist, sollte das β-Fehler-Niveau also 20 % betragen. Liegt in einer Untersuchung die β-Fehler-Wahrscheinlichkeit (Wahrscheinlichkeit für einen Fehler 2. Art) unter dieser 20 %-Grenze, so ist die Teststärke (1-β) damit größer als 80 %.

Es sollte dabei bedacht werden, dass der β-Fehler bei vorgegebenem, festem Signifikanzniveau α im Allgemeinen nicht direkt kontrolliert werden kann. Bei vielen asymptotischen oder nichtparametrischen Tests ist der β-Fehler unberechenbar oder es existieren lediglich Simulationsstudien. Bei einigen Tests, z.B. dem t-Test, kann der β-Fehler kontrolliert werden, wenn der statistischen Auswertung eine Fallzahlplanung vorausgeht.

Determinanten der Power

Die Power (1-β) wird größer ^[1]:

• mit wachsender Differenz von μ₀ − μ₁ (das bedeutet: ein großer Unterschied zwischen zwei Teilpopulationen wird seltener übersehen als ein kleiner Unterschied)
• mit kleiner werdender Merkmalsstreuung σ
• mit größer werdendem Signifikanzniveau α (sofern β nicht festgelegt ist)
• mit wachsendem Stichprobenumfang (da der Standardfehler dann kleiner wird: $\sigma_{\overline{x}} = \frac{\sigma}{\sqrt{n}}$)

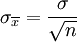Siehe auch

• Operationscharakteristik

Wichtig für die Power ist auch die Art des statistischen Tests: Parametrische Tests (z.B. t-Test) haben, falls die Verteilungsannahme stimmt, bei gleichem Stichprobenumfang stets eine höhere Power als nichtparametische Tests wie z.B. der Wilcoxon-Vorzeichen-Rang-Test. Weichen die angenommene Verteilung und die wahre Verteilung jedoch voneinander ab, liegt also z.B. in Wahrheit eine Laplace-Verteilung zugrunde, während eine Normalverteilungsannhame getroffen wurde, so können nichtparametrische Verfahren eine wesentlich größere Power als ihre parametrischen Gegenstücke besitzen.

Literatur

• Cohen, J.: Statistical Power Analysis for the Behavior Science. Erlbaum; Hillsdale, NJ 1969, ISBN 0-8058-0283-5

Weblinks

• G*Power 3 – frei verfügbares Programm zur Teststärkeanalyse

• [1] - Animation zum Fehler 1. und 2. Art

Quellen

1. ↑ Bortz, J.: Statistik für Sozialwissenschaftler. Springer, Berlin 1999. ISBN 3-540-21271-X