Bandtheorie

Das Bändermodell oder Energiebändermodell ist ein quantenmechanisches Modell zur Beschreibung von elektronischen Energiezuständen in einem idealen Einkristall, bei dem die Atomrümpfe in einem strengen periodischen Gitter vorliegen. Es gibt mehrere Energiebereiche, in denen viele quantenphysikalisch mögliche Zustände existieren, die energetisch so dicht liegen, dass sie als Kontinuum – als Energieband – angesehen werden können. Die zugehörige Darstellung wird als Banddiagramm bezeichnet.

Entstehung der Bänder

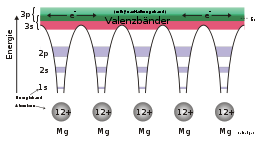
Betrachtet man ein einzelnes Atom, liegen die Energieniveaus des Atoms in diskreter Form vor. Dies gilt auch für weit voneinander entfernte Atome. Nähert man zwei Atome einander an, so wirkt das ähnlich wie bei gekoppelten Pendeln, wo sich die Anzahl der möglichen Schwingungsfrequenzen erhöht. Bei Atomen im Gitter spalten sich bei der Annäherung ab einem gewissen Abstand die atomaren Elektronenniveaus aufgrund der elektrostatischen Wechselwirkung der Elektronen (dem entspricht die Koppelfeder der gekoppelten Pendel) der beiden Atome auf. Die Energieniveaus verschieben sich jeweils leicht nach oben und unten. Betrachtet man nun einen Kristall, bei dem eine Vielzahl von Atomen miteinander wechselwirken, steigt die Anzahl der erlaubten Energiezustände entsprechend, sie verschmieren zu Energiebändern.

Die Breite der Energiebänder ist für die unterschiedlichen atomaren Energieniveaus nicht gleich. Der Grund dafür ist die unterschiedlich starke Bindung der Elektronen an ihr Atom. Elektronen auf niedrigen Energieniveaus sind stärker gebunden und wechselwirken weniger mit Nachbaratomen. Dies führt zu schmalen Bändern. Die Valenzelektronen im Valenzband (bei Metallen gleich dem Leitungsband) sind leichter gebunden und können daher die Potentialberge zwischen den Atomen einfacher überwinden. Sie wechselwirken stark mit denen der Nachbaratome und lassen sich in einem Kristall nicht mehr einem einzelnen Atom zuordnen, diese Bänder werden dabei breiter, siehe Abbildung.

Bändermodell mit Potentialtöpfen am Beispiel des Metalls Magnesium

Siehe auch: Modell der quasifreien Elektronen

Grundlagen für den Leitungsvorgang von elektrischen Ladungen

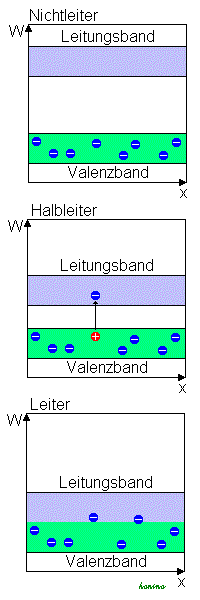
Bei der Betrachtung der elektronischen Eigenschaften eines Kristalls sind vor allem das Valenz- und das Leitungsband von Bedeutung. Am absoluten Nullpunkt (Temperatur) ist das Valenzband das höchste vollständig besetzte Energieband. Das energetisch darüberliegende, unbesetzte oder teilweise besetzte Band nennt man Leitungsband. Bei Halbleitern und Isolatoren liegt zwischen beiden Bändern ein verbotener Bereich, der Bandlücke genannt wird. Das Ferminiveau gibt an, bis zu welcher Energie Zustände (am absoluten Nullpunkt, T = 0 K) besetzt sind.

Die Leitfähigkeit des Kristalls hängt zum einen davon ab, ob das Leitungsband am Nullpunkt besetzt, teilweise besetzt oder unbesetzt ist, und zum anderen davon welche Temperatur er besitzt. Ein voll besetztes Band trägt, genau wie ein unbesetztes Band, nicht zum Ladungstransport bei. Die Ursache dafür ist, dass Elektronen in voll besetzten Bändern keine Energie, z. B. durch ein elektrisches Feld, aufnehmen können, denn es gibt für sie keine unbesetzten Zustände mit etwas höherer Energie. Erst ein teilbesetztes Band ermöglicht im elektrischen Feld einen von Null verschiedenen Nettostrom.

Wie oben beschrieben, besitzen Halbleiter und Isolatoren eine Bandlücke. Da ihre Valenzbänder bei 0 K voll besetzt sind, ist kein Ladungstransport möglich. Führt man dem Material durch Temperaturerhöhung oder Lichteinstrahlung ausreichend Energie zu, können Elektronen die Bandlücke überwinden und ins Leitungsband angehoben werden. Auf diese Weise kann ein unbesetztes Leitungsband teilbesetzt werden. Diese Elektronen und die im Valenzband zurückbleibenden Löcher tragen beide zum elektrischen Strom bei (Eigenleitung).

Einteilung anhand der Lage der Bänder

Energiebänder in Nichtleiter, Halbleiter und Leiter

Isolatoren

Ein Isolator hat ein nicht besetztes Leitungsband und eine so große Bandlücke (E_G> 3 eV), dass bei Raumtemperatur und auch bei deutlich höheren Temperaturen nur sehr wenige Elektronen vom Valenz- ins Leitungsband thermisch angeregt werden. Der spezifische Widerstand eines solchen Kristalls ist sehr hoch. Es gibt jedoch auch Isolatoren, auf die das Bändermodell nicht anwendbar ist.

Halbleiter

Ähnlich liegen die Verhältnisse bei einem Halbleiter, jedoch ist die Bandlücke hier so klein (1 eV < E_G < 3 eV), dass sie durch thermische Energiezufuhr überwunden werden kann. Ein Elektron kann ins Leitungsband angehoben werden und ist hier beweglich. Zugleich hinterlässt es im Valenzband eine Lücke, die durch benachbarte Elektronen aufgefüllt werden kann. Somit ist im Valenzband die Lücke beweglich. Man bezeichnet sie auch als Defektelektron, Elektronenfehlstelle oder Loch (siehe Löcherleitung). Bei Raumtemperatur weist ein Halbleiter dadurch eine geringe Eigenleitfähigkeit auf, die durch Temperaturerhöhung gesteigert werden kann.

Durch Dotierung kann ein Halbleiter gezielt mit Ladungsträgern ausgestattet werden. Der Halbleiterkristall beruht auf einem Kristallgitter aus 4-wertigen Atomen, die jeweils durch vier Elektronenpaare gebunden sind. Dotierung mit 5-wertigen Atomen hinterlässt im Gitter ein für die Bindung nicht erforderliches Elektron, das somit nur locker gebunden ist (Abbildung unten, Bild a). Mit nur geringer Energie kann es daher ins Leitungsband angehoben werden und ist hier beweglich (Bild b). Ein solches Atom nennt man einen Elektronen-Donator (lateinisch donare = geben). Der Kristall wird mit beweglichen negativen Ladungsträgern ausgestattet, man spricht von einer n-Dotierung. Zugleich bleibt ein positiver Atomrumpf im Gitter zurück. Lässt man den Hintergrund der neutralen Grundsubstanz außer Betracht (Bild c), so hat man eine positive feste und eine negative bewegliche Ladung ins Gitter eingebracht. Energetisch liegt ein Donator knapp unterhalb des Leitungsbandes, da wegen der schwachen Bindung des „zusätzlichen“ Elektrons wenig Energie zur Anregung ins Leitungsband vonnöten ist (Bild d).

Dotierung mit 3-wertigen Atomen führt zu einer ungesättigten Bindung, in der ein Elektron fehlt. Dieses kann mit geringem Energieaufwand aus einer anderen Bindung gerissen werden. Ein solches Atom nennt man einen Elektronen-Akzeptor (lat. accipere = annehmen), das energetisch knapp oberhalb des Valenzbandes liegt. Es entsteht eine negative ortsfeste Ladung. Zugleich hinterlässt das Elektron im Kristall eine Lücke, die durch ein anderes Elektron aufgefüllt werden kann, also eine bewegliche Elektronenfehlstelle. Im Resultat hat man eine negative feste und eine positive bewegliche Ladung eingebracht. Man spricht dann von p-Dotierung.

Dotierung von Halbleitern

Eine wichtige Anwendung finden die dotierten Kristalle in der Mikroelektronik, deren Strukturen vor allem auf Halbleiterdioden beruhen. Diese werden aus einem p-n-Übergang gebildet, das heißt aus einer Kombination eines p-dotierten mit einem n-dotierten Kristall.

Metalle und Halbmetalle

In einem Metall spricht man meist nicht von Leitungs- bzw. Valenzband. Bei einwertigen Metallen ist das höchste besetzte Energieband zur Hälfte aufgefüllt. Bei mehrwertigen Metallen überlappen sich teilweise Energiebänder. Elektronen können daher beim Anlegen von beliebig kleinen elektrischen Feldstärken in einen höheren Energiezustand wechseln (sich sozusagen frei bewegen) und zum elektrischen Strom beitragen, deswegen sind Metalle gute elektrische Leiter. Eine Temperaturerhöhung führt im Allgemeinen zur Verringerung der Leitfähigkeit des Kristalls, da die erhöhte Streuung der Elektronen eine niedrigere mittlere Geschwindigkeit bedingt. Das Ferminiveau liegt bei Metallen bzw. Halbmetallen innerhalb des höchsten besetzten Bandes bzw. im Überlappungsbereich der Bänder.

Bei Halbmetallen liegt die Unterkante des Leitungsbands etwas tiefer als die Oberkante des Valenzbandes. Diese Überlappung führt zu einer geringen Konzentration von Elektronen im Leitungsband und Löchern im Valenzband.

E-k-Diagramm

In den Abbildungen oben sind die Energieniveaus eindimensional über der Ortskoordinate x aufgetragen. Für die Betrachtung der Vorgänge beim Sprung eines Elektrons von einem Band zum anderen hat sich dagegen die Darstellung über dem Wellenvektor 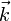$\vec k$ bewährt. Dies wird unter dem Stichwort Bandstruktur genauer erläutert.