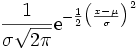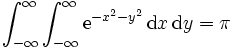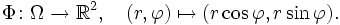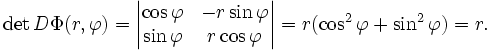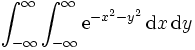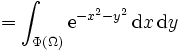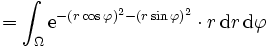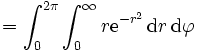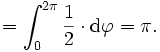- Trafosatz
-
Der Transformationssatz (auch Transformationsformel) beschreibt in der Analysis das Verhalten von Integralen unter Koordinatentransformationen. Es ist somit die Verallgemeinerung der Integration durch Substitution auf Funktionen höherer Dimensionen. Der Transformationssatz wird als Hilfsmittel bei der Berechnung von Integralen verwendet, wenn sich die zu integrierende Funktion nach Überführung in ein anderes Koordinatensystem leichter auflösen lässt.
Es sei
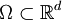 offen und
offen und 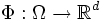 ein Diffeomorphismus. Dann ist f auf Φ(Ω) genau dann integrierbar, wenn
ein Diffeomorphismus. Dann ist f auf Φ(Ω) genau dann integrierbar, wenn 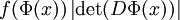 auf Ω integrierbar ist. In diesem Fall gilt:
auf Ω integrierbar ist. In diesem Fall gilt: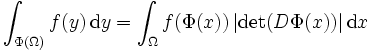 .
.
DΦ ist dabei die zugehörige Jacobi-Matrix.
Der Beweis läuft darauf hinaus, Eigenschaften einer solchen Transformation zu zeigen, die mit denen übereinstimmen, welche die Determinante eindeutig definieren.
Beispiel
Um zu zeigen, dass das Integral über die Gauß-Glocke
gleich 1 ist, genügt es, die Aussage
zu beweisen. Da die Funktion
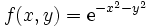 rotationssymmetrisch ist, liegt die Berechnung des Integrals in Polarkoordinaten statt kartesischen Koordinaten nahe:
rotationssymmetrisch ist, liegt die Berechnung des Integrals in Polarkoordinaten statt kartesischen Koordinaten nahe:Es sei
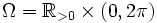 und
undDann ist die Funktionaldeterminante
Das Komplement von
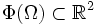 ist eine Nullmenge, mit
ist eine Nullmenge, mit 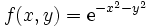 ergibt sich also
ergibt sich alsoDie Auswertung des inneren Integrals in der vorletzten Zeile kann beispielsweise durch eine Substitution t = r2 begründet werden.
Literatur
- Otto Forster: Analysis 3. Integralrechnung im Rn mit Anwendungen. 3. Aufl. Vieweg-Verlag, 1996. ISBN 3-528-27252-X
- Konrad Königsberger: Analysis 2, Springer, Berlin 2004.
Wikimedia Foundation.