Transkritische Bifurkation

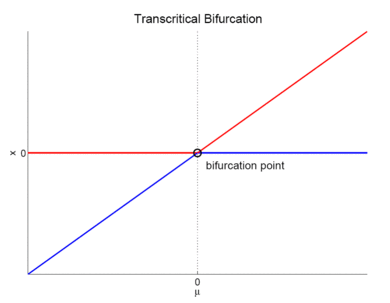Bifurkationsdiagramm einer Transkritischen Bifurkation. Stabile Fixpunkte sind rot, instabile blau dargestellt.

Die Transkritische Bifurkation ist ein bestimmter Typ einer Bifurkation eines nichtlinearen Systems.

Die Normalform der Transkritischen Bifurkation ist:

$\frac{dx}{dt} = \mu \cdot x - x^2$ (i)

wobei μ der Bifurkationsparameter ist.

Die Transkritische Bifurkation hat folgende Gleichgewichtspunkte:

${x_1}^* = 0$

${x_2}^* = \mu$

Die Anzahl an Gleichgewichtspunkten verhält sich also für eine Änderung des Parameter μ folgendermaßen:

$\mu < 0 : \mathrm{GGW} = \lbrace \mu, 0 \rbrace\,$

$\mu = 0 : \mathrm{GGW} = \lbrace 0 \rbrace\,$

$\mu > 0 : \mathrm{GGW} = \lbrace0, \mu\rbrace\,$

Die Anzahl an Gleichgewichtspunkten wechselt also von 2 zu 1 zu 2.

Diskretes System

Für ein diskretes System wird aus (i):

$x_{t+1} = x_t + \mu \cdot x_t - x_t^2$

Die Lage der Fixpunkte bleibt gegenüber dem kontinuierlichen System unverändert.

Siehe auch

Pitchfork-Bifurkation, Hopf-Bifurkation, Saddle-Node-Bifurkation, Bifurkation (Mathematik)