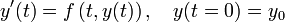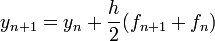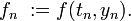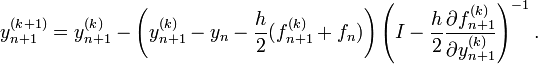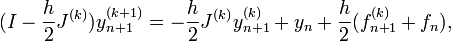Trapezmethode

Das implizite Trapez-Verfahren ist ein Verfahren zur numerischen Lösung eines Anfangswert-Problems

$y'(t) = f\left(t, y(t)\right), \quad y(t=0) = y_0$

Es lässt sich sowohl den Runge-Kutta-Verfahren als auch den Adams-Moulton-Verfahren zuordnen. Das Trapezverfahren ist A-stabil mit der Besonderheit, dass für die Schwingungslösung y'=iα_iy kein Amplitudenfehler auftritt^[1]. Das Verfahren lässt sich aus der Trapezregel herleiten:

$y_{n+1}=y_n + \frac{h}{2}(f_{n+1}+f_n)$

mit

$f_n \ := f(t_n,y_n).$

Lösungsmethode

Zur Lösung dieses, in der Regel nichtlinearen Gleichungssystems können verschiedene numerische Verfahren zur Lösung nichtlinearer Gleichungssysteme genutzt werden. Für das quadratisch konvergente Newton-Verfahren ergibt sich konkret:

$y^{(k + 1)}_{n+1} = y^{(k)}_{n+1} - \left( y^{(k)}_{n+1} - y_n - \frac{h}{2}(f^{(k)}_{n+1} + f_n) \right) \left(I - \frac{h}{2}\frac{\partial f^{(k)}_{n+1}}{\partial y^{(k)}_{n+1}}\right)^{-1}.$

Man erhält also ein lineares Gleichungssystem

$(I-\frac{h}{2} J^{(k)})y^{(k + 1)}_{n+1} = -\frac{h}{2} J^{(k)} y^{(k)}_{n+1} +y_n + \frac{h}{2}(f^{(k)}_{n+1} + f_n),$

wobei J die Jacobi-Matrix

$J^{(k)} := \left(\frac{\partial f}{\partial y}\right)^{(k)}_{n+1}$,

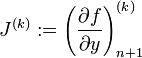I die Einheitsmatrix und k der Iterationsschritt ist.

Schrittweite h

Die (variable) Schrittweite kann aus folgender Beziehung berechnet werden:

$\vert\frac{F(h\lambda)}{e^{h\lambda}} - 1\vert = \delta$;

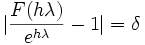δ bezeichnet den zugelassenen lokalen Diskretisierungsfehler. Der Ansatz 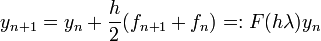$y_{n+1}=y_n+\frac{h}{2}(f_{n+1} + f_n)=:F(h\lambda)y_n$ liefert für die implizite Trapez-Methode

$F(h\lambda)=\frac{2+h\lambda}{2-h\lambda}$.

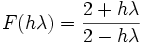Dabei ist 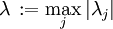$\lambda \, := \max_j{|\lambda_j|}$ der Betrag des betragsmäßig größten Eigenwerts der Jacobi-Matrix (Spektralradius). Die numerische Bestimmung der Eigenwerte ist sehr zeitaufwendig; für den Zweck der Schrittweitenberechnung ist es im Allgemeinen ausreichend die Gesamtnorm 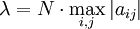$\lambda = N \cdot \max_{i,j} |a_{i j}|$ heranzuziehen, die immer größer oder gleich der Spektralnorm ist. N ist der Rang der Jacobi-Matrix und a_ij deren Elemente.

Literatur

• H. R. Schwarz: Numerische Mathematik, B.G.Teubner Stuttgart; 1986

Einzelnachweise

1. ↑ M. Kloker: Numerische Löser für die Gewöhnliche Modelldifferentialgleichung y'=αy, Universität Stuttgart, 1996