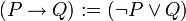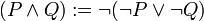- True Wert
-
Die Aussagenlogik (veraltet Urteilslogik) ist der Bereich der Logik, der sich mit Aussagen und deren Verknüpfung durch Junktoren befasst, ausgehend von strukturlosen Elementaraussagen (Atomen), denen semantisch ein Wahrheitswert zugeordnet wird.
Der Artikel befasst sich mit der klassischen Aussagenlogik.
Zur Geschichte
Historisch geht die Aussagenlogik zurück bis zu Aristoteles, der erstmals aussagenlogische Grundsätze diskutierte, nämlich in seiner Metaphysik den Satz vom Widerspruch und den Satz vom ausgeschlossenen Dritten, und der in seiner ersten Analytik den indirekten Beweis thematisierte. Die zweiwertige aussagenlogische Semantik entwickelten etwas später die megarischen Philosophen Diodoros Kronos und Philon. Die Aussagensemantik und -axiomatik kombinierte der Stoiker Chrysippos von Soli, der den ersten aussagenlogischen Kalkül formulierte. Die Weiterentwicklung der Aussagenlogik der Stoa durch das Mittelalter wird oft übersehen.[1] Eine erste vollständige und entscheidbare Formalisierung für aussagenlogische Tautologien – allerdings noch nicht für das aussagenlogische Schließen – schuf George Boole 1847 mit seinem algebraischen Logikkalkül. Den ersten aussagenlogischen Kalkül mit Schlussregeln formulierte Gottlob Frege im Rahmen seiner Begriffsschrift 1879. Er war die Vorlage für den Aussagenkalkül von Bertrand Russell 1910, der sich später durchsetzte (s. u.).
Zur Abgrenzung der klassischen Aussagenlogik
Da in der heutigen Mathematik die klassische Aussagenlogik maßgeblich wurde, wird in diesem Artikel nur dieser moderne Haupttypus der Aussagenlogik behandelt. Allgemein ist die klassische Logik durch zwei Eigenschaften charakterisiert:
- Jede Aussage hat einen von genau zwei Wahrheitswerten, meist „falsch“ oder „wahr“ (Prinzip der Zweiwertigkeit oder Bivalenzprinzip).
- Der Wahrheitswert jeder zusammengesetzten Aussage ist eindeutig durch die Wahrheitswerte ihrer Teilaussagen bestimmt (Prinzip der Extensionalität oder Kompositionalität, siehe Extensionalitätsprinzip)
Das Prinzip der Zweiwertigkeit wird oft mit dem Satz vom ausgeschlossenen Dritten verwechselt.
Die klassische Aussagenlogik ist jenes Teilgebiet der klassischen Logik, das die innere Struktur von Sätzen (Aussagen) nur daraufhin untersucht, aus welchen anderen Sätzen (Teilsätzen) sie zusammengesetzt sind. Die innere Struktur von Sätzen, die ihrerseits nicht in weitere Teilsätze zerlegt werden können, wird von der Aussagenlogik nicht betrachtet. Ein Beispiel: Die Aussage „Alle Katzen sind Hunde, und die Erde ist eine Scheibe“ ist mit dem Bindewort „und“ aus den beiden kürzeren Aussagen „Alle Katzen sind Hunde“ und „Die Erde ist eine Scheibe“ zusammengesetzt. Diese beiden Aussagen lassen sich ihrerseits nicht mehr in weitere Aussagen zerlegen, sind aus aussagenlogischer Sicht also elementar oder atomar. Andere, auf die Aussagenlogik aufbauende logische Systeme betrachten die innere Struktur solcher atomaren Aussagen; ein wichtiges Beispiel ist die Prädikatenlogik.
In Abgrenzung zur klassischen Logik entstehen nichtklassische Logiksysteme, wenn man das Prinzip der Zweiwertigkeit, das Prinzip der Extensionalität oder sogar beide Prinzipien aufhebt. Nichtklassische Logiken, die durch die Aufhebung des Prinzips der Zweiwertigkeit entstehen, heißen mehrwertige Logik. Die Zahl der Wahrheitswerte (vielleicht besser: Pseudowahrheitswerte) kann dabei endlich sein (z. B. dreiwertige Logik), ist aber oft auch unendlich (z. B. Fuzzy-Logik). Hingegen verwenden Logiken, die durch die Aufhebung der Extensionalität entstehen, Junktoren (Konnektive), bei denen sich der Wahrheitswert des zusammengesetzten Satzes nicht mehr eindeutig aus dem Wahrheitswert seiner Teile bestimmen lässt. Ein Beispiel für nichtextensionale Logik ist die Modallogik, die die einstelligen nichtextensionalen Operatoren „es ist notwendig, dass“ und „es ist möglich, dass“ einführt.
Logische Systeme stehen innerhalb der Logik nicht in einem Konkurrenzverhältnis um Wahrheit oder Richtigkeit. Die Frage, welches logische System für einen bestimmten Zweck genützt werden soll, ist eher eine pragmatische.
Oft werden logische Systeme und logische Fragestellungen mit außerlogischen Fragen verwechselt oder vermischt, z. B. mit der metaphysischen Frage, welches logische System „richtig“ sei, d. h. die Wirklichkeit beschreibe. Zu dieser Frage gibt es unterschiedliche Standpunkte einschließlich des positivistischen Standpunkts, dass diese Frage sinnlos sei. Diese Fragen fallen aber in andere Gebiete, z. B. Philosophie, Wissenschaftstheorie und Sprachwissenschaft.
Wenn in diesem Artikel die klassische Aussagenlogik behandelt wird, so ist das also nicht als metaphysische Festlegung zu verstehen oder gar als Behauptung, dass „alle Aussagen wahr oder falsch sind“. Es ist lediglich so, dass die klassische Aussagenlogik einfach nur solche Aussagen behandelt, die wahr oder falsch sind. Das ist eine große formale Vereinfachung, die dieses System relativ leicht erlernbar sein lässt. Braucht man aus metaphysischen oder pragmatischen Gründen mehr als zwei Wahrheitswerte, ist es auf dem Fundament der klassischen Aussagenlogik ein Leichtes, ein geeignetes logisches System aufzustellen.
Umgangssprachliche Einleitung
Einfache Aussage (Elementaraussage)
Eine Aussage A ist ein Satz, der entweder wahr (w, wahr, true, 1) oder nicht wahr (f, falsch, false, 0) ist. Dies gilt sowohl für einfache als auch für verknüpfte Aussagen. „Halbwahrheiten“ gibt es nicht. Eine Aussage kann sowohl der gewöhnlichen Sprache entstammen als auch der Sprache der Mathematik.
Beispiele für einfache Aussagen:
- A1: München ist 781 km von Hamburg entfernt.
- A2: 9 ist durch 3 teilbar.
- A3: Eintracht Frankfurt wird in der nächsten Saison deutscher Fußballmeister.
- A4: Alle Autos sind grün.
A2 ist offensichtlich wahr, A4 dagegen ist falsch. A1 muss man zunächst prüfen, bevor man entscheiden kann, ob A1 wahr oder falsch ist. Ob A3 wahr ist, kann man derzeit nicht entscheiden. Das wird sich erst am Ende der nächsten Fußballsaison herausstellen.
In der klassischen Aussagenlogik ist eine Aussage entweder wahr oder nicht wahr, auch wenn man (noch) nicht in der Lage ist, den Wahrheitsgehalt zu beurteilen. Dies ist zum Beispiel bei den ungelösten mathematischen Problemen der Fall.
Anmerkung: A4 ist eine All-Aussage; die Struktur solcher Aussagen ist Gegenstand der Prädikatenlogik. Im Sinne der Aussagenlogik ist es eine Elementaraussage.
Verneinte Aussage – Negation
Die Verneinung bzw. Negation (auch: Satzverneinung, äußere Verneinung, kontradiktorisches Gegenteil) einer Aussage A ist diejenige Aussage ¬A, die genau dann wahr ist, wenn A falsch ist, und die genau dann falsch ist, wenn A wahr ist. Einfacher: Die Verneinung einer Aussage A dreht den Wahrheitswert von A in sein Gegenteil um.
Man erhält die Verneinung einer Aussage A immer dadurch, dass man ihr die Formulierung „Es ist nicht der Fall, dass“ voranstellt. Zwar lässt sich ein natürlichsprachlicher Satz auch verneinen, indem man das Wort „nicht“ oder eine andere negative Formulierung an geeigneter Stelle einfügt – es ist aber nicht immer ganz einfach, zu erkennen, welche Formulierung und an welcher Stelle. Formal schreibt man für „nicht A“ in der gebräuchlichsten Notation (Schreibweise) ¬A, auf Englisch und in der Schaltalgebra auch „NOT A“, gelegentlich auch „~A“.
A 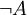
falsch wahr wahr falsch Wir verneinen die obigen Beispiele:
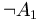 : Es ist nicht der Fall, dass München 781 km von Hamburg entfernt ist.
: Es ist nicht der Fall, dass München 781 km von Hamburg entfernt ist.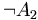 : Es ist nicht der Fall, dass 9 durch 3 teilbar ist.
: Es ist nicht der Fall, dass 9 durch 3 teilbar ist.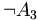 : Es ist nicht der Fall, dass Eintracht Frankfurt in der nächsten Saison deutscher Fußballmeister wird.
: Es ist nicht der Fall, dass Eintracht Frankfurt in der nächsten Saison deutscher Fußballmeister wird.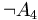 : Es ist nicht der Fall, dass alle Autos grün sind. Es kann aber durchaus auch grüne Autos geben und es gibt auch Autos, die nicht grün sind.
: Es ist nicht der Fall, dass alle Autos grün sind. Es kann aber durchaus auch grüne Autos geben und es gibt auch Autos, die nicht grün sind.
Allgemein gilt für die Verneinung:
- Wenn eine Aussage A wahr ist, ist die Verneinung
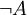 falsch.
falsch. - Wenn eine Aussage A falsch ist, ist die Verneinung
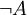 wahr.
wahr. - Eine Aussage A kann nicht gleichzeitig wahr und falsch sein.
- Die Aussagen A und
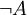 können nicht gleichzeitig wahr sein.
können nicht gleichzeitig wahr sein.
Und-verknüpfte Aussagen – Konjunktion
Eine Konjunktion ist eine aus zwei Aussagen zusammengesetzte Aussage, die die Wahrheit all ihrer Teilaussagen behauptet. Umgangssprachlich verbindet man zwei Aussagen A und B durch das Bindewort „und“ zu einer Konjunktion „A und B“, in der logischen Sprache verwendet man meist das Zeichen
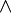 (Schreibweise:
(Schreibweise: 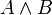 ), gelegentlich auch das kaufmännische Und, den Ampersand (&).
), gelegentlich auch das kaufmännische Und, den Ampersand (&).- Sprechweise: A und B
- Schreibweise:
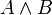
- auf Englisch und in der Schaltalgebra auch A AND B
Die Aussage
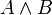 ist immer dann wahr, wenn sowohl A als auch B jeweils wahr sind. Andernfalls ist
ist immer dann wahr, wenn sowohl A als auch B jeweils wahr sind. Andernfalls ist 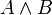 falsch, nämlich dann, wenn entweder A oder B oder beide Aussagen falsch sind.
falsch, nämlich dann, wenn entweder A oder B oder beide Aussagen falsch sind.Beispiele für eine und-Verknüpfung:
A: 9 ist durch 3 teilbar
B: 9 ist eine QuadratzahlA B 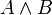
wahr wahr wahr falsch wahr falsch wahr falsch falsch falsch falsch falsch Diese Teilaussagen und ihre Negationen werden nun durch
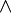 miteinander verknüpft:
miteinander verknüpft:- C1: 9 ist durch 3 teilbar und 9 ist eine Quadratzahl.
- C2: 9 ist nicht durch 3 teilbar und 9 ist eine Quadratzahl.
- C3: 9 ist durch 3 teilbar und 9 ist keine Quadratzahl.
- C4: 9 ist nicht durch 3 teilbar und 9 ist keine Quadratzahl.
Nur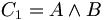 ist wahr, weil A wahr ist und auch B wahr ist.
ist wahr, weil A wahr ist und auch B wahr ist.
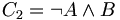 ist falsch, weil
ist falsch, weil 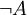 falsch ist.
falsch ist.
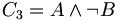 ist falsch, weil
ist falsch, weil 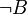 falsch ist.
falsch ist.
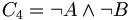 ist falsch, weil sowohl
ist falsch, weil sowohl 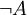 als auch
als auch 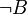 falsch ist.
falsch ist.Nichtausschließendes Oder – Disjunktion
Eine Disjunktion ist eine zusammengesetzte Aussage, die behauptet, dass mindestens eine ihrer Teilaussagen wahr ist. Die Disjunktion in diesem Sinn wird auch nichtausschließendes Oder genannt. (Aber Achtung: Die Bezeichnung „Disjunktion“ wurde und wird oft auch für das ausschließende Oder, „entweder … oder“, verwendet. Einige Autoren verwenden daher für das Nichtausschließende Oder den Begriff Adjunktion.)
- Sprechweise: „A oder B“; genauer: „A oder B (oder beide)“, häufig in juristischen oder medizinischen Texten: „A und/oder B“
- Schreibweise:
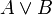
- auf Englisch und in der Schaltalgebra auch A OR B
Die Aussage
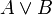 ist immer dann wahr, wenn mindestens eine der Teilaussagen A oder B wahr ist, bzw. wenn beide Teilaussagen wahr sind. Andernfalls ist
ist immer dann wahr, wenn mindestens eine der Teilaussagen A oder B wahr ist, bzw. wenn beide Teilaussagen wahr sind. Andernfalls ist 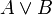 falsch, nämlich dann, wenn sowohl A als auch B falsch sind.
falsch, nämlich dann, wenn sowohl A als auch B falsch sind.Beispiel für eine oder-Verknüpfung:
- A: 9 ist durch 3 teilbar
- B: 9 ist eine Quadratzahl
A B 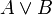
wahr wahr wahr falsch wahr wahr wahr falsch wahr falsch falsch falsch Diese Teilaussagen und ihre Negationen werden nun durch
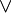 miteinander verknüpft:
miteinander verknüpft:- C5: 9 ist durch 3 teilbar oder 9 ist eine Quadratzahl.
- C6: 9 ist nicht durch 3 teilbar oder 9 ist eine Quadratzahl.
- C7: 9 ist durch 3 teilbar oder 9 ist keine Quadratzahl.
- C8: 9 ist nicht durch 3 teilbar oder 9 ist keine Quadratzahl.
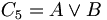 ist wahr, weil sowohl A als auch B wahr sind.
ist wahr, weil sowohl A als auch B wahr sind.
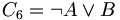 ist wahr, weil B wahr ist.
ist wahr, weil B wahr ist.
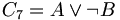 ist wahr, weil A wahr ist.
ist wahr, weil A wahr ist.
Nur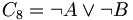 ist falsch, weil
ist falsch, weil 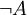 falsch ist und auch
falsch ist und auch 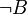 falsch ist.
falsch ist.Materiale Implikation
Die materiale Implikation, auch Konditional oder Subjunktion genannt (siehe Implikation), drückt die hinreichende Bedingung aus: Sie sagt, dass die Wahrheit des einen Satzes eine hinreichende Bedingung für die Wahrheit des anderen Satzes ist. Man schreibt
oder auch
und liest
- A ist eine hinreichende Bedingung für B.
- Schon wenn A, dann B.
- A setzt voraus, dass B.
- B ist eine notwendige Bedingung für A.
Dass B genau dann eine notwendige Bedingung für A ist, wenn A eine hinreichende Bedingung für B ist, ist eine auf den ersten Blick überraschende und vielleicht kontraintuitive, jedoch zutreffende Feststellung. Das Unterkapitel Hinreichende und notwendige Bedingung bemüht sich, diesen Zusammenhang sichtbarer zu machen. - Nur wenn B, dann A.
oder auch nur
- Wenn A, dann B.
In einem Konditional nennt man A das Antezedens, B das Konsequens oder Sukzedens.
Beispiele:
- Dass es regnet, ist eine hinreichende Bedingung dafür, dass die Straße nass ist.
- Schon wenn es regnet, ist die Straße nass.
- Wenn es regnet, ist die Straße nass.
- Nur wenn die Straße nass ist, regnet es.
- Wenn Person x einen Wagen der Marke BMW hat, hat x ein Auto.
- Wenn eine Zahl n durch 6 teilbar ist, dann ist die Zahl n durch 3 teilbar.
Die Lesart „wenn … dann“ ist insofern problematisch, als mit dem natürlichsprachlichen „wenn … dann“ vor allem inhaltliche Zusammenhänge wie Kausalität oder zeitliche Nähe ausgedrückt werden. All das macht die materiale Implikation nicht, sie nennt nur den formalen Zusammenhang: „Dass es regnet, ist eine hinreichende Bedingung dafür, dass die Straße nass ist“. Zur Frage, warum das eine hinreichende Bedingung ist – ob auf Grund eines kausalen Zusammenhangs oder auch nur rein zufällig –, nimmt die materiale Implikation nicht Stellung (mehr hierzu im Artikel Implikation).
A B 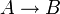
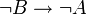
falsch falsch wahr wahr falsch wahr wahr wahr wahr falsch falsch falsch wahr wahr wahr wahr Als Umkehrschluss bezeichnet man den Schluss von
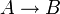 auf
auf 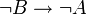 . Für die Beispiele bedeutet das:
. Für die Beispiele bedeutet das:- Wenn die Straße nicht nass ist, regnet es nicht.
- Nur wenn es nicht regnet ist die Straße nicht nass.
- Wenn Person x kein Auto hat, dann hat x keinen Wagen der Marke BMW.
- Nur wenn Person x keinen Wagen der Marke BMW hat, hat x kein Auto.
- Wenn die Zahl n nicht durch 3 teilbar ist, dann ist n nicht durch 6 teilbar.
- Nur wenn n nicht durch 6 teilbar ist, ist n nicht durch 3 teilbar.
Umgangssprachlich lässt man sich gelegentlich zu weiteren – falschen – Aussagen verleiten:
- Weil es nicht regnete, kann die Straße nicht nass sein.
Diese Folgerung ist falsch, da die Straße auch aus anderen Gründen nass werden kann (Rohrbruch, Übung der Feuerwehr ...). - x hat keinen Wagen der Marke BMW, also hat x kein Auto.
falsch, denn er könnte ja einen Mercedes haben - n ist nicht durch 6 teilbar, also ist n auch nicht durch 3 teilbar.
Auch diese Folgerung ist falsch. Die Zahl 15 ist nicht durch 6 teilbar und sehr wohl durch 3.
Das bedeutet: Wenn die Folgerung
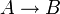 wahr ist, dann erhält man aus der Aussage ¬A keine Aussage über B; B kann wahr oder falsch sein. („Ex falso sequitur quodlibet“ – „Aus Falschem folgt Beliebiges“)
wahr ist, dann erhält man aus der Aussage ¬A keine Aussage über B; B kann wahr oder falsch sein. („Ex falso sequitur quodlibet“ – „Aus Falschem folgt Beliebiges“)Die Implikation ist ein wichtiges Mittel in der Mathematik. Die meisten mathematischen Sätze sind als Implikationen formuliert.
Bikonditional
Das Bikonditional, oft auch objektsprachliche Äquivalenz oder materiale Äquivalenz genannt, drückt die hinreichende und notwendige Bedingung aus, sagt also, dass eine Aussage A genau dann zutrifft, wenn eine Aussage B zutrifft. Man schreibt:
und liest
- A ist genau dann der Fall, wenn B der Fall ist.
- A genau dann wenn B.
- A ist dann und nur dann der Fall, wenn B der Fall ist.
Auch beim Bikonditional wird eine rein formale Aussage getroffen, die nichts über einen allfälligen inhaltlichen Zusammenhang von A und B aussagt.
Statt
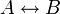 zu sagen, kann man auch sagen, dass A eine hinreichende Bedingung für B und dass B eine hinreichende Bedingung für A ist, also
zu sagen, kann man auch sagen, dass A eine hinreichende Bedingung für B und dass B eine hinreichende Bedingung für A ist, also 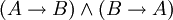 . Tatsächlich sind diese beiden Aussagen logisch äquivalent.
. Tatsächlich sind diese beiden Aussagen logisch äquivalent.A B 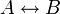
falsch falsch wahr falsch wahr falsch wahr falsch falsch wahr wahr wahr Beispiel:
- Die ganze Zahl n ist genau dann durch 6 teilbar, wenn n durch 2 und durch 3 teilbar ist.
Wenn n durch 6 teilbar ist, dann folgt daraus, dass n durch 2 und durch 3 teilbar ist. Umgekehrt gilt aber auch: Wenn n durch 2 und durch 3 teilbar ist, dann ist n durch 6 teilbar. - Heute ist genau dann Dienstag, wenn morgen Mittwoch ist.
- Die Erde ist genau dann eine Scheibe, wenn man bei einer ausgedehnten Segelpartie in den Weltraum stürzen kann.
Das Bikonditional als zusammengesetzte Aussage innerhalb der logischen Sprache (siehe Objektsprache) wird oft mit dem Konzept der logischen Äquivalenz verwechselt oder vermischt. Die logische Äquivalenz ist eine metasprachliche, meist natürlichsprachlich formulierte Eigenschaft zweier Aussagen der logischen Sprache. Ein Zusammenhang zwischen logischer Äquivalenz und Bikonditional besteht nur insofern, als das Metatheorem gilt, dass ein Bikonditional
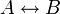 genau dann eine Tautologie ist, wenn die beiden Aussagen A und B logisch äquivalent sind.
genau dann eine Tautologie ist, wenn die beiden Aussagen A und B logisch äquivalent sind.Ausschließendes Oder
A B 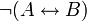
falsch falsch falsch falsch wahr wahr wahr falsch wahr wahr wahr falsch Das ausschließende Oder (Kontravalenz oder Antivalenz), „entweder A oder B“, besagt, dass genau eine der beiden von ihm verknüpften Aussagen wahr ist. Entsprechend ist ein ausschließendes Oder nicht nur dann falsch, wenn sowohl A als auch B falsch sind, sondern auch, wenn beide wahr sind. (Einige Autoren verwenden für das Ausschließende Oder den Begriff Alternative.)
Obwohl das ausschließende Oder ein Konzept ist, mit dem man in der natürlichen Sprache immer wieder zu tun hat, wird es in den meisten logischen Sprachen nicht als eigenständiger Junktor eingeführt. Statt dessen wird das ausschließende Oder zum Beispiel als verneintes Bikonditional ausgedrückt, also als
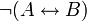 .
.Große Bedeutung genießt das ausschließende Oder hingegen in der Schaltalgebra, wo es meist als XOR (eXclusive OR) aufgeschrieben wird.
Verneinung einer verknüpften Aussage (De Morgansche Gesetze)
- Hauptartikel: De Morgansche Gesetze
Verneinung einer Konjunktion
Die Verneinung der Konjunktion „A und B“ (in der logischen Schreibweise:
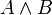 ) lautet „Es ist nicht der Fall, dass A und B zutreffen“ (in der logischen Schreibweise:
) lautet „Es ist nicht der Fall, dass A und B zutreffen“ (in der logischen Schreibweise: 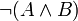 ). Diese ist logisch äquivalent mit der Aussage „A ist nicht der Fall, oder B ist nicht der Fall (oder beides)“ (in logischer Schreibweise:
). Diese ist logisch äquivalent mit der Aussage „A ist nicht der Fall, oder B ist nicht der Fall (oder beides)“ (in logischer Schreibweise: 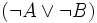 ).
).A B 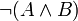
falsch falsch wahr falsch wahr wahr wahr falsch wahr wahr wahr falsch Ein Beispiel:
Wenn man die Aussage
- Es regnet, und die Erde ist eine Scheibe
verneinen möchte, dann kann man entweder sagen
- Es ist nicht der Fall, dass es regnet und die Erde eine Scheibe ist.
oder man sagt
- Es regnet nicht oder die Erde ist keine Scheibe (oder beides).
In der Schaltalgebra wird sehr oft der Junktor NAND verwendet, wobei „A NAND B“ denselben Wahrheitswertverlauf hat wie der Ausdruck „
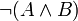 “.
“.Verneinung einer Disjunktion
Die Verneinung der Disjunktion „A oder B (oder beides)“ (in der logischen Schreibweise:
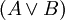 ) lautet „Es ist nicht der Fall, dass A oder B zutrifft“ (in logischer Schreibweise:
) lautet „Es ist nicht der Fall, dass A oder B zutrifft“ (in logischer Schreibweise: 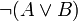 ). Diese ist logisch äquivalent mit der Aussage „A ist nicht der Fall, und B ist nicht der Fall“ (in logischer Schreibweise:
). Diese ist logisch äquivalent mit der Aussage „A ist nicht der Fall, und B ist nicht der Fall“ (in logischer Schreibweise: 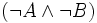 ).
).A B 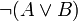
falsch falsch wahr falsch wahr falsch wahr falsch falsch wahr wahr falsch Ein Beispiel:
Wenn man die Aussage
- Die Erde ist eine Scheibe, oder die Erde ist ein Würfel.
verneinen möchte, so sagt man
- Es ist nicht der Fall, dass die Erde eine Scheibe ist oder dass die Erde ein Würfel ist.
Nach dem Gesetz von De Morgan kann man nun aber auch sagen:
- Die Erde ist keine Scheibe, und die Erde ist kein Würfel
oder in schönerem Deutsch
- Die Erde ist weder eine Scheibe noch ein Würfel.
In der Schaltalgebra wird das Konnektiv NOR verwendet, das denselben Wahrheitswertverlauf hat wie die Aussage
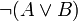 .
.Hinreichende und notwendige Bedingung
Dieser Abschnitt soll den zunächst oft als kontraintuitiv empfundenen Zusammenhang zwischen hinreichender und notwendiger Bedingung, wie er im Abschnitt über die materiale Implikation angesprochen wurde, wiederaufgreifen und näher ausführen.
Betrachten wir einmal mehr die materiale Implikation
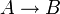 .
.Man sagt: A ist hinreichend für B: Schon wenn A der Fall ist, ist auch B der Fall.
Umgekehrt kann man aber auch sagen: B ist notwendig für A. Ohne B kann A nicht erfüllt sein.
Wie kommt dieser Zusammenhang zustande?
Wir wissen, dass die Wahrheit von A die Wahrheit von B nach sich zieht, denn A ist ja hinreichende Bedingung für B. Somit ist es einfach nicht möglich, dass A eintritt, ohne dass B damit ebenfalls eintreten würde: B ist also gezwungenermaßen der Fall, wenn A der Fall ist. B ist „notwendig“ für A.
Dieser Zusammenhang ist in Wahrheit also ziemlich einfach; Hauptgrund dafür, dass er anfangs oft als kontraintuitiv empfunden wird, ist wahrscheinlich die Schwierigkeit, zwischen den vielen Bedeutungen des umgangssprachlichen „wenn … dann“ einerseits und der rein formalen hinreichenden und notwendigen Bedingung andererseits strikt zu trennen.
Mit dem umgangssprachlichen „wenn … dann“ möchte man fast immer einen inhaltlichen (kausalen und/oder temporalen) Zusammenhang zwischen Antecedens und Konsequens ausdrücken: „Regen verursacht Straßennässe“, „Zuerst fällt der Regen, erst nachher wird die Straße nass“. Wenn man die hinreichende Bedingung in diesem Sinn missversteht, dann ist es klar, dass die in umgekehrter Reihenfolge formulierte notwendige Bedingung „Nur wenn die Straße nass ist, regnet es“ seltsam aussieht: „Regen verursacht doch Straßennässe, wie kann daraus je gefolgert werden, dass Straßennässe Regen verursacht?“
All dies sagt die materiale Implikation aber nicht aus. „A ist eine hinreichende Bedingung für B“ meint schlicht, dass wenn der Satz A wahr ist, auch der Satz B wahr ist – zeitlos und zusammenhanglos, nicht etwa „später“ oder „weil“.
Analog sagt die notwendige Bedingung, „B ist eine notwendige Bedingung für A“, lediglich das aus, dass B wahr ist, sofern A es ist. Genau das ist aber die Definition des Konditionals A → B.
Siehe auch: notwendige und hinreichende Bedingung
Formaler Zugang
Einleitung
Spätestens beim lauten Lesen von Sätzen wie:
- „Die Aussage
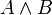 ist genau dann wahr, wenn die Aussagen A und B wahr sind“,
ist genau dann wahr, wenn die Aussagen A und B wahr sind“,
wird der selbstbewusste Laie verlangen, dass ihm erklärt wird, was das soll.
Die Antwort des Logikers: Es soll versucht werden, Sicherheit in die Regeln des logischen Schließens zu bringen. Seit den Sophisten ist dem Abendland klar, dass scheinbar zwingende Schlüsse zu offensichtlich absurden Ergebnisse führen können. Immer wieder wurden Paradoxien formuliert und von großen Denkern als Herausforderung empfunden. Logiker versuchen deshalb, die Regeln des Argumentierens so streng wie möglich zu fassen.
Das einleitende Beispiel macht klar, dass hierzu eine Trennung der Sprachebenen unerlässlich ist: Die formale Aussage A∧B soll dadurch erklärt werden, dass auf einer metasprachlichen Ebene über die Aussage A wie auch über die Aussage B geredet wird.
Ein Versuch dies durchzuführen, besteht darin, die Aussagenlogik als formales System, konkret als Kalkül (eine bestimmte Art formales System) zu definieren. Die Begriffe „wahr“ und „falsch“ kommen in diesem System zunächst überhaupt nicht vor. Statt dessen werden Axiome gesetzt, die einfach als Zeichenketten angesehen werden, aus denen weitere ableitbare Zeichenketten aufgrund von bestimmten Schlussregeln hergeleitet werden.
Natürlich ist das Ziel dabei, dass in einem formalen System nur Zeichenketten (Sätze) hergeleitet werden können, die bei einer plausiblen Interpretation auch wahr sind. Andererseits sollen alle Sätze, die als „wahr“ interpretierbar sind, auch hergeleitet werden können. Das erste ist die Forderung nach Korrektheit, das zweite die nach Vollständigkeit des formalen Systems; beide Eigenschaften sind unter Kalkül: Der Begriff Kalkül in der Logik beschrieben.
Für die klassische Aussagenlogik, mit der wir es hier zu tun haben, gibt es Kalküle (formale Systeme), die sowohl korrekt als auch vollständig sind. Für komplexere logische Systeme (z. B. Mengenlehre) ist es aber unmöglich, einen vollständigen Kalkül aufzustellen, der auch korrekt ist – diese Erkenntnis wurde 1931 von Kurt Gödel bewiesen (Gödelscher Unvollständigkeitssatz).
Syntax
Es gibt viele verschiedene Möglichkeiten, die Syntax („Grammatik“) einer logischen Sprache formal zu definieren; meist geschieht das im Rahmen eines Kalküls. Die folgende Definition ist daher nur als Beispiel dafür zu verstehen, wie ein Kalkül für die klassische Aussagenlogik aussehen kann. Weitere Beispiele für konkrete Kalküle finden sich unter Baumkalkül, Begriffsschrift, Systeme natürlichen Schließens, Sequenzenkalkül oder Resolutionskalkül. Ein weiterer axiomatischer Kalkül ist als Beispiel im Artikel Hilbert-Kalkül angegeben, ein graphischer Kalkül im Artikel Existential Graphs.
Bausteine der aussagenlogischen Sprache
Als Bausteine der aussagenlogischen Sprache sollen Satzbuchstaben („atomare Formeln“, Satzkonstanten), Junktoren und Gliederungszeichen verwendet werden. Satzbuchstaben sollen die Zeichen P0, P1, P2,... sein. Junktoren sollen die Zeichen ¬, ∧, ∨, → und ↔ sein. Als Gliederungszeichen sollen die runden Klammern dienen.
Formal lässt sich das z. B. auf folgende Weise ausdrücken:
Sei V die (abzählbar unendliche) Menge der atomaren Formeln (Satzbuchstaben):
- V = { Pn | n ∈ N0 } (N...Menge der natürlichen Zahlen inkl. 0), d. h. V = { P0, P1, P2, P3,... }
Sei J die Menge der Junktoren und Gliederungszeichen:
- J = { ¬, ∧, ∨, →, ↔, (, ) }
Das Alphabet der logischen Sprache sei die Menge V ∪ J, also die Vereinigungsmenge von atomaren Formeln, Junktoren und Gliederungszeichen.
Formationsregeln
Die Formationsregeln legen fest, wie man aus den Bausteinen der aussagenlogischen Sprache Sätze (Formeln) bilden kann.
Hier sollen aussagenlogische Formeln als Worte über dem Alphabet der logischen Sprache, also über V ∪ J wie folgt induktiv definiert werden:
- Alle atomaren Formeln F ∈ V (d. h. alle Satzbuchstaben) sind Formeln.
- Ist F eine Formel, so ist auch (¬F) eine Formel. (Diese Formel heißt Negation von F.)
- Sind F und G zwei (nicht notwendigerweise unterschiedliche) Formeln, so ist auch (F ∧ G) eine Formel. (Diese Formel heißt Konjunktion von F und G.)
- Sind F und G zwei (nicht notwendigerweise unterschiedliche) Formeln, so ist auch (F ∨ G) eine Formel. (Diese Formel heißt Disjunktion von F und G.)
- Sind F und G zwei (nicht notwendigerweise unterschiedliche) Formeln, so ist auch (F → G) eine Formel. (Diese Formel heißt materiale Implikation oder Konditional von F und G.)
- Sind F und G zwei (nicht notwendigerweise unterschiedliche) Formeln, so ist auch (F ↔ G) eine Formel. (Diese Formel heißt Bikonditional von F und G.)
- Nichts anderes ist eine aussagenlogische Formel.
Schlussregeln
Schlussregeln sind allgemein Transformationsregeln (Umformungsregeln), die auf bestehende Formeln angewandt werden und aus ihnen neue Formeln erzeugen. Wenn man einen Kalkül für ein logisches System aufstellt, dann wählt man die Transformationsregeln so, dass sie aus bestehenden Formeln solche Formeln erzeugen, die aus den Ausgangsformeln semantisch folgen – deshalb die Bezeichnung „Schlussregel“.
Innerhalb der Syntax sind die Schlussregeln allerdings rein formale Transformationsregeln, denen für sich keinerlei inhaltliche Bedeutung zukommt.
An konkreten Schlussregeln sollen hier nur zwei angegeben werden: Der Modus ponendo ponens und die Substitutionsregel.
- Modus ponendo ponens
- Aus einem Satz der Form
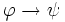 und einem Satz der Form
und einem Satz der Form  darf man auf einen Satz der Form ψ schließen; dabei sind
darf man auf einen Satz der Form ψ schließen; dabei sind  und ψ Platzhalter für beliebige Formeln. Zum Beispiel darf man nach dieser Schlussregel aus „Wenn Regen die Straße benetzt, dann ist der Straßenbelag regennass“ und aus „Regen benetzt die Straße“ schließen auf „Der Straßenbelag ist regennass“.
und ψ Platzhalter für beliebige Formeln. Zum Beispiel darf man nach dieser Schlussregel aus „Wenn Regen die Straße benetzt, dann ist der Straßenbelag regennass“ und aus „Regen benetzt die Straße“ schließen auf „Der Straßenbelag ist regennass“.
- Substitutionsregel (Ersetzungsregel)
- In einem Satz dürfen alle Vorkommnisse eines beliebigen Atoms (z. B. „P“) durch einen beliebig komplexen Satz (z. B.
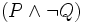 ) ersetzt werden. Es müssen dabei aber auch wirklich alle Vorkommnisse des gewählten Atoms ersetzt werden, und sie müssen auch wirklich alle durch denselben Satz ersetzt werden.
) ersetzt werden. Es müssen dabei aber auch wirklich alle Vorkommnisse des gewählten Atoms ersetzt werden, und sie müssen auch wirklich alle durch denselben Satz ersetzt werden. - Zum Beispiel darf mittels der Substitutionsregel aus
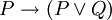 auf
auf 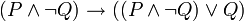 geschlossen werden. Man sagt, P werde durch
geschlossen werden. Man sagt, P werde durch 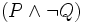 ersetzt bzw.
ersetzt bzw. 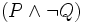 werde für P substituiert (eingesetzt).
werde für P substituiert (eingesetzt).
Für andere Beispiele von Schlussregeln siehe Schlussregel.
Siehe auch: Kalkül
Axiome
Axiome sind ausgezeichnete (im Sinn von: hervorgehobene) Formeln der aussagenlogischen Sprache. Die Auszeichnung besteht darin, dass sie innerhalb eines Beweises oder einer Herleitung (siehe unten) ohne weitere Rechtfertigung verwendet werden.
Pragmatisch wählt man solche Formeln als Axiome, die semantisch gesehen Tautologien sind, also immer zutreffen, und die dabei helfen, Beweise zu verkürzen. Innerhalb der Syntax sind die Axiome allerdings rein formale Objekte, denen keinerlei inhaltliche Bedeutung oder Rechtfertigung zukommt.
Axiome sind im Allgemeinen optional, d. h. ein Kalkül kann auch ganz ohne Axiome auskommen, wenn er ausreichend viele bzw. mächtige Schlussregeln hat. Axiomfreie Kalküle sind zum Beispiel die Systeme natürlichen Schließens oder Baumkalküle.
Hier soll exemplarisch ein axiomatischer Kalkül gezeigt werden, und zwar jener, den Whitehead und Russell in ihren 1910–1913 entstandenen Principia Mathematica vorstellten. Der Principia Mathematica-Kalkül für die Aussagenlogik umfasst die folgenden Axiome (von denen das vierte redundant, d. h. nicht unbedingt erforderlich, weil aus den anderen Axiomen herleitbar ist):
Um aus diesen Axiomen auch solche gültigen Sätze herleiten zu können, die andere als die in den Axiomen vorkommende Junktoren enthalten, werden diese durch folgende Festlegung auf die vorhandenen Junktoren zurückgeführt:
Alternativ zu – wie hier – konkreten Axiomen kann man auch Axiomenschemata angeben, in welchem Fall man auch ohne Substitutionsregel auskommt. Interpretiert man die obigen Axiome als Axiomenschemata, dann stünde z. B. das erste Axiomenschema,
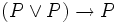 , für unendlich viele Axiome, nämlich alle Ersetzungsinstanzen dieses Schemas.
, für unendlich viele Axiome, nämlich alle Ersetzungsinstanzen dieses Schemas.Herleitung und Beweis
- Hauptartikel: Ableitung (Logik)
Eine Herleitung ist eine Liste von aufsteigend nummerierten Sätzen, die mit einer oder mehreren Annahmen (den Prämissen der Herleitung) oder Axiomen beginnt. Alle auf diese folgenden Sätze sind entweder ebenfalls Axiome (bei manchen Kalkülen sind auch weitere Annahmen zulässig) oder sind aus einer oder mehreren der vorangehenden Zeilen durch Anwendung von Schlussregeln entstanden. Der letzte Satz in der Liste ist die Konklusion der Herleitung.
Eine Herleitung ohne Prämissen heißt Beweis. Oft werden aber die Wörter „Herleitung“ und „Beweis“ synonym gebraucht.
Wenn es gelingt, aus einer Menge von Annahmen (Prämissen) Δ eine Konklusion P herzuleiten, dann schreibt man auch
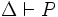 .
.Gelingt es, einen Satz P ohne die Verwendung von Annahmen herzuleiten (zu beweisen), dann schreibt man auch:
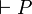 . In diesem Fall wird P Theorem genannt.
. In diesem Fall wird P Theorem genannt.Das Zeichen
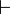 geht auf die Begriffsschrift zurück, jenes Werk, in dem Gottlob Frege 1879 die erste Formalisierung der Prädikatenlogik angegeben hat.
geht auf die Begriffsschrift zurück, jenes Werk, in dem Gottlob Frege 1879 die erste Formalisierung der Prädikatenlogik angegeben hat.In der klassischen Aussagenlogik wählt man die Schlussregeln so, dass sich mit ihrer Hilfe alle gültigen Argumente (und nur gültige Argumente) herleiten lassen; die Frage der Gültigkeit wird im folgenden Abschnitt, „Semantik“, behandelt.
Semantik
Außerhalb der Logik bezeichnet Semantik ein Forschungsgebiet, das sich mit der Bedeutung von Sprache und deren Teilen befasst. Oft wird auch das Wort Semantik gleichbedeutend mit dem Wort Bedeutung verwendet.
Auch innerhalb der Logik geht es bei Semantik um Bedeutung: Darum nämlich, den Ausdrücken einer formalen Sprache – zum Beispiel der hier behandelten Sprache der Aussagenlogik – eine Bedeutung zuzuordnen. In der Logik wird auch das meist sehr formal unternommen.
Im Zentrum der (formalen) Semantik steht eine Auswertungsfunktion (andere Bezeichnungen lauten Bewertungsfunktion, Denotationsfunktion, Wahrheitswertefunktion), die den Formeln der logischen Sprache eine Bedeutung zuordnet. Formal gesprochen ist die Auswertungsfunktion eine Abbildung von der Menge der Formeln der Sprache in die Menge der Wahrheitswerte. Oft wird die Auswertungsfunktion mit dem Großbuchstaben V bezeichnet.
In der klassischen Aussagenlogik ist die Auswertungsfunktion sehr einfach: Das Prinzip der Zweiwertigkeit fordert, dass sie für jede zu bewertende Formel genau einen von genau zwei Wahrheitswerten liefern muss; und das Prinzip der Extensionalität fordert, dass die Bewertungsfunktion beim Bewerten eines komplexen Satzes nur die Bewertung von dessen Teilsätzen berücksichtigen muss.
Jedem Atom, also jedem Satzbuchstaben (Atom) wird durch Festsetzung ein Wahrheitswert zugeordnet. Man sagt: Die Atome werden interpretiert. Es wird also z. B. festgelegt dass P0 wahr ist, dass P1 falsch ist und dass P2 ebenfalls falsch ist. Damit ist der Bewertung der Bausteine der logischen Sprache Genüge getan. Formal ist eine solche Bewertung – Interpretation genannt und oft mit dem Kleinbuchstaben v bezeichnet – eine Funktion im mathematischen Sinn, d. h. eine Abbildung von der Menge der Atome in die Menge der Wahrheitswerte.
Wenn die Auswertungsfunktion V auf ein Atom angewandt wird, d. h. wenn sie ein Atom bewerten soll, liefert sie die Interpretation dieses Atoms im Sinn des obigen Absatzes. Mit anderen Worten, sie liefert den Wert, den die Bewertung v dem Atom zuordnet.
Um die zusammengesetzten Formeln bewerten zu können, muss für jeden Junktor definiert werden, welchen Wahrheitswert die Bewertungsfunktion für die unterschiedlichen Wahrheitswertkombinationen liefert, den seine Argumente annehmen können. In der klassischen Aussagenlogik geschieht das meist mittels Wahrheitstabellen, weil es nur überschaubar wenige Möglichkeiten gibt.
Der einstellige Junktor ¬, die Negation, ist in der klassischen Aussagenlogik so definiert, dass er den Wahrheitswert seines Arguments ins Gegenteil umkehrt, also „verneint“: Ist die Bewertung einer Formel X wahr, dann liefert die Bewertungsfunktion für ¬X falsch; wird aber X falsch bewertet, dann liefert die Bewertungsfunktion für ¬X wahr. Die Wahrheitstabelle sieht folgt aus:
a Negation
¬ aw f f w Die Wahrheitswertverläufe der verwendeten zweistelligen Konnektive sind in der klassischen Aussagenlogik wie folgt definiert:
a b Konjunktion
a ∧ bDisjunktion
a ∨ bmateriale Implikation
Konditional
a → bBikonditional
a ↔ bw w w w w w w f f w f f f w f w w f f f f f w w Allgemein gibt es für die klassische Aussagenlogik vier einstellige und sechzehn zweistellige Junktoren. Die hier behandelte logische Sprache beschränkt sich nur deshalb auf die Junktoren ¬, ∧, ∨, → und ↔, weil diese am gebräuchlichsten sind und weil sie auch inhaltlich noch am ehesten aus der Alltagssprache bekannt sind. Aus formaler Sicht ist die einzige Bedingung, die man bei der Wahl von Junktoren erfüllen möchte, die, dass sich mit den gewählten Junktoren auch alle anderen theoretisch möglichen Junktoren ausdrücken lassen; man sagt: Dass die Menge der gewählten Junktoren funktional vollständig ist. Diese Anforderung ist bei der hier getroffenen Wahl erfüllt.
Näheres zur Frage, wieviele und welche Junktoren es gibt und wie viele Junktoren man benötigt, um funktionale Vollständigkeit zu erreichen, ist im Kapitel Junktor beschrieben.
Semantische Gültigkeit, Tautologien
Semantische Gültigkeit ist eine Eigenschaft von Formeln oder von Argumenten. (Ein Argument ist die Behauptung, dass aus einigen Aussagen – den Prämissen – eine bestimmte Aussage – die Konklusion – folgt.)
Eine Formel der aussagenlogischen Sprache heißt genau dann semantisch gültig, wenn die Formel unter allen Interpretationen – d. h. unter allen Zuordnungen von Wahrheitswerten zu den in ihr vorkommenden Atomen – wahr ist; wenn sie sozusagen allgemeingültig ist; mit anderen Worten: Wenn die Wahrheitstabelle für diese Aussage in jeder Zeile das Ergebnis wahr zeigt. Man nennt semantisch gültige Formeln auch Tautologien und schreibt, wenn
 eine Tautologie ist, formal wie folgt:
eine Tautologie ist, formal wie folgt:Ein Argument heißt genau dann semantisch gültig, wenn unter der Voraussetzung, dass alle Prämissen wahr sind, auch die Konklusion wahr ist. In der Formulierung von Gottfried Wilhelm Leibniz: Aus Wahrem folgt nur Wahres. Diese Definition muss natürlich ebenfalls formal gefasst werden, und das geschieht wie folgt: Ein Argument ist genau dann semantisch gültig, wenn alle Zuordnungen von Wahrheitswerten zu den in Prämissen und Konklusion vorkommenden Atomen, unter denen die Bewertungsfunktion für alle Prämissen den Wert wahr liefert, auch für die Konklusion den Wert wahr liefert.
Um auszudrücken, dass aus einer Menge Δ von Formeln (der Prämissenmenge) eine Formel
 (die Konklusion) semantisch folgt, schreibt man formal wie folgt:
(die Konklusion) semantisch folgt, schreibt man formal wie folgt:Beachte die graphische Ähnlichkeit und die inhaltliche Verschiedenheit zwischen
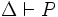 (Kapitel „Herleitung und Beweis“) und
(Kapitel „Herleitung und Beweis“) und 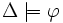 : Die erste Formulierung –
: Die erste Formulierung – 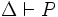 – drückt die syntaktische Gültigkeit des Arguments aus, sagt also, dass aus den Formeln in Δ mit den Schlussregeln des gewählten Kalküls die Formel
– drückt die syntaktische Gültigkeit des Arguments aus, sagt also, dass aus den Formeln in Δ mit den Schlussregeln des gewählten Kalküls die Formel  hergeleitet werden kann.
hergeleitet werden kann. 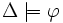 hingegen behauptet die semantische Gültigkeit, die in der klassischen Aussagenlogik wie in den vorangegangenen Absätzen als das Leibniz'sche Aus Wahrem folgt nur Wahres definiert ist.
hingegen behauptet die semantische Gültigkeit, die in der klassischen Aussagenlogik wie in den vorangegangenen Absätzen als das Leibniz'sche Aus Wahrem folgt nur Wahres definiert ist.Siehe auch: Entscheidungsverfahren (klassische Aussagenlogik)
Wichtige semantische Eigenschaften: Erfüllbarkeit, Widerlegbarkeit und Unerfüllbarkeit
Neben der Eigenschaft der Gültigkeit (Allgemeingültigkeit) gibt es einige andere wichtige Eigenschaften: Erfüllbarkeit, Widerlegbarkeit und Unerfüllbarkeit. Im Gegensatz zur Gültigkeit, die Eigenschaft von Formeln oder von Argumenten sein kann, sind Erfüllbarkeit, Widerlegbarkeit und Unerfüllbarkeit Eigenschaften von Sätzen oder von Satzmengen.
- Eine Formel heißt erfüllbar, wenn es mindestens eine Interpretation der in ihr vorkommenden Atome (Satzbuchstaben) gibt, unter der die Formel wahr ist.
- Eine Formel heißt widerlegbar, wenn es mindestens eine Interpretation der in ihr vorkommenden Atome gibt, unter der die Formel falsch ist.
- Eine Formel heißt unerfüllbar, wenn sie unter allen Interpretationen der in ihr vorkommenden Satzbuchstaben falsch ist.
- Eine Formelmenge heißt erfüllbar, wenn alle in ihr enthaltenen Formeln erfüllbar sind.
Die Frage, ob eine Formel (oder eine Formelmenge) eine der genannten Eigenschaften hat, ist ebenso wie die Frage, ob eine Formel allgemeingültig, d. h. eine Tautologie ist, für allgemeine Formeln nicht effizient lösbar: Zwar ist die Wahrheitstafel ein Entscheidungsverfahren für jede dieser Fragen, doch umfasst eine Wahrheitstafel für eine Aussage bzw. eine Aussagemenge in n Atomen 2n Zeilen; das Wahrheitstafelverfahren ist nichts anderes als ein Brute-Force-Verfahren.
Jede dieser Fragestellungen kann auf die Frage zurückgeführt werden, ob eine bestimmte Formel erfüllbar ist:
- Eine Formel
 ist genau dann eine Tautologie, wenn
ist genau dann eine Tautologie, wenn 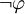 unerfüllbar ist.
unerfüllbar ist. - Eine Formel
 ist genau dann widerlegbar, wenn
ist genau dann widerlegbar, wenn 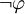 erfüllbar ist.
erfüllbar ist.
Die Frage, ob eine Aussage erfüllbar ist, wird Erfüllbarkeitsproblem oder SAT-Problem (nach dem englischen Wort für Erfüllbarkeit, satisfiability) genannt. Das SAT-Problem spielt eine wichtige Rolle in der theoretischen Informatik und Komplexitätstheorie. Das Erfüllbarkeitsproblem für allgemeine (beliebige) Formeln ist NP-vollständig, d. h. (unter der Voraussetzung, dass P ungleich NP) nicht in polynomialer Laufzeit lösbar.
Für bestimmte echte Teilmengen der Formeln der aussagenlogischen Sprache ist das SAT-Problem dennoch schneller, d. h. in polynomial beschränkter Rechenzeit lösbar. Eine solche Teilmenge sind die Horn-Formeln, das sind Konjunktionen von Disjunktionen, deren Disjunkte verneinte oder unverneinte Atome sind, wobei innerhalb einer solchen Disjunktion allerdings höchstens ein Atom unverneint sein darf.
Algebraische Sicht
Wenn man die Semantik betrachtet, die hier für die klassische Aussagenlogik aufgestellt wurde, dann erkennt man gewisse Gesetzmäßigkeiten. Wird z. B. die Auswertungsfunktion auf eine Aussage der Form X ∧ W angewendet, wobei W eine beliebige wahre Aussage sein soll, dann stellt man fest, dass die Auswertungsfunktion für X ∧ W immer den Wahrheitswert wahr liefert, wenn V(X)=wahr ist (das heißt V(X∧W)=V(X)). Von der Struktur her gleichwertige Gesetzmäßigkeiten gelten auch in anderen Semantiken, auch in solchen, die für ganz andere, nichtlogische Systeme aufgestellt werden. Für die Arithmetik gilt z. B., dass die dortige Bewertungsfunktion (hier VArithmetik genannt) für einen Ausdruck der Form X + Y immer den Wert von X liefert, sofern der Wert von Y null ist: VArithmetik(X+Y)=VArithmetik(X), wenn VArithmetik(Y) = null ist.
Eine formale Wissenschaft, die solche strukturellen Gesetzmäßigkeiten untersucht, ist die abstrakte Algebra (meist Teilgebiet der Mathematik, aber auch der Informatik). In der abstrakten Algebra wird zum Beispiel untersucht, für welche Verknüpfungen es ein neutrales Element gibt, d. h. ein Element N, das für eine Verknüpfung op dazu führt, dass (für beliebiges X) gilt: X op N = X. So würde man aus algebraischer Sicht sagen, dass es für die klassische aussagenlogische Konjunktion genau ein neutrales Element gibt, nämlich wahr, und dass es für die Addition in der Arithmetik ebenfalls genau ein neutrales Element gibt, nämlich die Zahl Null. Nur am Rande sei erwähnt, dass es auch für andere Junktoren neutrale Elemente gibt; das neutrale Element für die Disjunktion ist falsch: V(X ∨ F) = V(X), wenn V(F)=falsch ist.
Die formale Algebra betrachtet formale Semantiken rein nach ihren strukturellen Eigenschaften. Sind diese identisch, dann besteht zwischen ihnen aus algebraischer Sicht kein Unterschied. Aus algebraischer Sicht, genauer: Aus Sicht der formalen Algebra ist die Semantik für die klassische Aussagenlogik eine zweiwertige Boolesche Algebra. Andere formale Systeme, deren Semantiken jeweils eine Boolesche Algebra bilden, sind die Schaltalgebra und die elementare Mengenlehre. Aus algebraischer Sicht besteht daher zwischen diesen Disziplinen kein Unterschied.
Metatheorie
In der Metatheorie werden die Eigenschaften von logischen Systemen untersucht: Das logische System ist in der Metatheorie der Untersuchungsgegenstand.
Eine metatheoretische Fragestellung ist zum Beispiel die, ob in einem Kalkül ein Widerspruch hergeleitet werden kann.
Der vorliegende Abschnitt soll einige wichtige metatheoretische Fragestellungen aus dem Blickwinkel der Aussagenlogik betrachten.
- Konsistenz
- Ein Kalkül wird genau dann konsistent genannt, wenn es unmöglich ist, mit Hilfe seiner Axiome und Regeln einen Widerspruch herzuleiten, d. h. eine Aussage der Form P ∧ ¬ P (z. B. „Hugo ist groß, und Hugo ist nicht groß“). Für einen Kalkül, der in der Aussagenlogik verwendet werden soll, ist das eine Mindestanforderung.
- Ist es in einem Kalkül möglich, einen Widerspruch herzuleiten, dann wird der Kalkül inkonsistent genannt.
- Es gibt formale Systeme, in denen solch ein Widerspruch hergeleitet werden kann, die aber durchaus sinnvoll sind. Für solche Systeme wird ein anderer Konsistenzbegriff verwendet: Ein Kalkül ist konsistent, wenn in ihm nicht alle Formeln herleitbar sind (siehe parakonsistente Logik).
- Es lässt sich leicht zeigen, dass für die klassische Logik die beiden Konsistenzbegriffe zusammenfallen: In der klassischen Logik lässt sich aus einem Widerspruch jeder beliebige Satz herleiten (dieser Sachverhalt wird Ex falso quodlibet genannt), d. h. wenn ein klassischer Kalkül auch nur einen Widerspruch herleiten könnte, also im ersten Sinn inkonsistent wäre, dann könnte er jede Aussage herleiten, wäre also im zweiten Sinn inkonsistent. Wenn umgekehrt ein Kalkül inkonsistent im zweiten Sinn ist, also in ihm jede Aussage herleitbar ist, dann ist insbesondere auch jeder Widerspruch herleitbar und ist er auch inkonsistent im ersten Sinn.
- Korrektheit
- Ein Kalkül heißt genau dann korrekt (semantisch korrekt), wenn in ihm nur solche Formeln hergeleitet werden können, die auch semantisch gültig sind. Für die klassische Aussagenlogik bedeutet das einfacher: Ein Kalkül ist genau dann korrekt, wenn in ihm nur Tautologien bewiesen und nur gültige Argumente hergeleitet werden können.
- Ist es in einem aussagenlogischen Kalkül möglich, mindestens ein ungültiges Argument herzuleiten oder mindestens eine Formel zu beweisen, die keine Tautologie ist, dann ist der Kalkül inkorrekt.
- Vollständigkeit
- Vollständig (semantisch vollständig) heißt ein Kalkül genau dann, wenn in ihm alle semantisch gültigen Formeln hergeleitet werden können; für die Klassische Aussagenlogik: Wenn in ihm alle Tautologien hergeleitet werden können.
- Adäquatheit
- Ein Kalkül heißt genau dann im Hinblick auf eine spezielle Semantik adäquat, wenn er (semantisch) korrekt und (semantisch) vollständig ist.
Ein metatheoretisches Resultat ist zum Beispiel die Feststellung, dass alle korrekten Kalküle auch konsistent sind. Ein anderes metatheoretisches Resultat ist die Feststellung, dass ein konsistenter Kalkül nicht automatisch korrekt sein muss: Es ist ohne weiteres möglich, einen Kalkül aufzustellen, in dem zwar kein Widerspruch hergeleitet werden kann, indem aber z. B. die nicht allgemeingültige Aussage der Form „A ∨ B“ hergeleitet werden kann. Ein solcher Kalkül wäre aus ersterem Grund konsistent, aus letzterem Grund aber nicht korrekt.
Ein weiteres, sehr einfaches Resultat ist die Feststellung, dass ein vollständiger Kalkül nicht automatisch auch korrekt oder nur konsistent sein muss. Das einfachste Beispiel wäre ein Kalkül, in dem jede Formel der aussagenlogischen Sprache herleitbar ist. Da jede Formel herleitbar ist, sind alle Tautologien herleitbar, die ja Formeln sind: Das macht den Kalkül vollständig. Da aber jede Formel herleitbar ist, ist insbesondere auch die Formel P0 ∧ ¬ P0 und die Formel A ∨ B herleitbar: Ersteres macht den Kalkül inkonsistent, letzteres inkorrekt.
Das Ideal, das ein Kalkül erfüllen sollte, ist Korrektheit und Vollständigkeit: Wenn das der Fall ist, dann ist er der ideale Kalkül für ein logisches System, weil er alle semantisch gültigen Sätze (und nur diese) herleiten kann. So sind die beiden Fragen, ob ein konkreter Kalkül korrekt und/oder vollständig ist und ob es für ein bestimmtes logisches System überhaupt möglich ist, einen korrekten und vollständigen Kalkül anzugeben, zwei besonders wichtige metatheoretische Fragestellungen.
Abgrenzung und Philosophie
Die klassische Aussagenlogik, wie sie hier ausgeführt wurde, ist ein formales logisches System. Als solches ist sie eines unter vielen, die aus formaler Sicht gleichwertig nebeneinander stehen und die ganz bestimmte Eigenschaften haben: Die meisten sind konsistent, die meisten sind korrekt, etliche sind vollständig, und einige sind sogar entscheidbar. Aus formaler Sicht stehen die logischen Systeme in keinem Konkurrenzverhalten hinsichtlich Wahrheit oder Richtigkeit.
Von formalen, innerlogischen Fragen klar unterschieden sind außerlogische Fragen: Solche nach der Nützlichkeit (Anwendbarkeit) einzelner Systeme für einen bestimmten Zweck und solche nach dem philosophischen, speziell metaphysischen Status einzelner Systeme.
Die Nützlichkeitserwägung ist die einfachere, bezüglich deren Meinungsunterschiede weniger tiefgehend bzw. weniger schwerwiegend sind. Klassische Aussagenlogik zum Beispiel bewährt sich in der Beschreibung elektronischer Schaltungen (Schaltalgebra) oder zur Formulierung und Vereinfachung logischer Ausdrücke in Programmiersprachen. Prädikatenlogik wird gerne angewandt, wenn es darum geht, Faktenwissen zu formalisieren und automatisiert Schlüsse daraus zu ziehen, wie das unter anderem im Rahmen der Programmiersprache Prolog geschieht. Fuzzy-Logiken, nonmonotone, mehrwertige und auch parakonsistente Logiken sind hochwillkommen, wenn es darum geht, mit Wissensbeständen umzugehen, in denen Aussagen mit unterschiedlich starkem Gewissheitsgrad oder gar einander widersprechende Aussagen abgelegt werden sollen und dennoch sinnvolle Schlüsse aus dem Gesamtbestand gezogen werden sollen. Auch wenn es je nach Anwendungsfall sehr große Meinungsunterschiede geben kann, welches logisches System besser geeignet ist, ist die Natur des Problems für alle Beteiligten unmittelbar und in gleicher Weise greifbar. Einzelwissenschaftliche Überlegungen und Fragestellungen spielen sich überwiegend in diesem Bereich ab.
(Noch) kontroverser als solche pragmatischen Überlegungen sind Fragestellungen philosophischer und metaphysischer Natur. Geradezu paradigmatisch ist die Frage, „welches logische System richtig ist“, wobei „richtig“ hier gemeint ist als: Welches logische System nicht nur einen Teilaspekt der Wirklichkeit modellhaft vereinfacht, sondern die Wirklichkeit, das Sein als Ganzes adäquat beschreibt. Zu dieser Fragestellung gibt es viele unterschiedliche Meinungen einschließlich der vom philosophischen Positivismus eingeführten Meinung, dass die Fragestellung als Ganzes sinnlos ist.
In den Bereich metaphysischer Fragestellungen fällt auch die Frage, ob es so etwas wie ein metaphysisches Prinzip der Zweiwertigkeit gebe, ob also Aussagen über die Wirklichkeit durchgehend ins Schema wahr/falsch passen oder nicht. Diese Frage ist unabhängig von der Frage, ob die Beschäftigung mit zwei- oder mehrwertigen Logiken praktisch sinnvoll ist: Selbst wenn ein metaphysisches Prinzip der Zweiwertigkeit herrscht, könnte man anwendungspraktisch mehrwertige Logiken nützen, etwa dazu, epistemische Sachverhalte zu fassen, zum Beispiel aus Aussagen zu schließen, die zwar metaphysisch wahr oder falsch sind, von denen aber nicht oder noch nicht bekannt ist, welches von beidem der Fall ist. Umgekehrt kann man auch dann, wenn ein solches metaphysisches Prinzip nicht gilt, zweiwertige Logik wegen ihrer Einfachheit für solche Anwendungen bevorzugen, bei denen nur mit solchen Sätzen umgegangen werden muss, die tatsächlich wahr oder falsch sind.
Die Frage nach einem metaphysischen Prinzip der Zweiwertigkeit ist wie die meisten metaphysischen Fragen nicht endgültig zufriedenstellend beantwortet. Ein früher Einwand gegen ein solches Prinzip, den Aristoteles zur Diskussion stellte, war das Thema der Aussagen über zukünftige Sachverhalte („Morgen wird es regnen“). Wenn Aussagen über Zukünftiges schon heute wahr oder falsch wären, so wird argumentiert, dann müsse die Zukunft bis ins letzte Detail vorbestimmt sein. Ein anderer Einwand, der vorgebracht wird, ist, dass es Aussagen gibt, deren Wahrheit praktisch oder theoretisch nicht festgestellt werden kann – zum Beispiel lässt sich die Wahrheit von „Der Rasen vor dem weißen Haus bestand am 1. Februar 1870 aus genau 6.120.375,4 Grashalmen“ einfach nicht feststellen.
Befürworter eines metaphysischen Zweiwertigkeitsprinzips berufen sich oft auf das Verhalten von Metatheoretikern, also von Mathematikern oder Logikern, die Aussagen über formale Systeme treffen: Egal wie mehrwertig oder nichtklassisch das untersuchte System ist, die dabei getroffenen Metavermutungen, Metabehauptungen und Metafeststellungen sind immer zweiwertig: Ein Kalkül, auch ein parakonsistenter oder nonmonotoner, wird immer als entweder konsistent oder inkonsistent betrachtet, und ein logisches System ist immer entweder korrekt oder inkorrekt, vollständig oder nicht vollständig, entscheidbar oder unentscheidbar, niemals „ein bisschen“ von beidem. Befürworter deuten das als Hinweis darauf, dass es in der Wirklichkeit tatsächlich eine strenge Unterscheidung nach wahr und falsch gebe oder dass es zumindest sinnvoll ist, eine solche anzunehmen.
Eine andere philosophische Fragestellung ist die nach dem metaphysischen Status des Untersuchungsgegenstands der Logik, also danach, was logische Systeme, Kalküle, Wahrheitswerte eigentlich „sind“.
Der platonistische Standpunkt besteht darin, dass die in der Logik verwendeten Zeichen und Konstrukte eine außerlogische Bedeutung haben, dass sie Namen für real existierende (wenn auch natürlich nicht-physikalische) Gegenstände sind. In diesem Sinn gäbe es so etwas wie das Wahre und das Falsche, abstrakte Gegenstände, die von den Zeichen „wahr“ und „falsch“ benannt werden.
Der Gegenpol zum Platonismus wäre der Nominalismus, der Existenz nur den Zeichen zuspricht, die in der Logik manipuliert werden. Gegenstand der Logik sind Zeichen, und die Tätigkeit der Logiker ist die Manipulation von Zeichen. Die Zeichen bezeichnen aber nichts, so etwas wie das Wahre oder das Falsche gibt es also nicht. Im Grundlagenstreit der Mathematik entspräche der nominalistischen Position die formalistische Richtung.
Eine Mittelstellung nähme der philosophische Konstruktivismus ein, demzufolge die Zeichen zwar keine unabhängig existierenden Gegenstände bezeichnen, durch den Umgang mit den Zeichen aber Gegenstände konstruiert werden.
Siehe auch
- Elementaraussage
- Existential Graphs nach Peirce
- Prädikatenlogik
- Wahrheitstabelle
- Schlussregel
- Boolesche Funktion
- Wahrheitswertefunktion
- Formelsammlung Logik
Literatur
Bemerkungen zur Einführungsliteratur
Die meisten Werke, die klassische Aussagenlogik behandeln, behandeln zusätzlich zumindest ein weiteres logisches System, meist klassische Prädikatenlogik (formal eine echte Erweiterung der Aussagenlogik). Es wird versucht, an dieser Stelle in erster Linie solche Werke anzugeben, die eine saubere Trennung zwischen Aussagenlogik und den weiteren behandelten Systemen aufweisen.
Auch mit dieser Einschränkung ist die Einführungsliteratur zur Aussagenlogik sehr zahlreich und die Liste hier eine Auswahl. Insofern man eine Einteilung vornehmen möchte, entdeckt man vor allem folgende Unterschiede:
- Es gibt Werke, die einen syntaktischen Schwerpunkt haben, also sich in erster Linie mit dem Herleiten von Theoremen und Beweisen innerhalb eines Kalküls befassen und erst später eine formale Semantik vorstellen. Ein typischer Vertreter ist Lemmon 1965. Andere Werke haben einen semantischen Zugang, d. h. motivieren ihr Vorgehen sehr stark semantisch. Ein leicht zu lesendes, aber sehr instruktives Buch ist Hodges 1977.
- Hinsichtlich der verwendeten Kalküle unterscheiden sich die Einführungsbücher, vielfach aber weniger stark, als man erwarten könnte. Die meisten Einführungen verwenden Regelkalküle (Schlussregelkalküle), d. h. Kalküle, die ohne Axiome auskommen, dafür aber etliche Schlussregeln umfassen. Davon abweichend sind vor allem radikaler semantisch orientierte Einführungen, hier Hodges 1977, der einen Baumkalkül verwendet. Ebenfalls abweichend sind Einführungswerke, die sich an Fachleser/innen aus anderen formalen Disziplinen richten, z. B. aus der Informatik. Solche Werke tragen oft den Zusatz „für Informatiker“ im Titel (ein Beispiel ist Schöning 1995) und stellen meist axiomatische Kalküle dar, oft auch Kalküle, die fürs maschinelle Schließen von Bedeutung sind, z. B. Resolutionskalküle.
- Und schließlich gibt es eine gewisse Bandbreite hinsichtlich des Zielpublikums, an das sich die Einführungsliteratur richtet. Solche, die sich an Mathematiker oder Informatiker richtet, ist für interessierte Laien normalerweise nicht geeignet oder sehr mühsam. In der folgenden Literaturliste sollen in erster Linie Werke genannt werden, die keine formalen Vorauskenntnisse erfordern, bzw. soll Abweichendes ausdrücklich erwähnt werden.
Liste von Einführungsliteratur
- Jon Barwise, John Etchemendy: Sprache, Beweis und Logik. Band 1. Aussagen- und Prädikatenlogik, Paderborn: Mentis 2005 ISBN 3-89785-440-6 – Band 2 noch nicht erschienen
- Jon Barwise, John Etchemendy: The Language of First Order Logic, Stanford: CSLI 1991 (=CSLI Lecture Notes; 23) ISBN 0-937073-74-1 – in englischer Sprache, syntaktischer Zugang
- Ansgar Beckermann: Einführung in die Logik ISBN 3-11-017965-2
- Wolfgang Detel, Grundkurs Philosophie, Band 1. Logik, Stuttgart: Reclam 2007, ISBN 978-3-15-018468-4 (Universal-Bibliothek, Nr. 18468).
- Wilfrid Hodges: Logic, London: Penguin 1977, 2. Aufl. 2001 ISBN 0-14-100314-6 – semantisch motiviertes Einführungsbuch, das keine Vorkenntnisse voraussetzt; in englischer Sprache
- Paul Hoyningen-Huene: Formale Logik. Eine philosophische Einführung, Stuttgart: Reclam 2002 ISBN 3-15-009692-8
- Donald Kalish, Richard Montague, Gary Mar: Logic. Techniques of Formal Reasoning, New York: Harcourt Brace Jovanovich 1964, 2. Aufl. 1980 ISBN 0-15-551181-5 – in englischer Sprache
- E. J. Lemmon: Beginning Logic, London: Chapman and Hall London 1965, 2. Aufl. 1987 ISBN 0-412-38090-0 – kompakte, syntaktisch motivierte Einführung in englischer Sprache
- Benson Mates: Elementare Logik. Prädikatenlogik der ersten Stufe mit Identität, Göttingen: Vandenhoeck & Ruprecht, 2. Aufl. 1978 (=Moderne Mathematik in elementarer Darstellung; 9) ISBN 3-525-40541-3 – syntaktisch motivierte Einführung in deutscher Übersetzung
- Schöning, Uwe: Logik für Informatiker, Heidelberg; Berlin; Oxford: Spektrum, Akademischer Verlag 1995 ISBN 3-86025-684-X
- Willard Van Orman Quine: Grundzüge der Logik, Frankfurt/Main: Suhrkamp 1969, 6. Aufl. 1988 (=Suhrkamp Taschenbuch Wissenschaft) ISBN 3-518-27665-4 – verwendet eine heute ungebräuchliche und anfangs oft als kompliziert empfundene Notation
- Wesley C. Salmon: Logik, Stuttgart: Reclam 1983 (=Universal-Bibliothek) ISBN 3-15-007996-9
- Tarski, Alfred: Einführung in die mathematische Logik, Göttingen: Vandenhoeck & Ruprecht 1966, 5. Aufl. 1977 (=Moderne Mathematik in elementarer Darstellung; 5) ISBN 3-525-40540-5
Weiterführende Werke in deutscher Sprache
- Karel Berka, Lothar Kreiser: Logik-Texte. Kommentierte Auswahl zur Geschichte der modernen Logik, Berlin: Akademie 4. Aufl. 1986 – druckt (überwiegend in ungekürzter Fassung) einige der Schlüsseltexte der modernen Logik ab und leitet sie jeweils mit einem ausführlichen Kommentar ein. ISBN 3-05-001500-4
- Rüdiger Inhetveen: Logik. Eine dialog-orientierte Einführung. Leipzig 2003 ISBN 3-937219-02-1 – legt eine andere Sichtweise auf Logik zugrunde.
- Lothar Kreiser, Siegfried Gottwald, Werner Stelzner (Hge.): Nichtklassische Logik. Eine Einführung, Berlin: Akademie 2. Aufl. 1990 ISBN 3-05-000274-3 – Einführung in Themen der nichtklassischen Logik mit einer Vielzahl nichtklassischer logischer Systeme und ausführlicher inhaltlicher und auch anwendungsorientierter Überlegungen; das Werk setzt Kenntnisse der klassischen Logik voraus.
Weblinks
- Kevin C. Klement: „Propositional Logic“ in der Internet Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
- Logik für Informatiker (Universität Würzburg)
- Wikibook (englisch) Logik für Informatiker (Universität Koblenz)
- Vorlesungsmitschnitt Mathematik I (Uni Tübingen). Die ersten zwei Stunden handeln ausführlich von Wahrheitstabellen.
Einzelnachweise
- ↑ Karl Dürr: Aussagenlogik im Mittelalter. Erkenntnis, 7, 1937/38, S. 160-168
Wikimedia Foundation.

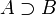
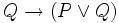
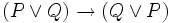
![[P \or (Q \or R)] \rightarrow [Q \or (P \or R)]](/pictures/dewiki/51/30dfc80fb80f29e90a047db313996c6f.png)
![(Q \rightarrow R) \rightarrow [(P \or Q) \rightarrow (P \or R)]](/pictures/dewiki/48/0ddfb1e1a088bbd0a26f560862d96f7a.png)